이진 검색이란?
이진 검색은 검색 알고리즘의 일종으로, 선형 검색(linear search)보다 빠른 알고리즘이다.
그러나, 선형 검색과는 다르게 이진 검색 알고리즘을 사용하려면 배열의 데이터가 정렬(오름차순, 내림차순)되어 있어야 한다. 아래는 이진 검색과 선형 검색의 검색 과정을 비교한 이미지다.
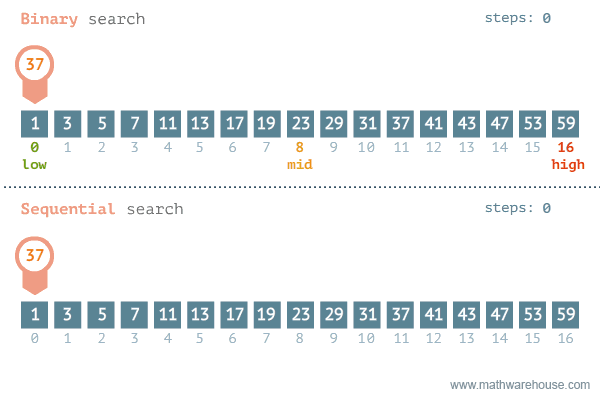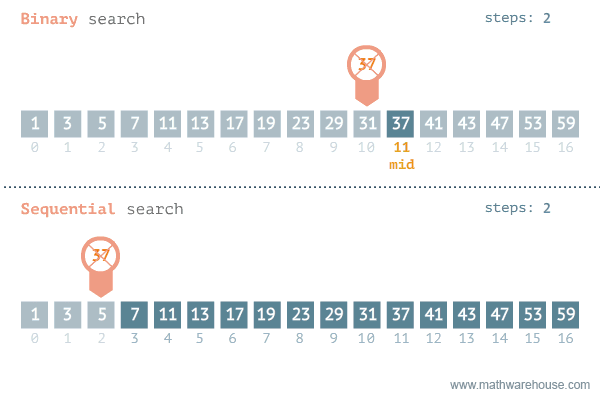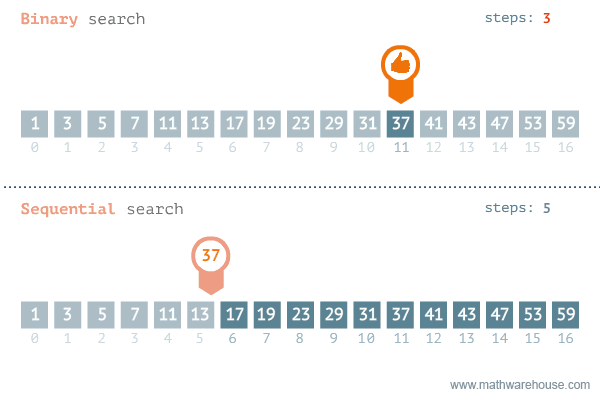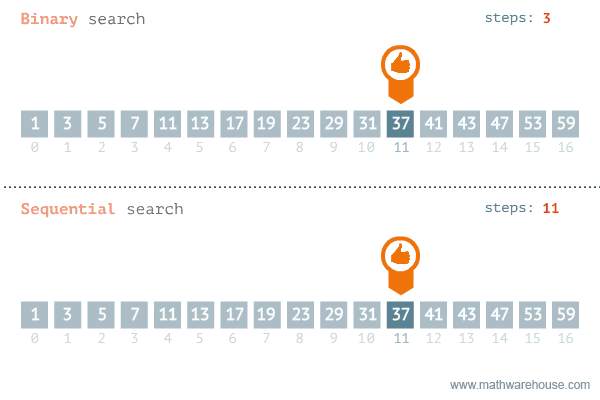index 0부터 N-1까지 순차적으로 key와 비교하는 선형 검색과 비교했을 때 가장 큰 차이점으로는, 배열의 시작(pl)과 끝(pr) 원소를 설정하고 중앙 원소(mid)에는 (pl+pc) // 2의 값을 설정하여 원소 key 를 찾을 때까지 pl과 pr, mid의 위치를 조정한다.
시간 복잡도
먼저, 선형 검색의 시간 복잡도는 O(n)이다. 그 이유는 n에 비례하는 횟수만큼 실행되기 때문이다. n이 점점 커지면 필요한 계산 시간은 n에 비례하여 점점 길어진다. 그에 반해 이진 검색은 O(log n)의 복잡도를 가진다.
시간 복잡도, 공간 복잡도에 대한 자세한 내용은 다음에 다시 다룰 예정이다. 아래 내용만 훑고 넘어가자.
시간 및 공간 복잡도는 클수록 안좋다.
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(n^k) < O(2^n)
<- 작다 --------------------------------------------------------------------크다 ->
예제 코드
# binary search
import sys
from typing import Any, Sequence
def binary_search(a: Sequence, key: Any) -> int:
# Sequence a에서 key와 일치하는 원소를 이진 검색하는 함수
pl = 0
pr = len(a)-1
while True:
mid = (pl + pr) // 2 # 중앙에 있는 원소의 인덱스 설정
if a[mid] == key: # mid에 위치한 원소가 찾고 있는 값과 같다면
return mid # 검색 성공
elif a[mid] < key:
pl = mid + 1 # 검색 범위를 뒤쪽 절반으로 좁힘
else:
pr = mid - 1 # 검색 범위를 앞쪽 절반으로 좁힘
if pl > pr: # pl이 pr보다 커졌다면 반복문을 멈추고
break
return -1 # 검색 실패
if __name__ == '__main__':
print('원소 수 입력 : ')
N = int(sys.stdin.readline())
arr = [None] * N # N개의 None값 배열을 미리 생성
print('<배열 데이터를 오름차순으로 입력하세요>')
print('arr[0]: ', sep="")
arr[0] = int(sys.stdin.readline())
for i in range(1, N):
while True:
print(f'arr[{i}]: ')
arr[i] = int(sys.stdin.readline())
if arr[i] >= arr[i - 1]: # 입력받은 수가 직전 원솟값보다 크면 종료(오름차순)
print("수를 오름차순으로 입력!")
break
print('검색할 값 : ')
key = int(sys.stdin.readline())
idx = binary_search(arr, key)
if idx == -1:
print('해당 원소가 존재하지 않음')
else:
print(f'검색한 값은 arr[{idx}]에 있음')
