[Programmers] 등굣길

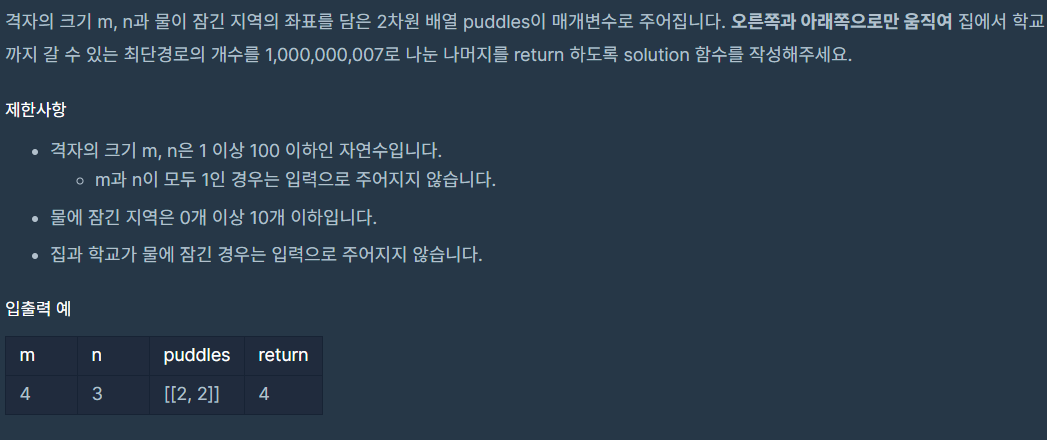
• 문제
  
  

• 코드

#include <string>
#include <vector>

using namespace std;

int solution(int m, int n, vector<vector<int>> puddles) {
    int answer = 0;
    
    int dp[n+1][m+1];
    for(int i=0; i<n+1; i++){
        for(int j=0; j<m+1; j++){
            dp[i][j] = 0;
        }
    }
    
    for(int i=0; i<puddles.size(); i++){
        int x = puddles[i][0];
        int y = puddles[i][1];
        
        dp[y][x] = -1; //웅덩이 -1로 표시
    }
    
    dp[1][0] = 1;

    for(int i=1; i<n+1; i++){
        for(int j=1; j<m+1; j++){
            if(dp[i][j]==-1) dp[i][j] = 0;
            else{
                dp[i][j] = (dp[i][j-1] + dp[i-1][j]) % 1000000007;
            }
        }
    }
 
    answer = dp[n][m];
    return answer;
    
}

• 풀이

- 기본적으로 우측, 아래로만 이동한다면, 갈 수 있는 방법의 수는 좌측칸과 윗칸까지 도달할 수 있는 방법의 합이다.
dp[i][j] = (dp[i][j-1] + dp[i-1][j])

- 인덱스를 넘어가는 것을 방지하여 DP의 크기를 한칸 더 크게 설정하고 1,1부터 값을 채워나가도록 하였다.

- 초기에 모든 칸을 0으로, 웅덩이는 -1로 초기화하고 탐색과정에서 웅덩이일 경우 0으로, 그렇지 않을 경우 점화식을 이용해 방법의 수를 계산하고 업데이트 해주었다.
(탐색을 좌->우 위->아래 순서로 하므로 웅덩이를 0으로 설정해주면 문제없이 점화식의 결과값을 얻을 수 있다.)

- dp[1][0] = 1; 로 dp[1][1] 의 값이 1이되도록 한다.

코드가 정교하지 못한 느낌이 있다. 방법을 알고 있어서 쉽게 해결하였다.