그리디 (Greedy Algorithm)

• 당장 눈 앞에 보이는 최적의 상황만을 쫓는 알고리즘
• 현재 상황에서 가장 좋아보이는(즉, 최적이라고 생각되는) 선택을 반복하여 전체 문제의 최적해를 찾는 알고리즘
• 특징
  • 부분 문제에서의 최적 선택이 전체 문제의 최적 해를 보장해야 한다.(Greedy Choice Property)
  • 이후의 선택에 영향을 미치지 않아야 한다. (Optimal Substructure)
• 대표적인 문제 유형
  • 거스름돈 문제: 최소한의 동전 개수로 거스름돈을 만드는 문제
  • 회의실 배정 문제: 가장 많은 회의를 진행할 수 있도록 선택하는 문제
  • 배낭 문제(Fractional Knapsack): 무게당 가치가 높은 순서대로 담는 문제
• 주의사항
  • 모든 문제에서 최적해를 보장하지 않는다.
    • 동적 프로그래밍(DP)과 비교하여 사용 여부 결정
  • 반례가 없는지 철저히 검토해야 함

그리디 알고리즘은 기본적으로 무조건 큰 경우대로, 무조건 작은 경우대로, 무조건 긴 경우대로, 무조건 짧은 경우대로 등으로 극단적으로 문제에 접근한다는 점에서 정렬(Sort) 기법이 함께 사용되는 경우가 많다. 대표적인 예시로 크루스칼(Kruskal) 알고리즘으로 모든 간선을 정렬한 이후에 짧은 간선부터 연결하는 최소 비용 신장 트리 알고리즘이 있다.

예시: 거스름돈 문제

우리가 흔히 거스름 돈을 줄 때 가장 적은 양의 화폘르 주는 것이 제일 편하다.
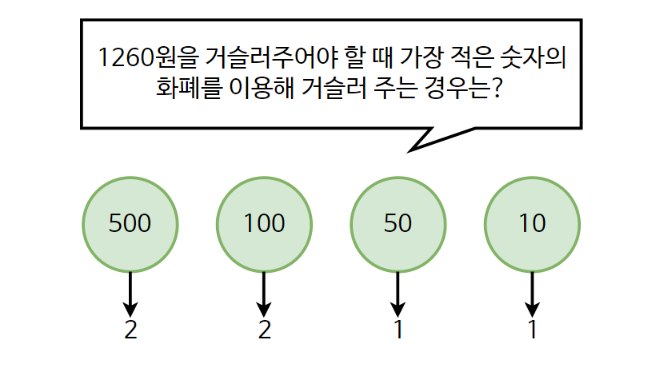
예를들어 1260원을 거슬러주어야 할 때, 500 * 2 + 100 * 2 + 50 * 1 + 10 * 1으로 6개의 동전을 거슬러주면 된다.
이처럼 무조건 큰 화폐 단위를 거슬러 준다는 알고리즘만 지키면 최적의 해를 보장할 수 있다.

💻 코드

public class Main {
    public static void main (String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int result = 0;

        // 그리디 적용: 큰 단위의 동전부터 사용
        result += n / 500;
        n %= 500;
        result += n / 100;
        n %= 100;
        result += n / 50;
        n %= 50;
        result += n / 10;
        n %= 10;

        System.out.println(result);

        scanner.close();
    }
}