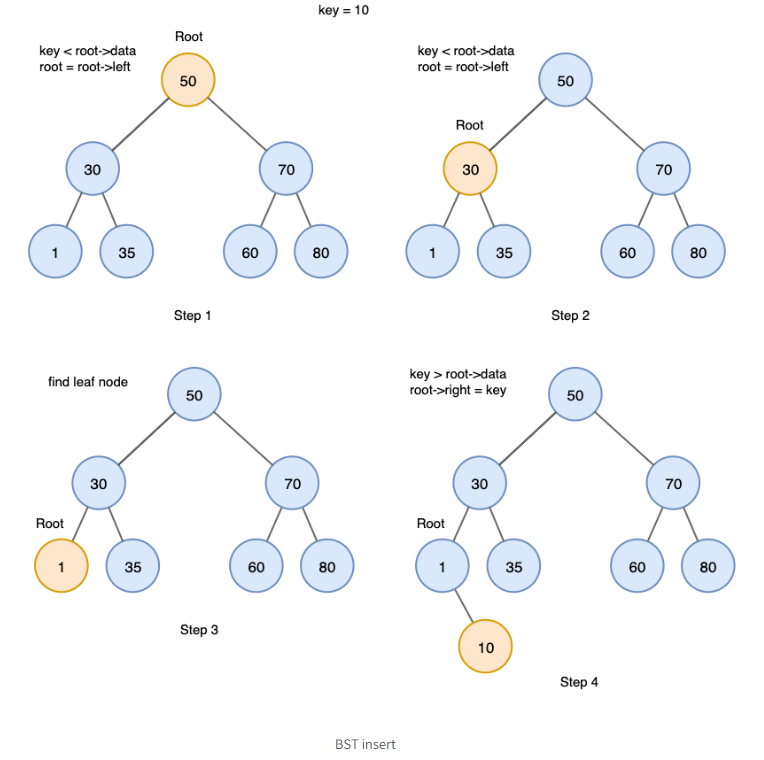
문제
풀이
💻 결과 코드
package common;
public class Solution {
public int rangeSumBST(TreeNode root, int low, int high) {
if (root == null) {
return 0;
}
int sum = 0;
if (root.val >= low && root.val <= high) {
sum += root.val;
}
if (root.val > low) {
sum += rangeSumBST(root.left, low, high);
}
if (root.val < high) {
sum += rangeSumBST(root.right, low, high);
}
return sum;
}
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}TreeNodeint val: 노드의 값을 저장TreeNode left: 왼쪽 노드 자식TreeNode right: 오른쪽 노드 자식
rangeSumBST- 기저조건: 현재 노드가 null인 경우, 더 이상 탐색할 노드가 없으므로 0을 반환한다.

- 현재 노드의 값이 범위에 있는지 확인

- 왼쪽 서브트리 탐색
- 현재의 노드가 low보다 큰 경우, 왼쪽 서브트리의 노드들도 범위에 있을 가능성이 있으므로 왼쪽 서브트리를 재귀적으로 탐색한다.

- 오른쪽 서브트리 탐색
- 현재 노드가 high보다 작은 경우, 오른쪽 서브트리의 노드들도 범위 내에 있을 가능성이 있으므로 오른쪽을 재귀적으로 탐색한다.

- 기저조건: 현재 노드가 null인 경우, 더 이상 탐색할 노드가 없으므로 0을 반환한다.
TreeNode 구조를 입력한 root를 직접 살펴보면서 다양한 방향으로 탐색해보았는데, 리프 노드에서 다시 상위로 올라가는 개념을 시도하면서 시간을 많이 소비했다.. 최종적으로는 재귀적으로 하위 리프로 내려가면서 값의 유무를 분석하는 방식으로 문제가 해결되었다. 평상시 재귀라는 개념이 직관적으로 와닿지 않았는데, 이진트리의 트리구조와 재귀라는 개념을 동시에 살펴보면서 좀 더 입체적으로 이해할 수 있어서 좋았다.
📗이진 탐색 트리(Binary Search Tree, BST)
개요
- 이진 트리는 정렬되지 않은 형태이므로 탐색을 수행하기에 적절하지 않다.
- 이를 위해 이진 트리의 특수한 형태인 이진 탐색 트리가 있으며, 정렬된 형태의 이진트리이고 이는 탐색을 위한 트리로 사용 될 수 있다.
- 즉, 이진 탐색의 개념을 트리 형태의 구조에 접목한 자료구조이다.
- 이진 탐색: 정렬된 데이터의 중간에 위치한 항목을 기준으로 데이터를 두 부분으로 나누어가며 탐색하는 방법
- 이진 탐색 트리의 특징: 트리를 중위순회(Inorder)하면 정렬되어 출력된다.
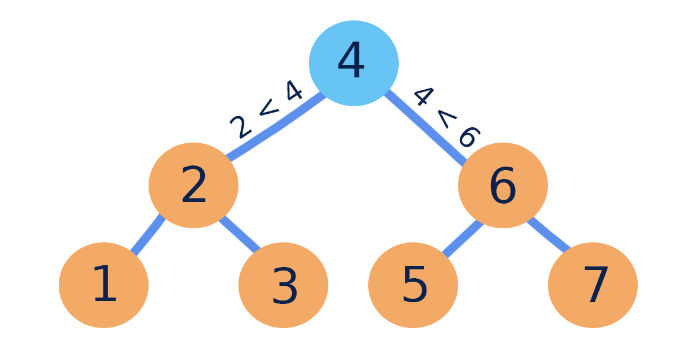
특징
- 각 노드에 값이 있다.
- 값들은 전순서가 있다.
- 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 트리여야 한다.
이진트리의 연산
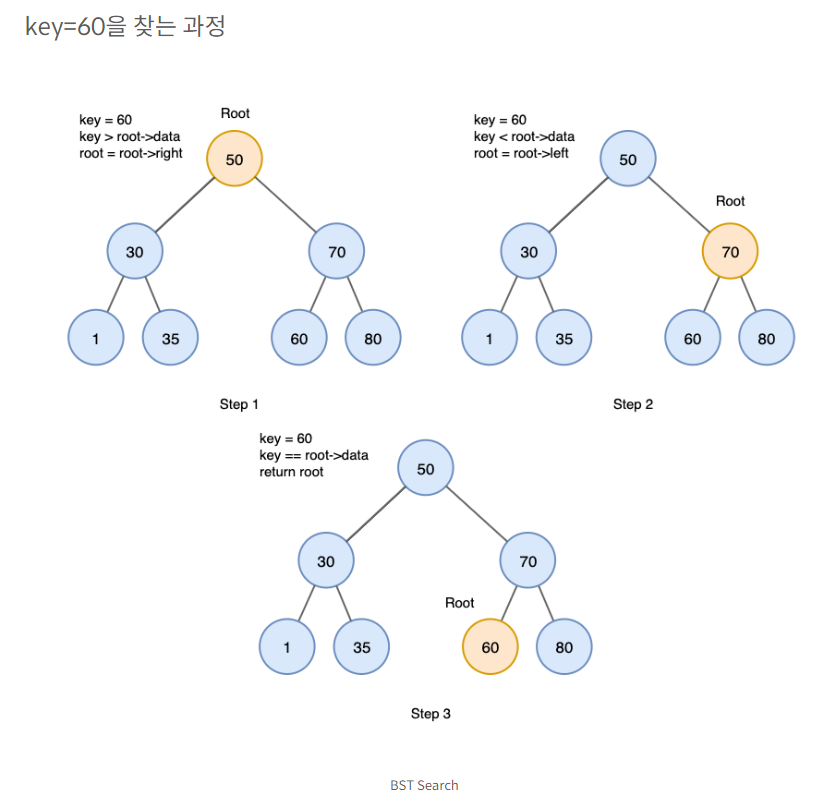
1. 검색 (Search)
이진 탐색 트리에서 특정 요소의 위치를 찾는다.
- 루트에서 시작한다.
- 검색 값을 루트와 비교한다. 루트보다 작으면 왼쪽에 대해 재귀하고 크다면 오른쪽으로 재귀한다.
- 일치하는 값을 찾을 때까지 절차를 반복한다.
- 검색 값이 없으면 null을 반환한다.
2. 삽입 (Insert)
이진 검색트리에 데이터를 삽입하는 작업을 한다. 새 키는 항상 리프노드에 삽입된다.
- Root에서 시작한다.
- 삽입 값을 루트와 비교한다. 루트보다 작으면 왼쪽으로 재귀하고 크다면 오른쪽으로 재귀한다.
- 리프 노드에 도달한 후 노드보다 크다면 오른쪽에 작다면 왼쪽에 삽입한다.