[leetcode] 2824. Count Pairs Whose Sum is Less than Target

bien·2024년 5월 27일

목록 보기

6/14

문제

2824. Count Pairs Whose Sum is Less than Target

풀이

💻 결과 코드

class Solution {
    public int countPairs(List<Integer> nums, int target) {
        int count = 0;

        for (int i = 0; i < nums.size(); i++) {
            for (int j = 0; j < nums.size(); j++) {
                if ((i < j) && nums.get(i) + nums.get(j) < target){
                    count++;
                }
            }
        }

        return count;
    }
}

📌 Tip

num.size()를 반복해서 호출하지 말고, 미리 int n = num.size()로 할당해놓으면 성능이 더 좋아짐.

Two Pointers Algorithem

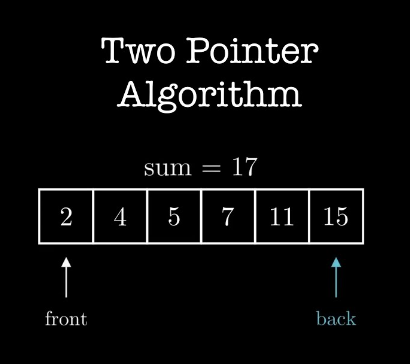
투 포인터 알고리즘(Two Pointers Algorithem)
- 1차원 배열에서 각자 다른 원소를 가리키고 있는 2개의 포인터를 조작해가면서 원하는 값을 찾을 때 까지 탐색하는 알고리즘
- 리스트에 순차적으로 접근해야 할 때 두 개의 점(포인터)의 위치를 기록하면서 처리한다.

동작 방식 & 구현

보통 left(l), riget(r)이나 start(s), end(d)와 같은 식으로 포인트의 이름을 붙임
- 포인트 2개: start, end
- 찾는값: target
처음에는 start=end=0이고, 조건은 항상 두 포인터들의 관계는 start<=end인 것이다.
2개의 포인터는 현재 부분 배열의 시작(start)과 끝(end)을 가리킨다.

Two-Pointer 시간 복잡도

매 루프마다 항상 두 포인터 중 하나는 1씩 증가한다. 각 포인터를 start, end라고 했을 때 start와 end는 최대 N까지 증가할 수 있고, 항상 start<=end이다. 둘이 증가하는 과정은 최대 N번만 반복된다. O(N^2)가 걸리는 문제를 O(N)에 해결할 수 있다.

💻 적용 코드

import java.util.Arrays;
import java.util.List;

class Solution {
    public int countPairs(List<Integer> nums, int target) {
        int count = 0;
        // List를 배열로 변환
        Integer[] numsArray = nums.toArray(new Integer[0]);
        // 배열 정렬
        Arrays.sort(numsArray);
        
        int left = 0;
        int right = numsArray.length - 1;
        
        while (left < right) {
            int sum = numsArray[left] + numsArray[right];
            
            // 합이 target보다 작으면, left와 right 사이의 모든 값들이 조건을 만족
            if (sum < target) {
                count += right - left;
                left++; // left 포인터를 오른쪽으로 이동
            } else {
                right--; // 그렇지 않으면 right 포인터를 왼쪽으로 이동
            }
        }
        
        return count;
    }
}