레이지 프로퍼게이션 (Lazy Propagation)

세그먼트 트리는 무궁무진한 활용이 가능한 자료구조입니다. 레이지 프로퍼게이션은 그 활용 중 하나로 레이지 세그와 함께라면 백준의 많은 문제들을 해결할 수 있습니다.

대부분 알고리즘의 기본적인 최적화 원리는 다음과 같습니다.

• 반복되는 연산을 줄이고, 겹치는 건 한 번만 계산해서 활용하자.

수열의 구간 합을 구하는 문제는 누적 합(Prefix Sum)으로 해결했습니다.
업데이트되는 수열의 구간 합을 구하는 문제는 세그먼트 트리(Segment Tree)로 해결했습니다.

그리고, 구간 업데이트되는 수열의 구간 합을 구하는 문제를 레이지 프로퍼게이션(Lazy Propagation)으로 해결할 수 있습니다.

시간 복잡도

세그먼트 트리에서 어떤 한 점을 업데이트하는 데는 $O(logN)$이 들어갑니다.

따라서 구간을 업데이트하는 데 $O(NlogN)$이 필요합니다.
그런데 일반적인 배열에서 구간 업데이트를 실행하면 $O(N)$입니다.
기존의 세그먼트 트리로 구간 업데이트를 수행하면 일반적인 배열을 쓰는 것보다 못합니다.

구간을 업데이트하는 과정을 머리에 그려보면, 상당히 많은 노드가 여러 번 참조되는 걸 확인할 수 있습니다.
이 부분을 줄이면 최적화가 가능합니다.

실제로, 구간 업데이트도 $O(logN)$에 실행할 수 있습니다.
이 방법이 레이지 프로퍼게이션(Lazy Propagation)입니다.

실행 과정

레이지 프로퍼게이션(Lazy Propagation)의 기본 원리는 단어 그대로 업데이트를 미루는 것입니다.

아래 이야기를 읽어봅시다.

친구 20명과 같이 학교에 가려고 합니다.
학교와는 거리가 멀어 버스를 타야만 하는데, 이 친구들은 1분 간격으로 정류장에 도착합니다.
먼저 도착한 친구가 매정하게 버스를 먼저 타고 떠나면 버스는 20대가 필요하겠죠?
하지만 기다렸다가 친구들이 모두 도착한 후에 버스를 타면 버스 1대로 모두 학교에 갈 수 있습니다.

이러한 원리로 레이지 프로퍼게이션(Lazy Propagation)이 작동합니다.
정말 필요할 때만 업데이트를 해주고, 필요 없을 때는 우리가 과제를 미루듯 쌓아놓는 것이죠.

아래 트리를 봅시다.

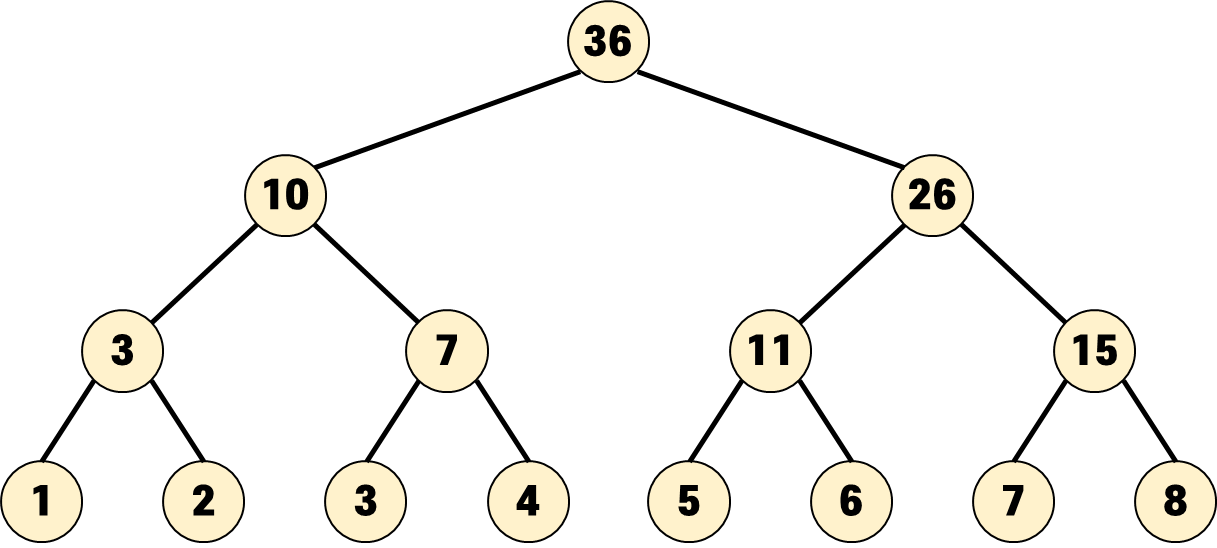
평범해 보이는 세그먼트 트리입니다.
tree[node] = tree[node*2] + tree[node*2+1] 형태로 구성되어 있는 익숙한 구간 합 트리입니다.

여기서 업데이트를 미뤄둘 lazy 요소를 넣어봅시다.

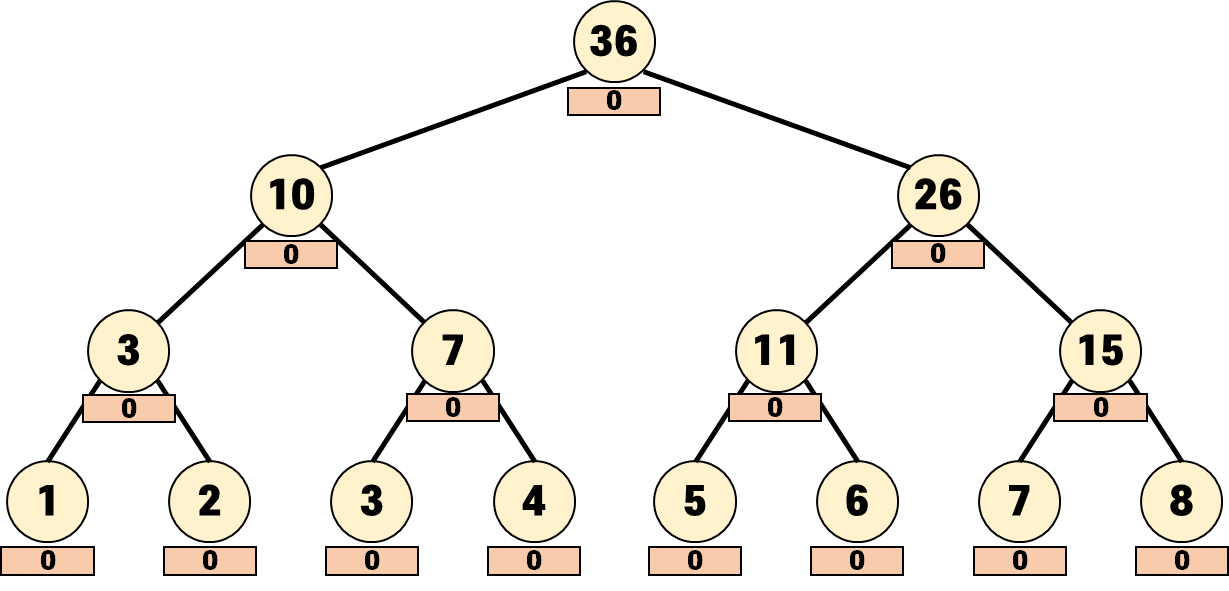
각 노드 밑에 달려있는 명찰이 그 노드가 미뤄놓은 lazy입니다.
방금 생성되었기 때문에 lazy는 모두 0입니다.

이제 업데이트를 해보면서 레이지 프로퍼게이션(Lazy Propagation)에 대한 감을 잡아봅시다.

구간 [1, 6]에 3을 더하는 과정을 봅시다.

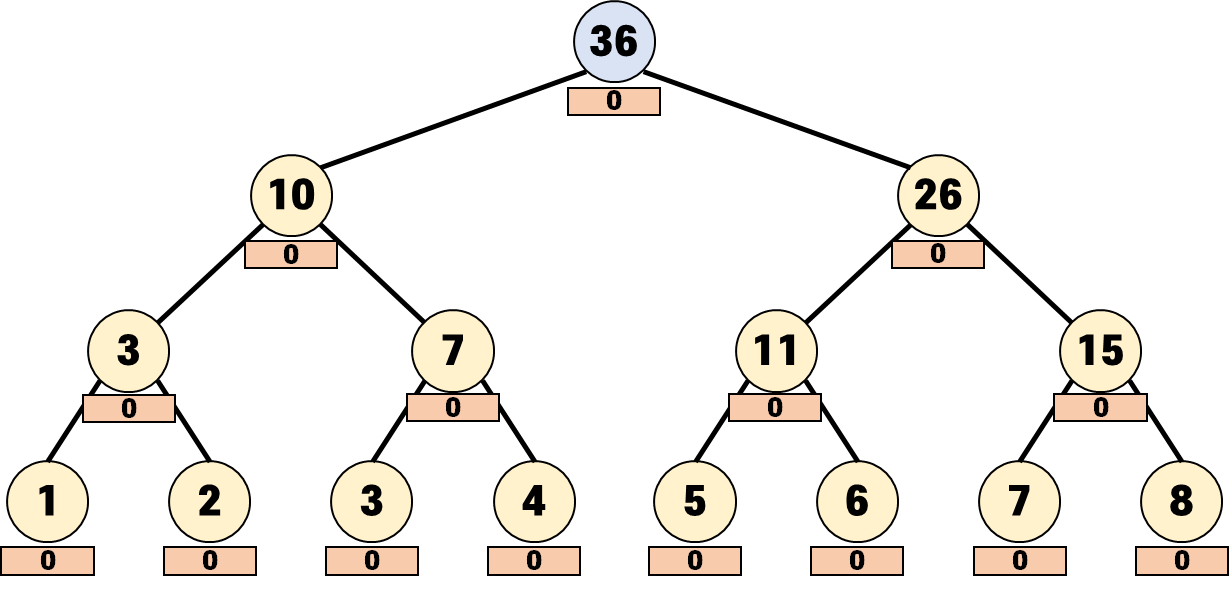
루트 노드를 살펴봅니다.
루트 노드는 업데이트 대상 노드가 아니므로 자식노드들로 내려갑니다.

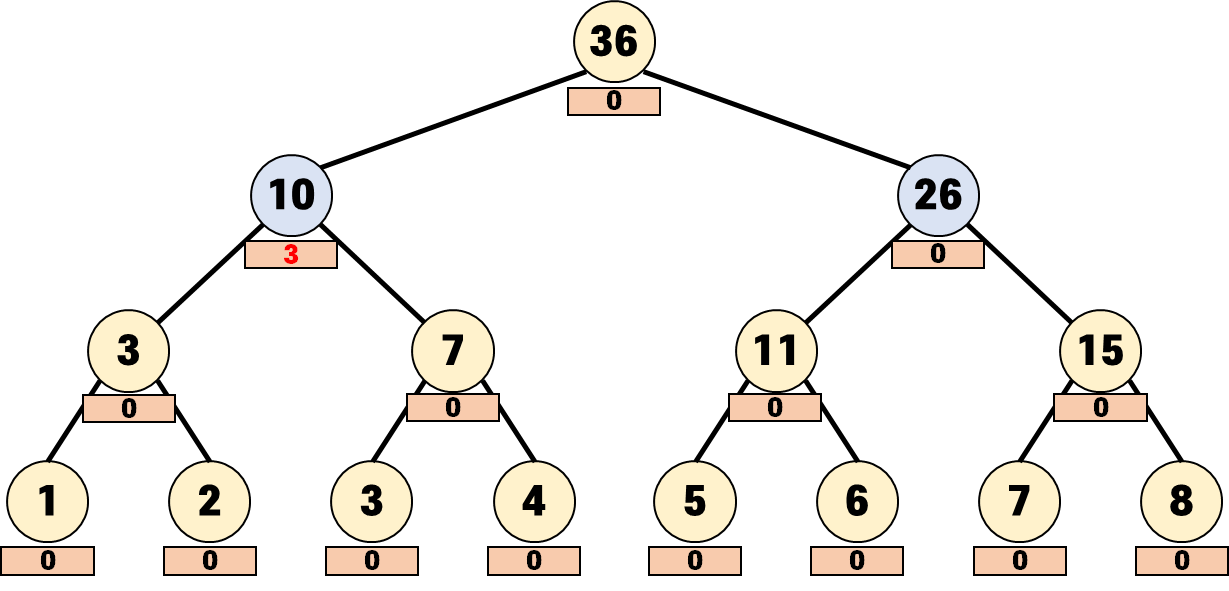
왼쪽 자식 노드는 [1, 4]를 담당하므로 해당 서브트리는 모두 업데이트가 되어야 합니다.
이렇게 노드가 담당하는 구간이 업데이트하고자 하는 구간에 속할 때 더 내려가지 않고 lazy에 미뤄둡니다.

오른쪽 자식 노드는 [5, 8]이므로 한번 더 내려갑니다.

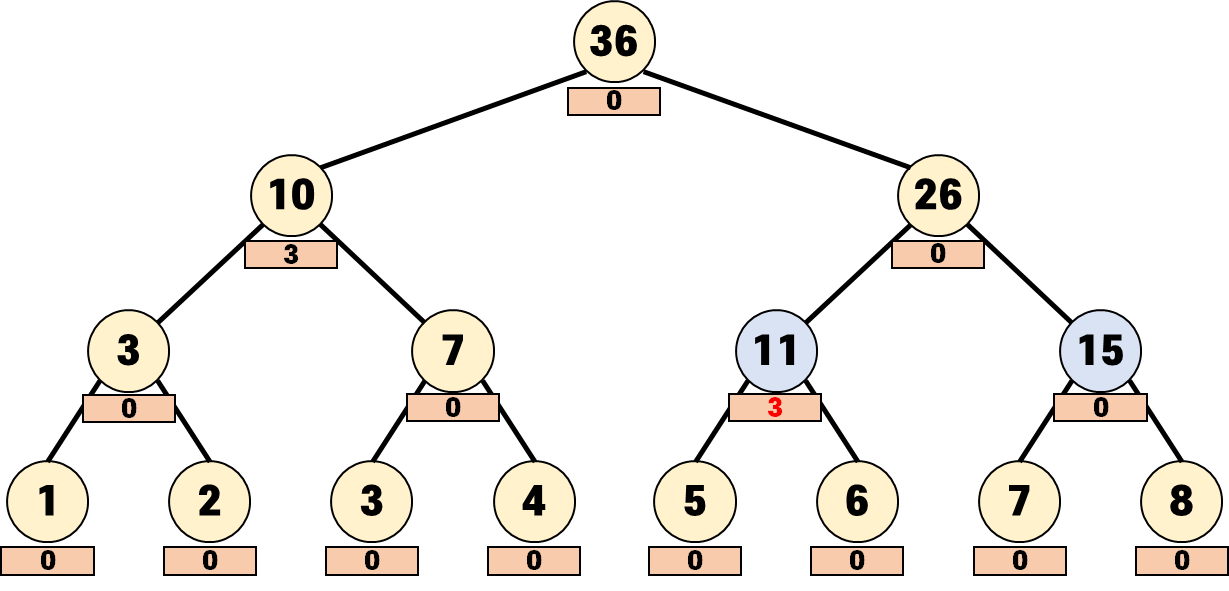
[5, 6]을 담당하는 노드는 역시 [1, 6]에 속하므로 lazy를 업데이트해줍니다.

[7, 8] 노드는 구간에 걸쳐있지 않으므로 중단합니다.

아래는 최종 완료된 트리입니다.

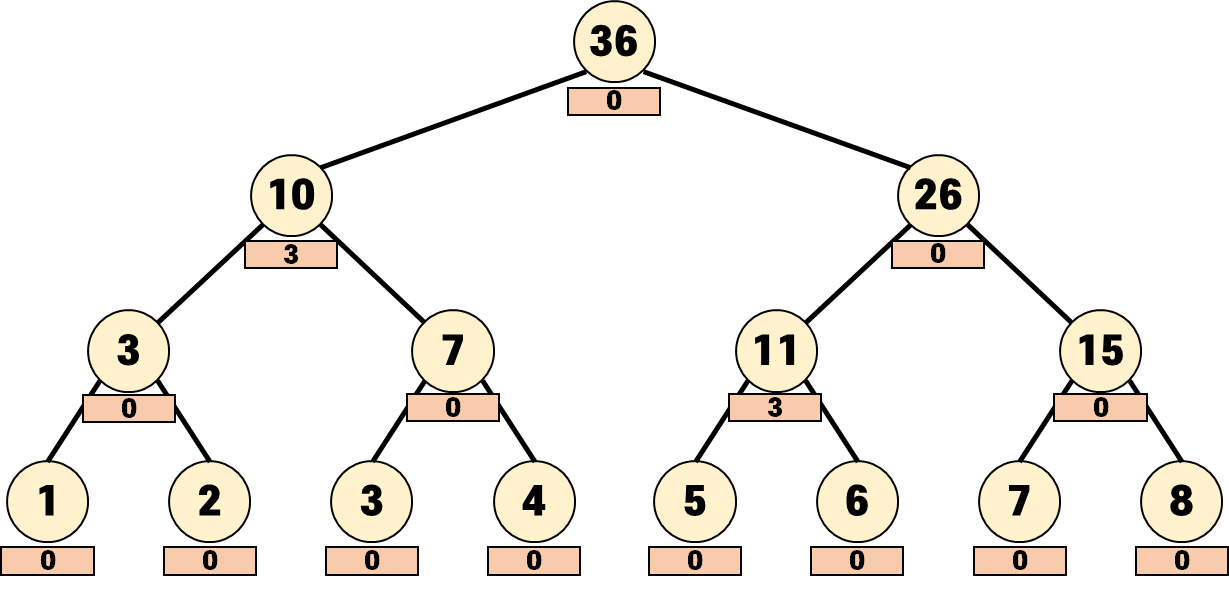
미뤄둔 업데이트 실행

이제 언제 lazy를 트리에 업데이트해야 하는지 살펴보도록 합시다.

우리에게 주어진 과제는 미루지 말고 일찍 끝내버리는 것이 현명합니다.
그러나 세그먼트 트리는 최대한 미루면 미룰수록 더욱 이득입니다.

과제를 극한까지 미루는 우리들이라면 알 수 있습니다. 최대한 미루고 미루다가 어쩔 수 없이 해야 할 때, 그 때 세그트리는 업데이트됩니다.
바로 그 노드를 참조할 때 업데이트하면 됩니다.

숙제를 검사하는 기간이 오면 그제서야 숙제를 하는 것처럼 레이지 프로퍼게이션(Lazy Propagation)도 그렇게 작동시키면 됩니다.

구간 [3, 3]의 값을 확인해봅시다.

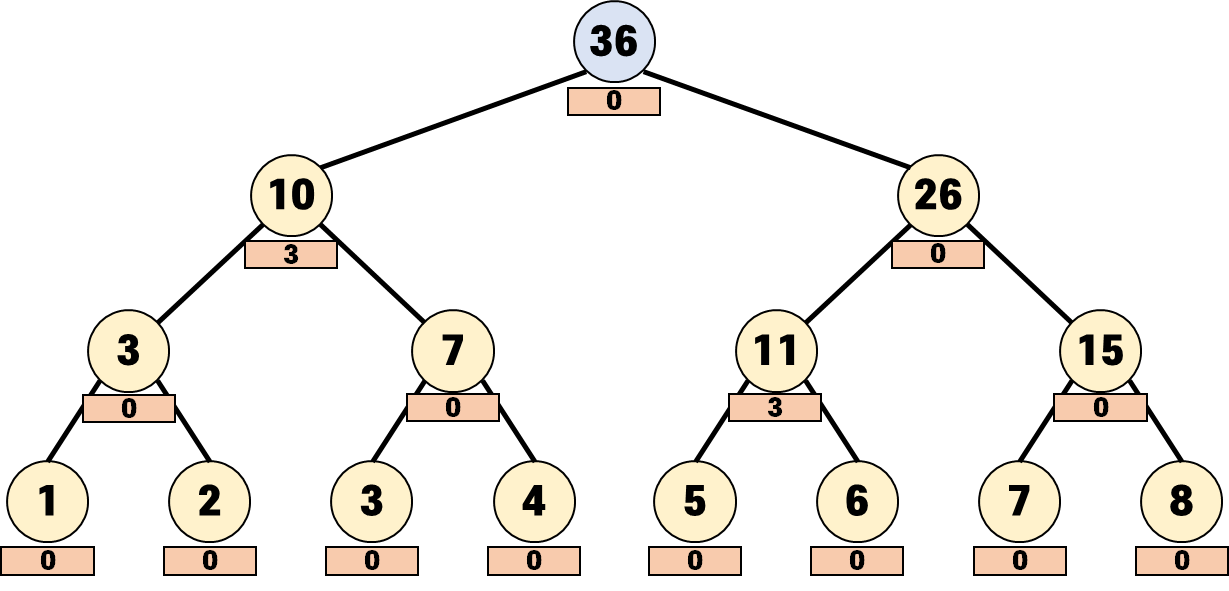
루트 노드를 검사합니다. 루트 노드의 lazy 값은 0이므로 아무런 변화가 일어나지 않습니다.
이제 자식 노드로 내려갑시다.

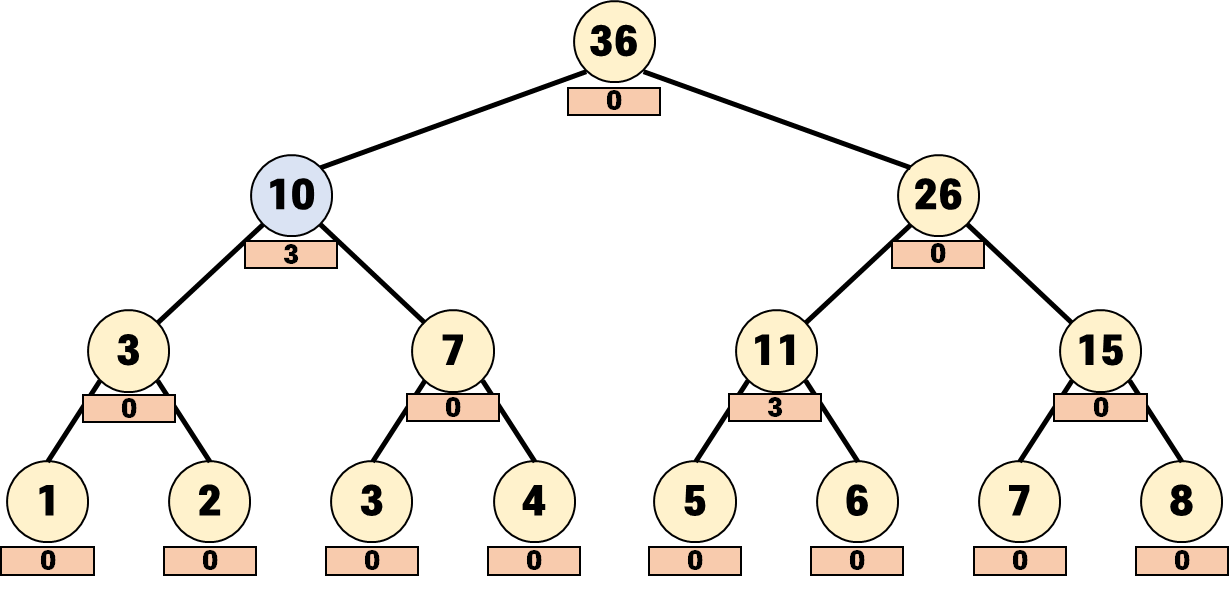
오른쪽 자식은 범위 외니까 중단되고, 왼쪽 자식은 lazy 값이 있습니다.
이제 이 값을 업데이트해줘야 합니다.

노드가 [s, e] 구간을 담당하고 있을 때, 구간 합 트리에서는 tree[node] += (e-s+1) * lazy 가 됩니다.
모든 구간에 lazy 값을 더해야 하므로 해당 노드는 (구간의 개수) $\times$ lazy값 만큼 더해집니다.

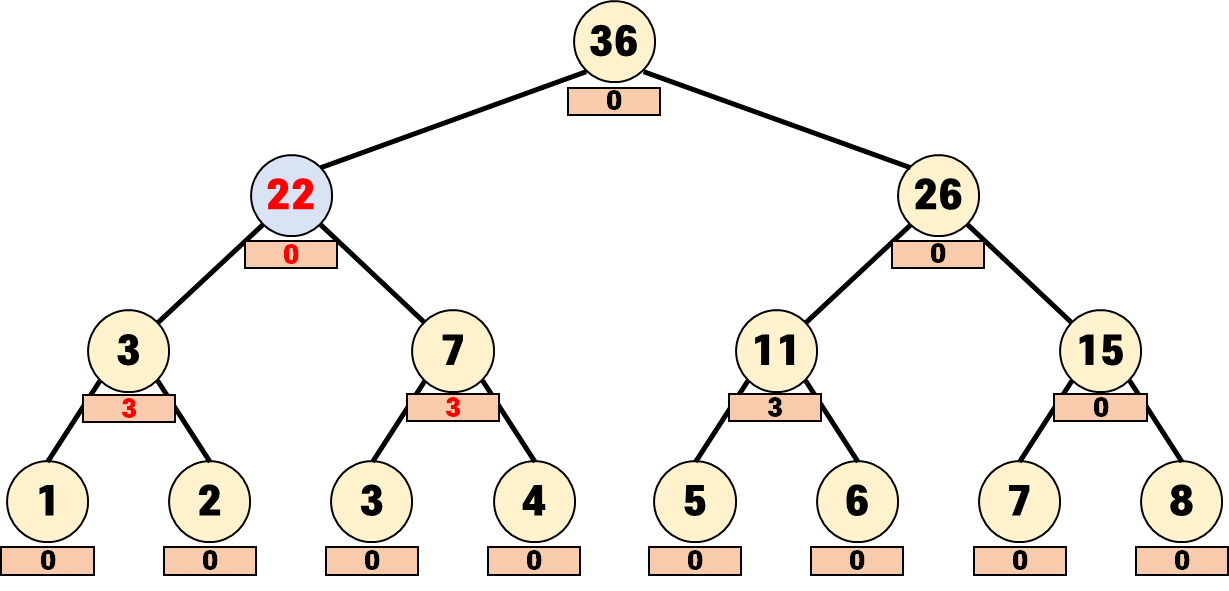
업데이트를 한 후 lazy 값은 0이 되고, 자식에게 전파됩니다.
여기까지가 lazy가 있는 노드에서 일어나는 업데이트 과정입니다.
이후에는 같은 과정을 자식 노드에서 수행합니다.

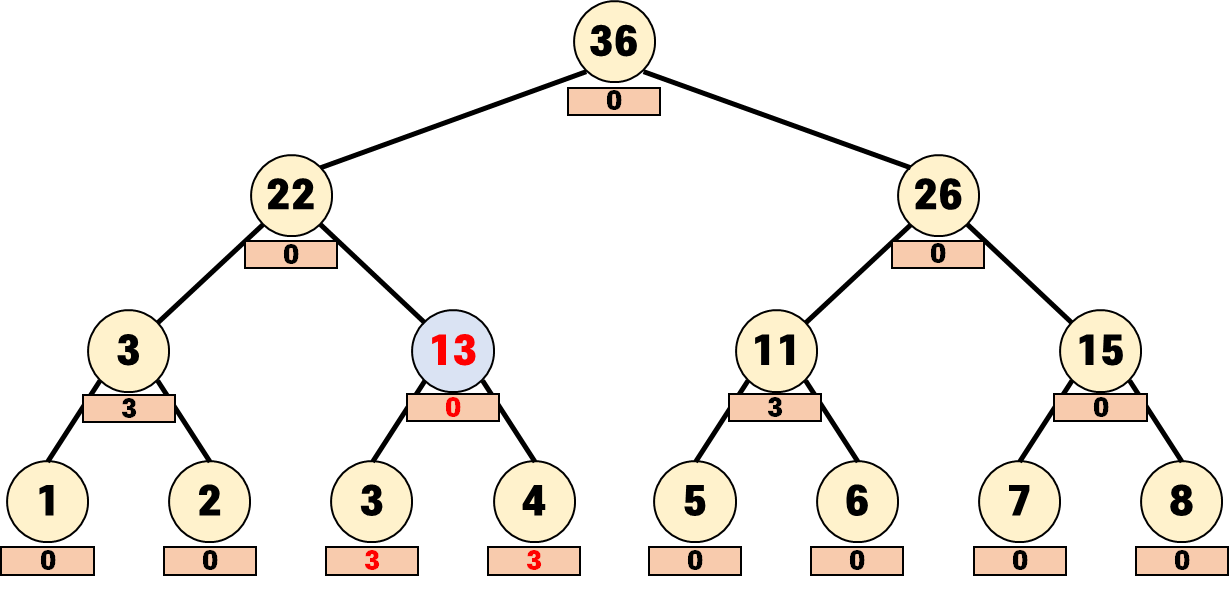
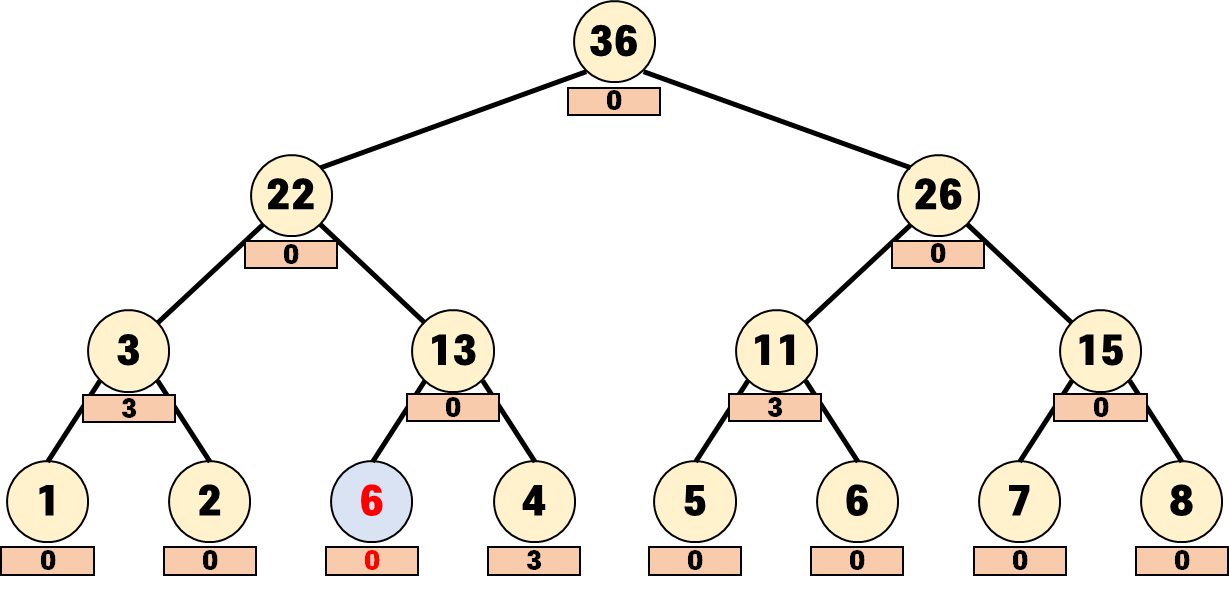
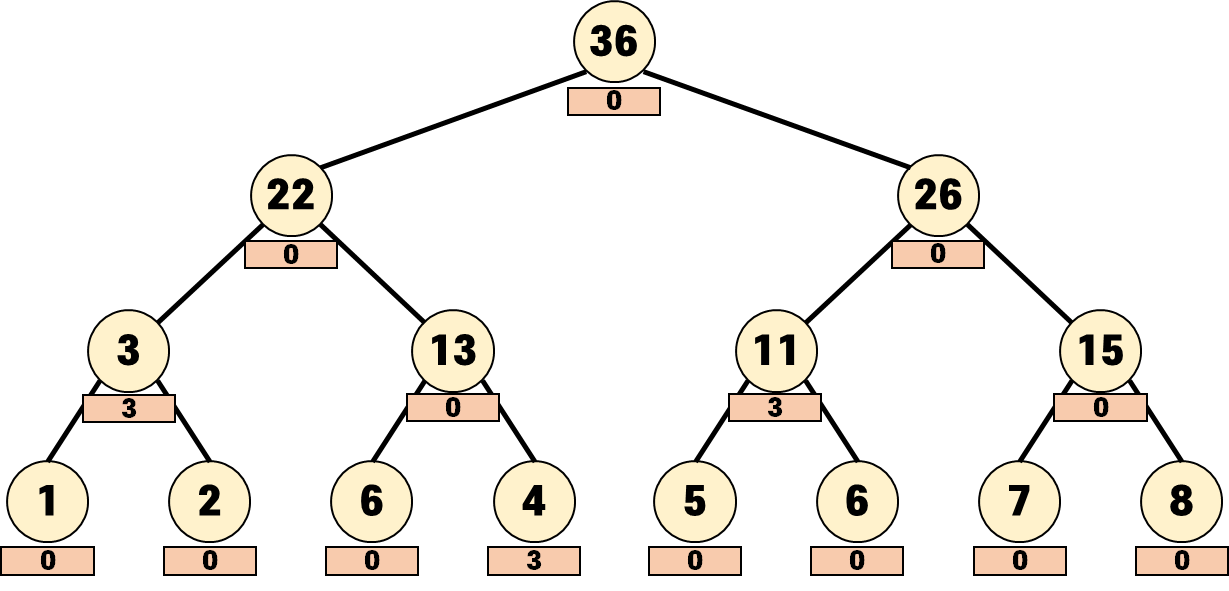
이렇게 [3, 3]의 값으로 7이 반환됩니다.
여기서 눈치챘겠지만 lazy값이 모두 전파된 후에야 그 노드의 진짜 값이 드러납니다.

[4, 4] 노드는 현재 4가 저장되어 있지만 실제로는 lazy가 전파된 후인 7이 진짜 값인 것처럼 lazy가 전파되어야 진짜 값을 찾을 수 있습니다.

따라서 update(), query()같은 모든 과정은 해당 노드의 lazy를 전파한 후에 이루어져야 합니다.

위 과정을 C++로 구현한 세그트리 클래스는 아래에 있습니다.

코드

class SegTree{
private:
	vector<int> tree;
	vector<int> lazy;
public:
	SegTree(int N){
		tree.resize(N*4);
		lazy.resize(N*4);
	}
	
	int init(vector<int> &nums, int node, int s, int e){
		if (s == e) return tree[node] = nums[s];
		
		return tree[node] = init(nums, node*2, s, (s+e)/2) + init(nums, node*2+1, (s+e)/2+1, e);
	}
	
	void update_range(int node, int s, int e, int l, int r, int dx){
		push(node, s, e);
		if (e < l || r < s) return; // break condition
		if (s >= l && e <= r){ // tag condition
			lazy[node] += dx;
			push(node, s, e);
			return;
		}
		
		update_range(node*2, s, (s+e)/2, l, r, dx);
		update_range(node*2+1, (s+e)/2+1, e, l, r, dx);
		tree[node] = tree[node*2] + tree[node*2+1];
	}
	
	void push(int node, int s, int e){
		if (lazy[node] != 0){
			tree[node] += (e-s+1)*lazy[node];
			if (s != e){
				lazy[node*2] += lazy[node];
				lazy[node*2+1] += lazy[node];
			}
			lazy[node] = 0;
		}
	}
	
	int query(int node, int s, int e, int l, int r){
		push(node, s, e);
		if (s > r || l > e) return 0;
		if (l <= s && e <= r) return tree[node];
		
		return query(node*2,s,(s+e)/2,l,r) + query(node*2+1, (s+e)/2+1,e,l,r);
	}
	
};