BOJ 8462 | 배열의 힘

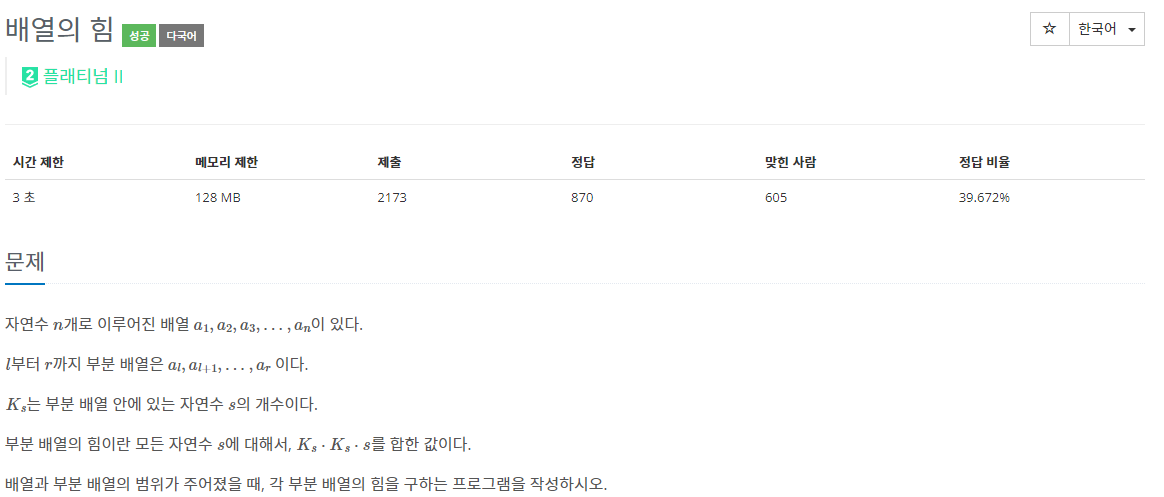
[l, r] 범위 내의 부분 배열에서의 모든 자연수 s에 대해 K_s를 그 부분 배열 내의 s의 개수라고 하고, 모든 s의 (K_s)^2 * s 를 구하는 문제다.

(n+1)^2 - n^2 = 2n+1 이라는 간단한 원리로 해결했다.

역시나 mo's 알고리즘 연습 문제다.

#include <bits/stdc++.h>
using namespace std;

#ifdef LOCAL
constexpr bool local = true;
#else
constexpr bool local = false;
#endif

#define FASTIO ios_base::sync_with_stdio;cin.tie(nullptr);

#define debug if constexpr (local) std::cout
#define endl '\n'
#define lint long long

struct Query{
	int l, r;
	int idx;
};

int n, m;
vector<int> arr;
vector<Query> q;
lint ans[1000001];
lint cnt[1000001];

const int BUCKET_SIZE = 320;

bool _cmp(Query a, Query b){
	int al = a.l / BUCKET_SIZE;
	int bl = b.l / BUCKET_SIZE;
	
	if (al != bl) return al < bl;
	return a.r < b.r;
}

void _Add(int x, lint &sum){
	sum += (cnt[x] * 2 + 1) * x;
	cnt[x]++;
}

void _Minus(int x, lint &sum){
	sum -= (cnt[x]*2 - 1) * x;
	cnt[x]--;
}

int main(){
	FASTIO;
	arr.resize(100001);
	
	cin >> n >> m;
	for (int i = 1; i <= n; i++){
		int t; cin >> t;
		arr[i] = t;
	}
	for (int i = 0; i < m; i++){
		int l, r; cin >> l >> r;
		q.push_back({l, r, i});
	}
	
	sort(q.begin(), q.end(), _cmp);
	
	int lp = 0, rp = 0;
	lint sum = 0;
	
	for (int i = 0; i < m; i++){
		int l = q[i].l, r = q[i].r;
		int idx = q[i].idx;
		
		
		while (l < lp){
			_Add(arr[--lp], sum);
		}
		while (l > lp){
			_Minus(arr[lp++], sum);
		}
		while (rp < r){
			_Add(arr[++rp], sum);
		}
		while (rp > r){
			_Minus(arr[rp--], sum);
		}
		
		debug << "DEBUG sum :: " << sum << endl;
		
		ans[idx] = sum;
	}
	
	for (int i = 0; i < m; i++){
        cout << ans[i] << endl;
    }
	
}