이번 파트에선 시스템 모델이 비선형인 경우에 적용 가능한 비선형 칼만 필터에 대해 알아보자!
대부분의 실제 시스템은 비선형 모델로 표현되는데, 칼만 필터는 선형 모델 대상!
➡ 비선형 모델을 선형으로 근사해서 선형 칼만 필터 알고리즘을 적용하는 확장 칼만 필터(Ch12), 비선형 시스템 모델을 나타내는 입자들(points, particles)을 활용하는 무향 칼만 필터(Ch13)와 파티클 필터(Ch14)에 대해 알아보자!
우리 주변에 존재하는 시스템 대부분이 비선형이기 때문에, 칼만 필터를 비선형 문제에 적용하려는 연구가 아직까지 활발!
초기 연구자들이 칼만 필터를 비선형 시스템까지 확장한 알고리즘 ➡ 확장 칼만 필터(EKF; Extended Kalman Filter)
비선형 시스템에 칼만 필터를 적용해야 한다면, 오랜 세월 검증되고 자료가 많은 EKF 고려해보기.
❗ 하지만 알고리즘이 발산할 위험이 있다는 큰 단점이 있다는 것도 고려하기. ⬅ EKF 이후에 개발된 알고리즘이 극복하고자 하는 지점
1. 선형화 칼만 필터 (Linearized KF)
: 비선형 모델을 선형화한 다음, 이 선형 모델에 대해 설계한 칼만 필터
선형 칼만 필터 알고리즘과 완전히 동일하지만, 시스템 모델에서 차이가 존재
- 선형 칼만 필터의 시스템 모델은 원래부터 선형
- LKF는 비선형 시스템을 하나의 기준점 주위에서 선형화시켜 얻은 선형 모델 A와 H 사용
두 칼만 필터의 설계 과정은 똑같다.
📍 LKF를 실제 시스템에 적용할 때는 시스템의 운용 범위에 유의하기!!
선형화 모델은 기준점 근처에서만 실제 시스템과 비슷한 특성을 보이기 때문
➡ 실제 시스템에 적용할 땐 선형화 모델이 유효한 범위 내에서만 사용되어야 한다.
📌 선형화 칼만 필터가 성공하려면 비선형 시스템의 선형화 모델이 좋아야 한다.
2. EKF 알고리즘
비선형 시스템 모델
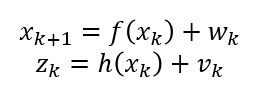
EKF 알고리즘
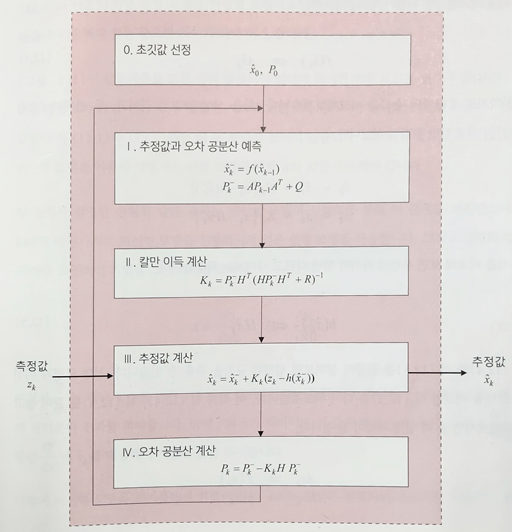
위의 알고리즘을 보면 시스템 행렬 A와 H가 미리 결정되어 있어야 하지만 아직 모르는 변수이다.
➡ 시스템 모델에서 받아와야 한다. 하지만 위에서 본 비선형 시스템 모델 식에선 A와 H가 보이지 않는다.
➡ 비선형 모델의 선형화
비선형 모델을 편미분해서 선형 행렬을 구하는 방법을 써보자! (선형화의 대표적인 기법)

EKF-LKF
- 공통점: 선형화 과정
- 차이점: EKF는
직전 추정값(^x_k)을 선형화 기준으로 삼음
📌 EKF와 LKF 중 어떤 걸 사용할지 판단하는 기준
EKF는 미리 결정된 선형화 기준을 사용하지 않고, 직전 추정값을 기준으로 삼아 매번 새로운 선형화 모델을 구한다.- 시스템의 실제 상태와 가장 가까운 값을 직전 추정값으로 보고, 이 값을 기준으로 선형 모델을 계산
➡ 선형화의 기준점을 사전에 설정하기 어려운 시스템에 적합
➡ 선형화의 기준을 이미 알고 있다면LKF사용!
- 시스템의 실제 상태와 가장 가까운 값을 직전 추정값으로 보고, 이 값을 기준으로 선형 모델을 계산
(선형화의 기준을 미리 알 수 있는 경우는 일정 궤도를 도는 위성, 궤적이 미리 정해져 있는 위성 발사체 등)
EKF 알고리즘의 전체 과정은 선형 칼만 필터 알고리즘과 같다.
각 단계별 계산식에서 차이점 2가지!
- 선형 모델식
Ax_k, Hx_k대신 비선형 시스템 모델식f(x_k), h(x_k) - 비선형 모델의
야코비안으로 행렬 A, H 구함- 이때 야코비안 행렬은 직전 추정값으로 계산
두 예제를 살펴보자!
- 레이다로 물체까지의 거리를 측정해서 이동 속도와 고도를 추정해내는 문제
- 측정 모델이 비선형인 시스템 EKF를 설계하는 방법 소개
- 앞 장에서 소개한 자이로와 가속도계를 융합해서 기울기 자세를 추정해내는 문제
- 측정 모델은 선형, 시스템 모델은 비선형인 시스템
3. 예제1: 레이다 추적
물체까지의 직선 거리를 측정해서 위치와 고도를 추정해보자!
📌 목표: 측정 모델이 비선형인 시스템에 대해 EKF 설계하는 것
문제를 단순하게 하기 위해 물체는 2차원 평면 상에서 일정한 고도와 속도를 유지하면서 움직인다고 가정하자. (고도와 물체의 이동 속도는 모르는 값)
시스템 모델

식 (12.7)과 (12.8)의 시스템 모델을 모두 구했다.
(12.7)은 선형인데, (12.8)의 측정 모델은 비선형!
➡ 선형 칼만 필터를 바로 적용하진 ❌
EKF 함수
식 (12.7)의 시스템 모델은 선형
➡ EKF 알고리즘에서 상태 변수를 예측할 때 선형 칼만 필터 수식 사용

EKF 알고리즘은 아래 식과 같은 이산 시스템에 관한 알고리즘. 하지만 식 (12.7)의 시스템 모델은 이산 시스템이 아니다.
➡ 시스템 모델을 이산 시스템으로 변경해야 함
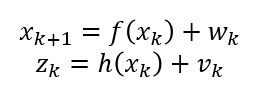
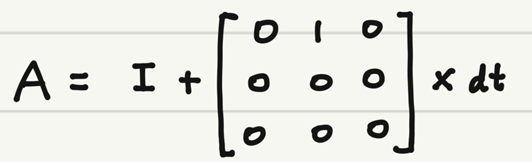
식 (12.7)을 이산화하면 시스템 행렬 A는 아래와 같다.
아래의 이산 시스템 모델은 식 (12.7)을 오일러 적분법으로 dt시간 동안 적분한 결과
측정 모델은 비선형 모델
➡ 행렬 H는 아래와 같이 식 (12.8)의 야코비안을 계산해야 한다.
식 (12.10)
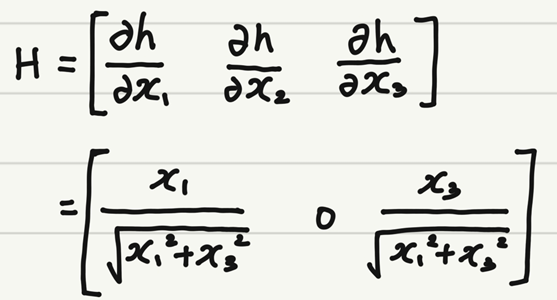
RadarEKF(z,dt)
- 매개변수: z(측정 거리), dt(샘플링 간격)
- 반환값: 수평 위치, 이동 속도, 고도
: EKF 알고리즘 구현. EKF 알고리즘 순서에 따라 추정값 계산.
-
EKF 알고리즘을 시작하기 전에 H 먼저 계산
- Hjacob함수는 식 (12.10)에 따라 측정 모델의 야코비안 H를 계산하는 서브 함수
- 상태 변수를 인자로 받아 H 반환
- Hjacob함수는 식 (12.10)에 따라 측정 모델의 야코비안 H를 계산하는 서브 함수
-
EKF는 선형 모델을 구할 때 현재의 추정값을 기준으로 선형 모델을 구하므로, 이 함수도 현재의 추정값을 인자로 받아야 한다.
- 최초로 실행할 때는 상태 변수의 초기 추정값(^x_0)으로 선형 모델을 구한다. ➡ 최대한 정확한 초깃값을 찾아야 함!!
- 임의로 예측한 초기 추정값이 실제 상태와 많이 다르면 알고리즘이 발산하는 문제 발생!
(시스템 모델의 오차 커짐 ➡ EKF 추정값 오차 커짐 ➡ 이 추정값으로 계산한 시스템 모델 오차 커짐)
- 임의로 예측한 초기 추정값이 실제 상태와 많이 다르면 알고리즘이 발산하는 문제 발생!
- 최초로 실행할 때는 상태 변수의 초기 추정값(^x_0)으로 선형 모델을 구한다. ➡ 최대한 정확한 초깃값을 찾아야 함!!
-
hx 함수는 식 (12.8)의 측정 모델식을 구현한 함수
<function [pos, vel, alt] = RadarEKF(z, dt)
%
%
persistent A Q R
persistent x P
persistent firstRun
if isempty(firstRun)
A = eye(3) + dt*[ 0 1 0;
0 0 0;
0 0 0 ];
Q = [ 0 0 0;
0 0.001 0;
0 0 0.001 ];
R = 10;
x = [0 90 1100]'; % 임의로 예측한 초기 추정값
P = 10*eye(3);
firstRun = 1;
end
H = Hjacob(x); % 시스템 행렬의 야코비안 H 계산
xp = A*x;
Pp = A*P*A' + Q;
K = Pp*H'*inv(H*Pp*H' + R);
x = xp + K*(z - hx(xp));
P = Pp - K*H*Pp;
pos = x(1);
vel = x(2);
alt = x(3);
%---------------------------------
function zp = hx(xhat) % 직선 거리 반환
%
%
x1 = xhat(1);
x3 = xhat(3);
zp = sqrt(x1^2 + x3^2);
%---------------------------------
function H = Hjacob(xp)
%
%
H = zeros(1, 3);
x1 = xp(1);
x3 = xp(3);
H(1) = x1 / sqrt(x1^2 + x3^2);
H(2) = 0;
H(3) = x3 / sqrt(x1^2 + x3^2);
GetRadar.m
: 레이다의 직선 거리를 측정하는 함수
이렇게 가상으로 측정 잡을 만드는 코드는 실제 시스템에선 필요❌
일정한 고도에서 정속으로 이동하는 물체의 동역학 방정식이 구현되어 있다.
- 고도 1km에서 100m/s의 속도로 움직인다고 가정
- 고도, 속도는 평균값. 실제로는 잡음이 있으니까 잡음 반영.
- 레이다가 측정하는 직선 거리도 측정 오차가 있다고 가정. 오차 범위는 측정 거리의 5% 내외
function r = GetRadar(dt)
%
%
persistent posp
if isempty(posp)
posp = 0;
end
vel = 100 + 5*randn;
alt = 1000 + 10*randn;
pos = posp + vel*dt;
v = 0 + pos*0.05*randn;
r = sqrt(pos^2 + alt^2) + v;
posp = pos;TestRadarEKF.m
- 레이다로 측정한 직선 거리 값을 EKF 함수에 넘겨 위치, 속도, 고도의 추정값을 받아오고 그래프로 그린다.
clear all
dt = 0.05;
t = 0:dt:20;
Nsamples = length(t);
Xsaved = zeros(Nsamples, 3);
Zsaved = zeros(Nsamples, 1);
for k=1:Nsamples
r = GetRadar(dt);
[pos, vel, alt] = RadarEKF(r, dt);
Xsaved(k, :) = [pos vel alt];
Zsaved(k) = r;
end
PosSaved = Xsaved(:, 1);
VelSaved = Xsaved(:, 2);
AltSaved = Xsaved(:, 3);
t = 0:dt:Nsamples*dt-dt;
figure
plot(t, PosSaved)
figure
plot(t, VelSaved)
figure
plot(t, AltSaved)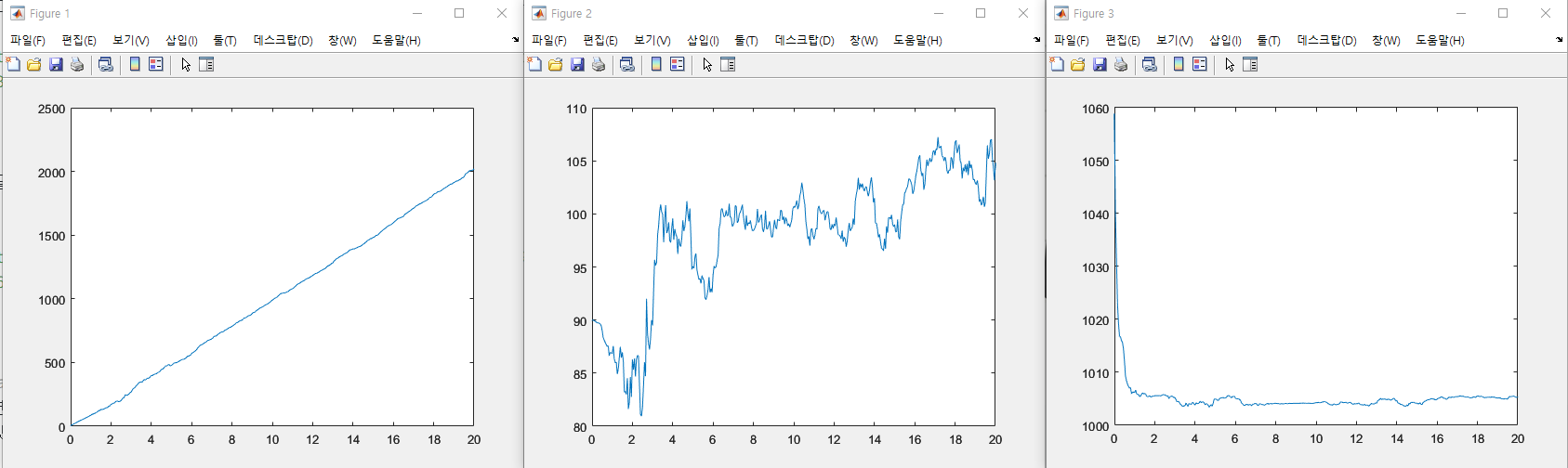
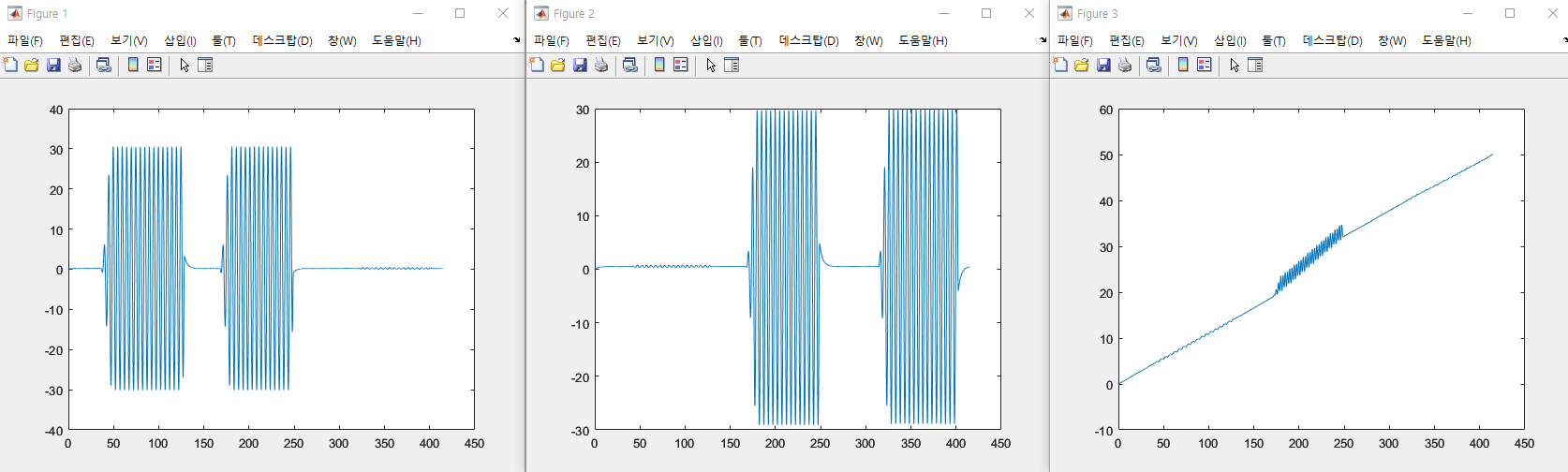
Figure 2
: 속도 추정값
- 추정값의 궤적을 보면 실제 속도의 평균 100m/s로 잘 추정
- 초깃값 오차 때문에 초기 추정 오차가 크지만, 시간이 지나면서 속도 추정값이 명목 속도 근방으로 수렴
- 여기선 초깃값 영향을 보기 위해 일부러 오차를 준 것
- 오차를 10% 줬지만, 발산하지 않고 잘 작동함
- EKF에선 초깃값을 최대한 정확하게 선정하기!
- 여기선 초깃값 영향을 보기 위해 일부러 오차를 준 것
Figure 1
: 고도 추정값
- 추정값의 궤적을 보면 실제 고도의 평균 1000m로 잘 추정
- 속도와 마찬가지로 초기 예측값에 10% 오차(1100m)를 줬지만 발산하지 않고 수렴
Figure 3
: 수평 거리 추정값
- 평균 100m/s 속도로 20초 동안 이동하면 2000m 이동하는데, 추정 거리도 비슷
📌 레이다가 측정한 직선 거리 & EKF로 추정한 고도와 수평 거리로 계산한 추정 거리를 비교해보면 측정값의 잡음이 거의 제거되었고, 물체의 이동에 따른 측정 거리 변화도 잘 반영되었음을 확인 가능
4. 예제2: 기울기 자세 측정
시스템 모델이 비선형인 문제를 보자!
상태 변수를 오일러 각도에서 쿼터니언으로 변환해야만 했던 11장의 자이로와 가속도계를 이용한 기울기 자세 측정 예제를 다시 다뤄보자!
시스템 모델

EKF 함수
EKF를 구현하기 위해선 식 (12.11)의 야코비안을 알아야 한다.
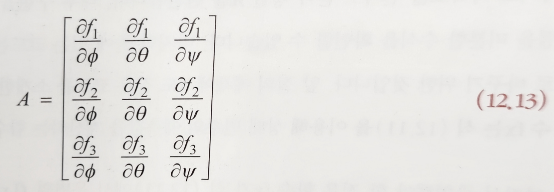
위의 식은 식 (12.11)의 야코비안 정의이다.
이 정의에 식 (12.11)을 대입해서 미분하면 행렬 A의 수식이 나온다.
하지만 식 (12.13)은 이산 시스템의 야코비안이 아니다.
➡ 구현할 땐 이 행렬을 이산 시스템으로 변환해야 한다!
EulerEKF(z, rates, dt)
- 매개변수: z(가속도계의 자세각), rates(자이로 각속도), dt(샘플링 간격)
- 반환값: 추정 오일러각
Ajacob 함수
- 식 (12.13)의 야코비안 계산
- 매개변수: 상태 변수, 자이로 각속도
- 반환: 행렬 A
function [phi, theta, psi] = EulerEKF(z, rates, dt)
%
%
persistent H Q R
persistent x P
persistent firstRun
if isempty(firstRun)
H = [ 1 0 0;
0 1 0 ];
Q = [ 0.0001 0 0;
0 0.0001 0;
0 0 0.1 ];
R = [ 10 0;
0 10 ];
x = [0 0 0]';
P = 10*eye(3);
firstRun = 1;
end
A = Ajacob(x, rates, dt); % 야코비안 계산
xp = fx(x, rates, dt); % 상태변수 예측값 계산 함수 호출
Pp = A*P*A' + Q;
K = Pp*H'*inv(H*Pp*H' + R);
x = xp + K*(z - H*xp);
P = Pp - K*H*Pp;
phi = x(1);
theta = x(2);
psi = x(3);
%------------------------------
function xp = fx(xhat, rates, dt)
%
%
phi = xhat(1);
theta = xhat(2);
p = rates(1);
q = rates(2);
r = rates(3);
xdot = zeros(3, 1);
xdot(1) = p + q*sin(phi)*tan(theta) + r*cos(phi)*tan(theta);
xdot(2) = q*cos(phi) - r*sin(phi);
xdot(3) = q*sin(phi)*sec(theta) + r*cos(phi)*sec(theta);
xp = xhat + xdot*dt;
%------------------------------
function A = Ajacob(xhat, rates, dt)
%
%
A = zeros(3, 3);
phi = xhat(1);
theta = xhat(2);
p = rates(1);
q = rates(2);
r = rates(3);
A(1,1) = q*cos(phi)*tan(theta) - r*sin(phi)*tan(theta);
A(1,2) = q*sin(phi)*sec(theta)^2 + r*cos(phi)*sec(theta)^2;
A(1,3) = 0;
A(2,1) = -q*sin(phi) - r*cos(phi);
A(2,2) = 0;
A(2,3) = 0;
A(3,1) = q*cos(phi)*sec(theta) - r*sin(phi)*sec(theta);
A(3,2) = q*sin(phi)*sec(theta)*tan(theta) + r*cos(phi)*sec(theta)*tan(theta);
A(3,3) = 0;
A = eye(3) + A*dt;TestEulerEKF.m
clear all
Nsamples = 41500;
EulerSaved = zeros(Nsamples, 3);
dt = 0.01;
for k = 1:Nsamples
[p, q, r] = GetGyro();
[ax, ay, az] = GetAccel();
[phi_a, theta_a] = EulerAccel(ax, ay, az);
[phi, theta, psi] = EulerEKF([phi_a theta_a]', [p q r], dt);
EulerSaved(k, :) = [ phi theta psi ];
end
PhiSaved = EulerSaved(:, 1) * 180/pi;
ThetaSaved = EulerSaved(:, 2) * 180/pi;
PsiSaved = EulerSaved(:, 3) * 180/pi;
t = 0:dt:Nsamples*dt-dt;
figure
plot(t, PhiSaved)
figure
plot(t, ThetaSaved)
figure
plot(t, PsiSaved)