
칼만 필터로 2차원 평면 위에서 움직이는 물체를 추적하는 방법에 대해 알아보자!
보통 2차원 영상에서 특정 표적을 감시하고자 할 때 사용!
📌 표적의 위치는 영상 처리 알고리즘으로 알아내야 한다!
(칼만 필터는 영상에서 물체의 위치를 찾아내진 못한다.)
칼만 필터는 영상 처리 기법으로 찾아낸 물체의 위치를 입력 받아 정확한 위치를 추정하는 역할
✔ 표적 추적 문제에서도 칼만 필터의 역할은 영상 처리 알고리즘으로 얻은 위치의 오차를 제거하고 이동 속도 등을 추정하는 것!
1. 시스템 모델
평면 상의 표적 추적에 칼만 필터를 적용하기 위해선 앞 장에 나왔던 위치-속도 모델을 2차원으로 확장해야 한다.
➡ 즉 상태 변수를 x축의 위치/속도, y축의 위치/속도로 잡고 시스템 모델을 유도!

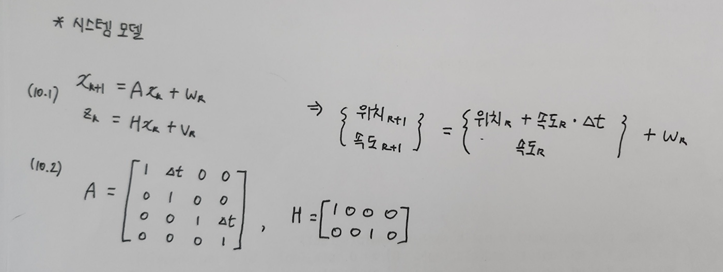
행렬 H를 식 (10.1)의 측정값 관계식에 대입해서 정리해보면, x축과 y축 방향의 위치만 측정하고 속도는 측정하지 않는다는 의미
영상 처리 기술이 다양한 분야에 점점 더 많이 활용되는 추세! ➡ 칼만 필터와 영상 처리 알고리즘을 함께 활용하는 방법을 알아두면 도움이 될 것!
2. 칼만 필터 함수
TrackKalman(xm, ym)
- 매개변수: xm, wm (영상 처리 알고리즘이 찾아낸 위치)
- 반환값: xh, yh (추정 위치)
function [xh, yh] = TrackKalman(xm, ym)
%
%
persistent A H Q R
persistent x P
persistent firstRun
if isempty(firstRun)
dt = 1;
A = [1 dt 0 0
0 1 0 0
0 0 1 dt
0 0 0 1];
H = [1 0 0 0
0 0 1 0];
Q = 1.0*eye(4);
R = [50 0
0 50];
x = [0, 0, 0, 0]';
P = 100*eye(4);
firstRun = 1;
end
xp = A*x;
Pp = A*P*A' + Q;
K = Pp*H'*inv(H*Pp*H' + R);
z = [xm ym];
x = xp + K*(z - H*xp);
P = Pp - K*H*Pp;
% 추정 위치 반환
xh = x(1);
yh = x(3);
end3. 테스트 프로그램 1
농구공이 오른쪽 상단에서 왼쪽 하단까지 대각선 방향으로 이동하는 상황을 생각해보자.
공의 이동 속도는 일정하고, 공의 이동 영상은 1초에 한 번씩 촬영된다.
촬영 영상에서 공의 위치를 찾아내는 알고리즘은 GetBallPos
➡ GetBallPos 함수에서 공의 위치를 측정해서 칼만 필터에 입력하면, 칼만 필터는 추정 위치를 반환!
GetBallPos.m
- 매개변수: 이미지 인덱스
- 반환값: 측정 위치
function [xc, yc] = GetBallPos(index)
%
%
persistent imgBg
persistent firstRun
if isempty(firstRun)
imgBg = imread('Img/bg.jpg');
firstRun = 1;
end
xc = 0;
yc = 0;
imgWork = imread(['Img/', int2str(index), '.jpg']);
imshow(imgWork)
fore = imabsdiff(imgWork, imgBg);
fore = (fore(:,:,1) > 10) | (fore(:,:,2) > 10 | fore(:,:,3) > 10);
L = logical(fore);
stats = regionprops(L, 'area', 'centroid');
area_vector = [stats.Area];
[tmp, idx] = max(area_vector);
centroid = stats(idx(1)).Centroid;
% 공의 중심 좌표 반환
xc = centroid(1) + 15*randn; % 임의로 평균 15픽셀 정도의 잡음 추가 (여기서 사용하는 예제 이미지는 완전히 깨끗한 영상이기 때문)
yc = centroid(2) + 15*randn;
end영상에서 물체를 찾아내는 다양한 알고리즘 중 가장 간단한 배경 이미지(imgBg)와 촬영 이미지(imgWork)의 차이를 이용하는 가장 간단한 알고리즘 사용!
영상 처리 알고리즘에 대해 자세히 알고싶다면 MATLAB Image Processing Toolbox 문서 참고하기
TestTrackKalman.m
clear all
NoOfImg = 24;
Xmsaved = zeros(2, NoOfImg);
Xhsaved = zeros(2, NoOfImg);
for k = 1:NoOfImg
[xm, ym] = GetBallPos(k);
[xh, yh] = TrackKalman(xm, ym);
hold on
plot(xm, ym, 'g*') % GetBallPos 함수가 추정한 위치 표시
plot(xh, yh, 'ys') % 칼만 필터가 추정한 위치 표시
pause(1)
Xmsaved(:, k) = [xm ym]';
Xhsaved(:, k) = [xh yh]';
end
figure
hold on
plot(Xmsaved(1,:), Xmsaved(2,:), '*')
plot(Xhsaved(1,:), Xhsaved(2,:), 's')
set(gca, 'yDir', 'reverse')
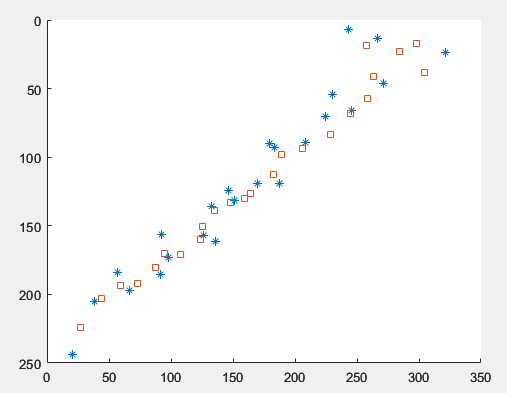
*: GetBallPos 함수의 측정값ㅁ: 칼만 필터의 추정 위치
칼만 필터의 추정 위치가 대각선에 더 가깝게 배치되어 있다.
➡ 칼만 필터가 측정 잡음을 효과적으로 제거해서 더 참값에 가까운 위치를 출력한 것!
오른쪽 상단에 한 점 ㅁ이 대각선에서 크게 벗어나 있는데, 그 이유는 초기 위치 오차 때문.
TrackKalman 함수에서 초기 위치를 (0,0), 즉 초기에 공이 왼쪽 상단에 있다고 가정했다.
테스트 프로그램이 막 시작할 때는 칼만 필터가 충분히 수렴하기 전이라 오차가 크게 나타난 것.
4. 테스트 프로그램 2
행렬 Q와 R을 조율해서 칼만 필터의 성능을 개선해보자!
복습) 7.2절 잡음의 공분산에서 Q와 R은 칼만 필터의 성능에 서로 정반대 영향
- Q가 커지면 칼만 이득이 커짐 ➡ 추정 결과가 측정값에 더 가까워짐
- Q가 작아지면 측정값에 포함된 잡음의 영향이 줄어 추정값이 더 매끄러운 궤적
✔ R은 반대!
TrackKalmanQR.m은 앞의 TrackKalman 함수에서 Q를 0.01*eye(4);로 바꿈
TestTrackKalmanQR.m
clear all
NoOfImg = 24;
Xmsaved = zeros(2, NoOfImg);
Xhsaved = zeros(2, NoOfImg);
Xqrsaved = zeros(2, NoOfImg);
for k = 1:NoOfImg
[xm, ym] = GetBallPos(k);
[xh, yh] = TrackKalman(xm, ym);
[xqr, yqr] = TrackKalmanQR(xm, ym);
hold on
plot(xm, ym, 'r*')
plot(xh, yh, 'bs')
plot(xqr, yqr, 'bo')
pause(1)
Xmsaved(:, k) = [xm ym]';
Xhsaved(:, k) = [xh yh]';
Xqrsaved(:, k) = [xqr, yqr];
end
figure
hold on
%plot(Xmsaved(1,:), Xmsaved(2,:), '*')
plot(Xhsaved(1,:), Xhsaved(2,:), 's')
plot(Xqrsaved(1,:), Xqrsaved(2,:), 'o')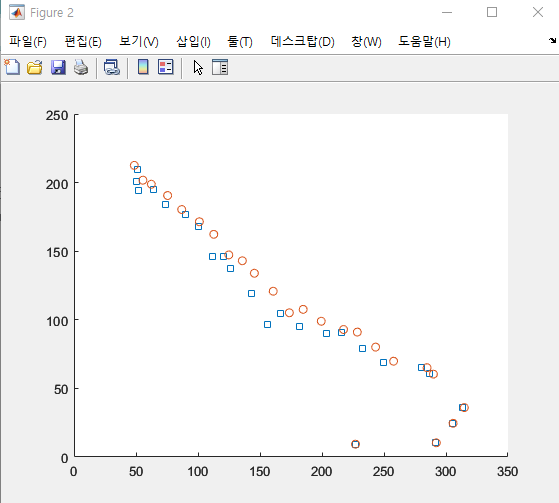
- 원 : 1/100 Q
- 네모: Q
그림을 보면 Q보다 1/100 Q 칼만 필터의 추정값이 잘 움직이지 않는다.
✔ 측정값보다 이전 추정값이 더 많이 반영되기 때문!
✔ 행렬 R의 크기를 키워도 비슷한 경향
