오차역전파 (back propagation)

오차역전파

신경망에서는 gradient descent를 통해 가중치 매개변수 값을 업데이트합니다. 이 때, 가중치 매개변수 값을 오차역전파를 이용하여 계산할 수 있습니다.

다음의 상황을 가정해보겠습니다.

• 문제: 이진 분류
• loss function $L$: cross-entropy (log loss) function
• 훈련 샘플 갯수: 1개 ($\therefore$ loss function = cost function)
• 활성화 함수 $g(x) = \frac{1}{1+e^{-z}}$; sigmoid function
• $\hat{y} = g(wx+b)$

업데이트를 진행할 가중치 매개변수를 $\theta$라 하면, coss function $E(\theta)$는 다음과 같습니다.

• $E(\theta) = L(y - \hat{y}) = -(tln(\hat{y}) + (1-t)ln(1-\hat{y}))$

$\hat{y}$이 $w$와 $b$에 관한 함수 이므로, $E(\theta)$ 역시 $w$와 $b$에 관한 함수입니다. 따라서, $w$와 $b$가 업데이트할 가중치 매개변수입니다.

경사하강법에 의해, 각 layer에서 가중치 매개변수는 다음과 같이 업데이트할 수 있습니다.

• $w_{t+1} := w_t - \epsilon \frac{\partial E(\theta)}{\partial w}$
• $b_{t+1} := b_t - \epsilon \frac{\partial E(\theta)}{\partial b}$, where $\epsilon$: learning rate, $t$: learning step

즉, local gradient인 $\frac{\partial E(\theta)}{\partial w}$, $\frac{\partial E(\theta)}{\partial b}$ 값을 계산해야합니다.

$\frac{\partial E(\theta)}{\partial w}$, $\frac{\partial E(\theta)}{\partial b}$ 값은 chain rule을 이용하여 global gradient인 $\frac{\partial E(\theta)}{\partial \hat{y}}$값을 통해 보다 쉽게 계산할 수 있습니다.

구체적으로 다음과 같이 주어진 상황을 생각해봅니다.

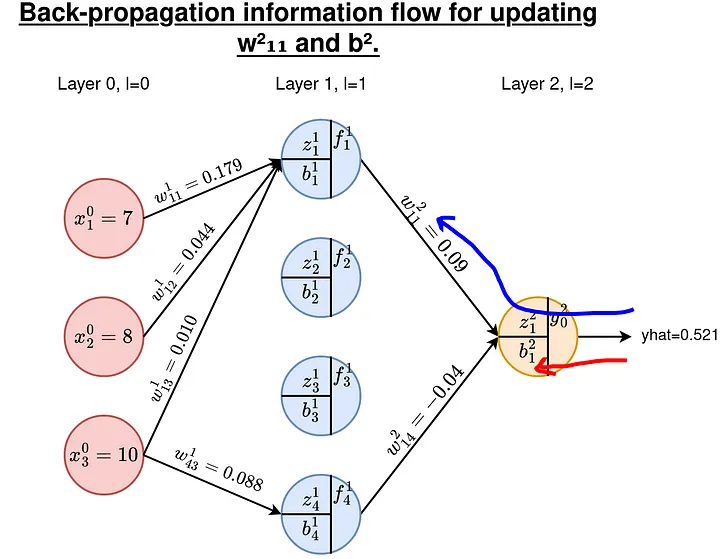https://towardsdatascience.com/how-does-back-propagation-work-in-neural-networks-with-worked-example-bc59dfb97f48

chain rule에 의해

이므로, 각 term을 구한 후 곱해서 결과값을 얻을 수 있습니다.

$\therefore$ $\frac{\partial E}{\partial w_{11}^2} = (-\frac{t}{\hat{y}} + \frac{1-t}{1-\hat{y}})((1-\hat{y})\hat{y})f_1^1$

참고문헌

• back propagation
  • https://towardsdatascience.com/how-does-back-propagation-work-in-neural-networks-with-worked-example-bc59dfb97f48