빅오 표기법
for(int i - 0; i < 10; i++){ // 10번
for(int j = 0; j < n;, J++){ // n 번
for(int k = 0; k < n; k++){ // n번
if(true) cout << i << '/n/';
}
}
}
for(int i = 0; i < n; I++){
if(true) cout << i << '/n/';
}위 코드의 시간 복잡도는 주요 로직의 반복 횟수
즉, 10 * n ^ 2 + n 이다.
이를 빅오 표기법으로 나타내면 다음과 같다.
O(n^2)빅오 표기법(Big-O notation) 이란 복잡도에 가장 영향을 많이 끼치는 항의 상수인자를 빼고 나머지 항을 없애서 복잡도를 나타내는 표기법이다.
big o complexity chart
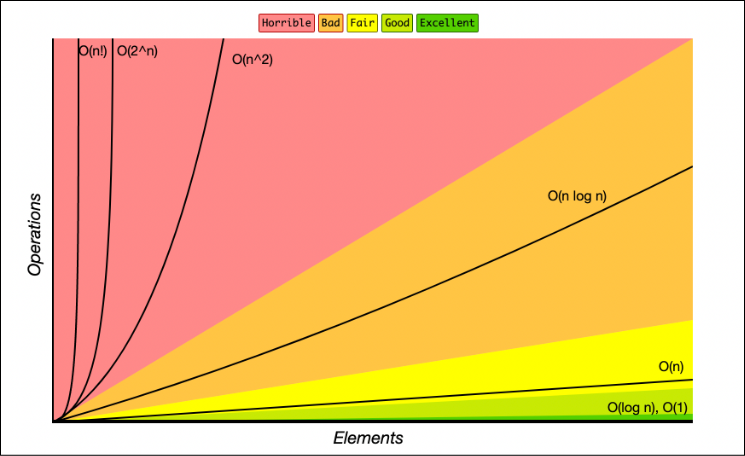
O(n!) > O(2^n) > O(n^2) > O(n log n) > O(n) > O(log n), O(1)
상수시간 시간복잡도 O(1)
상수시간 시간복잡도는 입력크기와 상관없이 일정한 시간복잡도를 가지는 것을 말하며 O(1)의 시간복잡도를 쓴다.
예를 들어 다음은 모두 O(1)의 시간복잡도를 가진다.
- 입력과 출력
ex. cidn, cout, scanf, printf
- 곱하기
- 간단한 비교 if문
- 배열의 인덱스 참조
