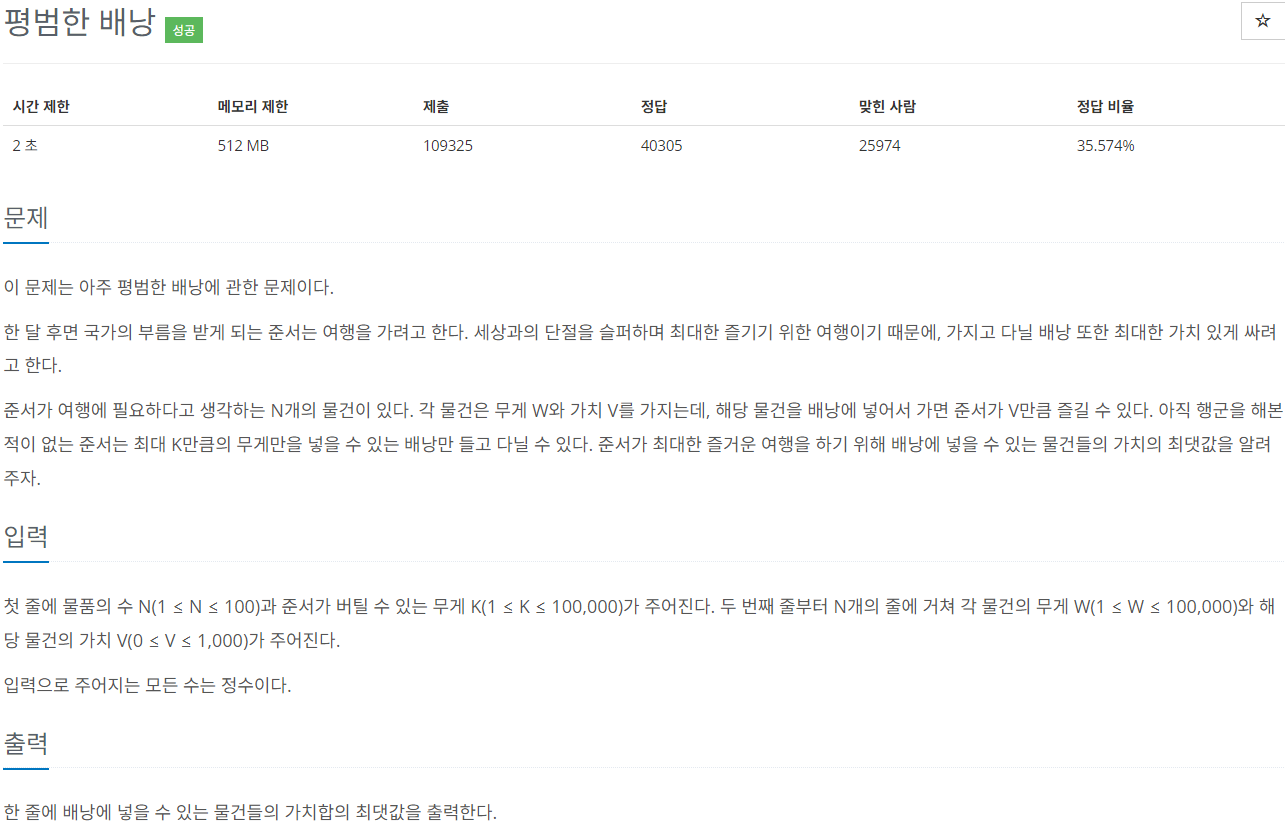
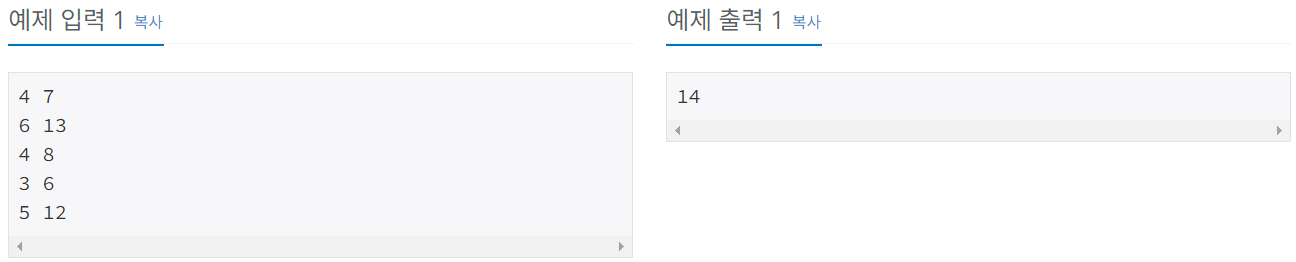
📌문제

---

📌코드

• 2차원 배열

import sys
input = sys.stdin.readline

n, k = map(int, input().split())  # 물품의 수, 최대 무게
dp = [[0] * (k + 1) for _ in range(n + 1)]

for i in range(1, n + 1):
    w, v = map(int, input().split())
    for j in range(1, k + 1):      # 용량이 j인 배낭에 i번째 물건을 넣었을 때
        if j - w >= 0:             # 이전 물건까지 살펴봤고, 배낭의 용량은 (이전 용량 - 현재 용량), 가치는 현재 가치를 더함
            # max(dp[이전 물건][현재 가방 무게], dp[이전 물건][현재 가방 - 현재 물건 무게] + 현재 물건 가치)
            dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] + v)

        else:                      # 용량이 j인 배낭에 i번째 풀건을 넣지 않았을 때
            dp[i][j] = dp[i-1][j]  # 배낭의 용량은 이전 용량 그대로, 가치는 이전 물건까지의 최댓값

print(dp[n][k])

• 1차원 배열

import sys
input = sys.stdin.readline

n, k = map(int, input().split())  # 물품의 수, 최대 무게
dp = [0] * (k + 1)

for i in range(1, n + 1):
    w, v = map(int, input().split())
    for j in range(k, 0, -1):               # 용량을 dp 배열 뒤에서부터 넣음
        if w <= j:
            dp[j] = max(dp[j], dp[j-w] + v)

print(dp[k])

---

📌풀이

• 물건의 무게와 가치
  

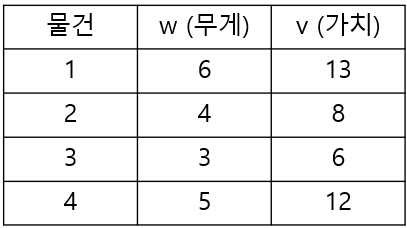
• 2차원 배열
  

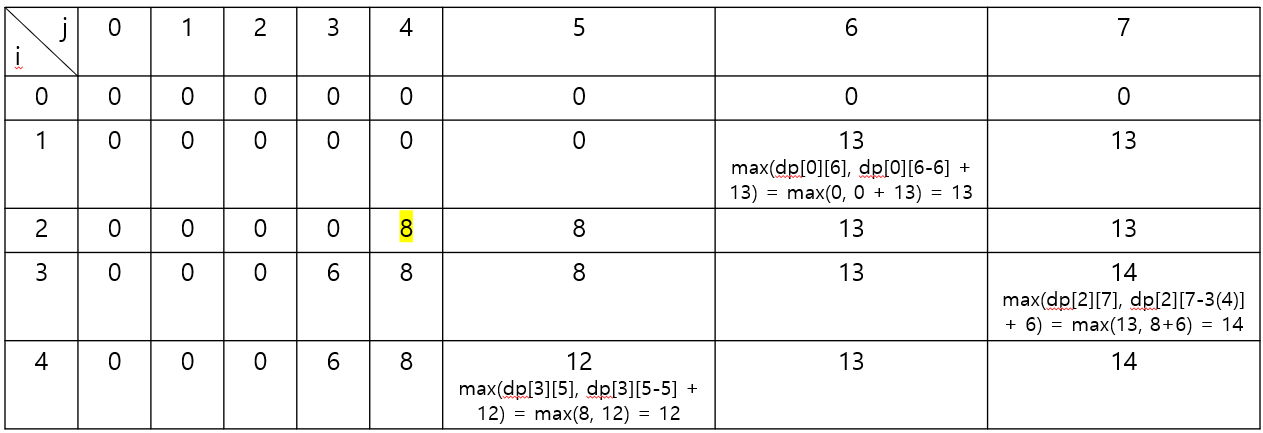
• 1차원 배열
  

# 첫번째 물건
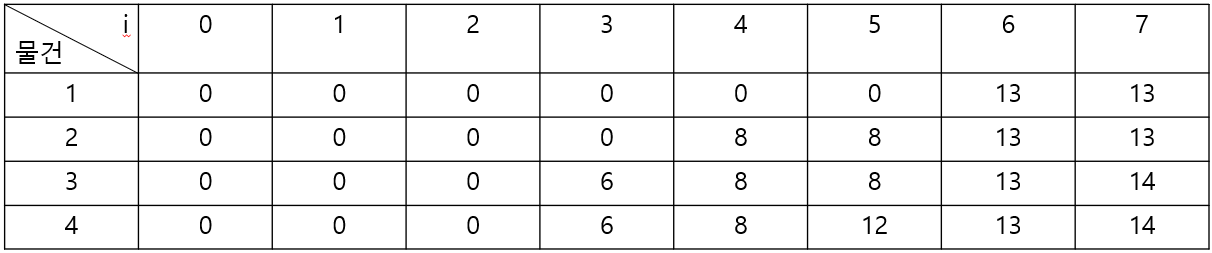
w = 6, v = 13
dp[7] = max(dp[7], dp[7 - 6] + 13) = max(0, 0 + 13) = 13
dp[6] = max(dp[6], dp[6 - 6] + 13) = max(0, 0 + 13) = 13

# 세번째 물건
w = 3, v = 6
dp[7] = max(dp[7], dp[7 - 3] + 6) = max(dp[7], dp[4] + 6) 
	  = max(13, 8 + 6) = 14

참고