
RB TREE(Red-Black)란 이진 탐색 트리(BST)의 한 종류로
스스로 균형(balancing)을 잡는 트리이다.
이진 탐색 트리는 worst case일 경우 O(n)의 시간 복잡도를 가지는데
RB Tree는 최악의 경우에도 O(logN)의 시간복잡도를 보장하는 면에서
장점을 가지고 있다.
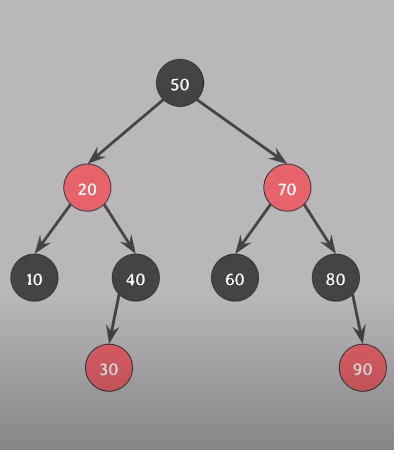
Red-Black Tree의 속성
- 모든 노드는 red 혹은 black이다.
- 루트 노드는 black이다.
- 모든 nil(leaf) 노드는 black이다.
- red의 자녀들은 black이며 red가 연속적으로 존재할 수 없다.
- 임의의 노드에서 자손 nil 노드들까지 가는 경로들의 black 수는 같다.
-> 이때, 자기 자신은 카운트에서 제외함
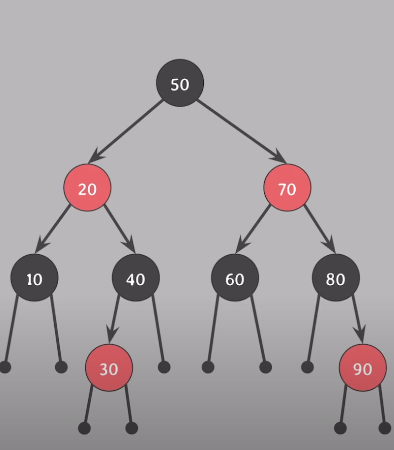
NIL 노드란?
RB tree에만 존재하는 독특한 속성
- 존재하지 않음을 의미하는 노드
- 자녀 노드가 없을 때, 자녀를 nil 노드로 표기
- 값이 있는 노드와 동등하게 취급
- RB tree에서 leaf 노드는 nil 노드
- 위 그림에서 맨 아래 검은색 점이다.
노드 x의 black height
노드 x에서 임의의 자손 nil 노드까지 내려가는 경로에서의 black의 수
-> 이때 자기 자신은 카운트에서 제외함
-> 5번 속성을 만족해야 성립하는 개념
예를 들어 20에서 10의 nil노드까지 black height를 계산해보면 2가 나오는데,
조건 5를 만족하므로 다른 경로는 볼 필요가 없다.
이와 더불어 추가적인 특징이 존재하는데,
색을 바꾸더라도 5번 속성은 유지되는 것이다.
이말은 즉슨, RB tree가 5번 속성을 만족하고 있고
두 자녀가 같은 색을 가지고 있을 때, 부모와 두 자녀의 색을 바꿔줘도
5번 속성은 여전히 만족한다는 것이다.
회전 (Rotate)
RB tree에는 회전이라는 특이한 속성이 존재한다.
void left_rotate(rbtree *t, node_t *x){
node_t *y = x->right; // y를 설정한다.
x->right = y->left; // y의 왼쪽 서브 트리를 x의 오른쪽 서브 트리로 옮긴다.
if (y->left != t->nil){
y->left->parent = x; // x의 부모를 y로 연결한다.
}
y->parent = x->parent;
if (x->parent == t->nil){
t->root = y;
}
else if (x == x->parent->left){
x->parent->left = y;
}
else{
x->parent->right = y;
}
y->left = x; // x를 y의 왼쪽으로 놓는다.
x->parent = y;
}void right_rotate(rbtree *t, node_t *y){
node_t *x = y->left;
y->left = x->right;
if (x->right != t->nil){
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == t->nil){
t->root = x;
}
else if (y == y->parent->left){
y->parent->left = x;
}
else{
y->parent->right = x;
}
x->right = y;
y->parent = x;
}RB tree 삽입
절차는 다음과 같다
- 삽입 전, RB tree 속성을 만족한 상태
- 삽입 방식은 일반적인 BST와 동일
- 삽입 후 RB tree 위반 여부를 확인
- 만약 RB tree 속성을 위반했다면 재조정
- 속성을 다시 만족
삽입하는 노드의 색은 항상 red이고 nil 노드는 black
만약 루트 노드라면 black으로 변경
node_t *rbtree_insert(rbtree *t, const key_t key) {
// TODO: implement insert
node_t *z = malloc(sizeof(node_t)); // 노드를 삽입하기 위한 노드 생성 및 메모리 할당
node_t *x = t->root;
node_t *y = t->nil;
z->key = key; // 삽입할 노드에 key값 저장
while (x != t->nil){
y = x;
x = (z->key < y->key) ? x->left : x->right;
}
z->parent = y;
if (y == t->nil){
t->root = z;
}
else{
if (z->key < y->key){
y->left = z;
}
else {
y->right = z;
}
}
z->left = t->nil;
z->right = t->nil;
z->color = RBTREE_RED;
rb_insert_fixup(t, z);
return z;
}속성을 위반하는 경우 rb_insert_fixup으로 조정한다.
void rb_insert_fixup(rbtree *t, node_t *z){
node_t *y;
// 부모가 black이라면 반복문을 거치지 않고, root를 black으로 변경 후 함수 종료
while (z->parent->color == RBTREE_RED){
if (z->parent == z->parent->parent->left){
y = z->parent->parent->right;
// case 1
// z, parent, uncle(tmp)가 모두 red일 경우
if (y->color == RBTREE_RED){
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
// 조부모를 새로운 z로 두고 while 루프를 돌면서 색을 바꿔줌.
z = z->parent->parent;
}
// case 2
else {
if (z == z->parent->right){
z = z->parent;
left_rotate(t, z);
}
// case 3
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
right_rotate(t,z->parent->parent);
}
}
else{
y = z->parent->parent->left;
// case 1
if (y->color == RBTREE_RED){
z->parent->color = RBTREE_BLACK;
y->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
}
// case 2
else {
if (z == z->parent->left){
z = z->parent;
right_rotate(t, z);
}
// case 3
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
left_rotate(t,z->parent->parent);
}
}
}
t->root->color = RBTREE_BLACK;
}RB tree 삭제
절차는 다음과 같다.
- 삽입 전, RB tree 속성을 만족한 상태
- 삽입 방식은 일반적인 BST와 동일
- 삭제 후 RB tree 위반 여부를 확인
- 만약 RB tree 속성을 위반했다면 재조정
- 속성을 다시 만족
그렇다면 속성 위반 여부는 어떻게 확인할까?
-> RB tree에서 삭제되는 노드의 색을 통해 할 수 있다
1) 만약 삭제하려는 노드의 자녀가 없거나 하나라면 삭제되는 색은
-> 삭제되는 노드의 색
2) 만약 삭제하려는 노드의 자녀가 둘이라면 삭제되는 색은
-> 삭제되는 successor의 색
-> successor는 삭제되는 노드보다 큰 노드 중에 제일 작은 노드
만약 삭제되는 색이 RED라면 어떠한 속성도 위반하지 않는다.
하지만 삭제되는 색이 BLACK일 경우 #2, #4, #5 속성을 위반할 수 있다.
int rbtree_erase(rbtree *t, node_t *p) {
// TODO: implement erase
if (p == NULL){
return 0;
}
node_t *y = p;
node_t *x; // fixed_up의 기준이 될 노드
color_t y_original_color = p->color;
// 노드의 한 자식이 nil이거나, 두개 다 nil일 경우
// 나머지 자식을 x로 두고, y를 교체한다.
// case1 : 왼쪽 노드가 nil일 경우
if (p->left == t->nil){
x = p->right;
rb_transplant(t, p, p->right);
}
// case2 : 오른쪽 노드가 nil일 경우
else if (p->right == t->nil){
x = p->left;
rb_transplant(t, p, p->left);
}
// case3 : 왼쪽 , 오른쪽 모두 nil이 아닐 경우
else{
//
//successor -> 지울 키값 보다 큰 수 중 제일 작은 값 찾기
y = p->right;
while (y->left != t->nil){
y = y->left;
}
y_original_color = y->color;
x = y->right;
// case1 : p의 자식이 y일 때
if (y->parent == p){
x->parent = y;
}
else{
// 그 외의 케이스 : y의 부모노드를 y->right와 연결해준다.
rb_transplant(t, y, y->right);
// p의 오른쪽 노드를 y와 연결한다.
y->right = p->right;
p->right->parent = y;
}
// p의 부모노드를 y와 연결한다.
rb_transplant(t,p,y);
y->left = p->left;
p->left->parent = y;
y->color = p->color;
}
// delete하며 바뀌거나 삭제된 노드의 색이 black이라면, 규칙5번 위반
// 이를 해결하기 위해, 빈 공간을 대체한 노드 x에 가상의 black을 하나 더 추가.
// 즉, 함수가 시작될 때, x는 여분의 b를 하나 더 들고 있음
if (y_original_color == RBTREE_BLACK){
RB_ERASE_FIXUP(t, x);
}
free(p);
return 0;
}
재조정은 rb_erase_fixup으로 진행한다.
void RB_ERASE_FIXUP(rbtree *t, node_t *x){
node_t *w;
// fix 시작 조건
while (x != t->root && x->color == RBTREE_BLACK){
// 기준 노드가 왼쪽에 위치할 때
if (x == x->parent->left){
w = x->parent->right;
// case1 : 삼촌 노드가 RED일 때
if(w->color == RBTREE_RED){
// 형제 노드를 검은색으로 칠한다.
w->color = RBTREE_BLACK;
// 부모노드를 빨간색으로 칠한다.
x->parent->color = RBTREE_RED;
// 부모노드를 기준으로 좌회전
left_rotate(t, x->parent);
w = x->parent->right;
}
// case2 : 삼촌노드가 두개의 BLACK 노드를 가지고 있을 경우
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK){
// 형제노드만 빨간색으로 만들고 타겟을 부모로 변경한다.
w->color = RBTREE_RED;
x = x->parent;
}
// 자식 중 하나는 빨간색일 경우
else{
// case3 : 삼촌이 BLACK이고, 왼쪽 자식이 RED, 오른쪽 자식은 BLACK일 경우
if (w->right->color == RBTREE_BLACK){
// 부모 노드의 색을 형제로 넘긴다.
w->left->color = RBTREE_BLACK;
// 부모노드와 형제 노드의 오른쪽 자식을 검은색으로 칠한다.
w->color = RBTREE_RED;
// 부모 노드 기준으로 우회전한다
right_rotate(t, w);
w = x->parent->right;
}
// case4 : 삼촌이 BLACK이고, 오른쪽 자식이 RED일 ㄷ경우
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
left_rotate(t,x->parent);
x = t->root;
}
}
// 기준이 되는 노드가 오른쪽에 위치할 때
else{
w = x->parent->left;
if (w->color == RBTREE_RED){
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t,x->parent);
w = x->parent->left;
}
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK){
w->color = RBTREE_RED;
x = x->parent;
}
else{
if (w->left->color == RBTREE_BLACK){
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w);
w = x->parent->left;
}
w->color = x->parent->color;
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t,x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}에러
-
동적으로 할당한 메모리가 제대로 해제되지 않은 이슈
==178476== total heap usage: 42 allocs, 41 frees, 2,256 bytes allocated ... ... ... ==178476== ERROR SUMMARY: 1 errors from 1 contexts (suppressed: 0 from 0)테스트 케이스는 Pass하지만, 메모리 해제가 제대로 되지 않아 에러를 발생하는 문제가 발생하였다.
void delete_rbtree(rbtree *t) {
// TODO: reclaim the tree nodes's memory
delete_node(t, t->root);
free(t->nil);
free(t);
t->nil = NULL;
t = NULL;
}다음과 같이 수정해주었다.
void delete_rbtree(rbtree *t) {
// TODO: reclaim the tree nodes's memory
delete_node(t, t->root);
free(t->nil);
t->nil = NULL;
free(t);
t = NULL;
}