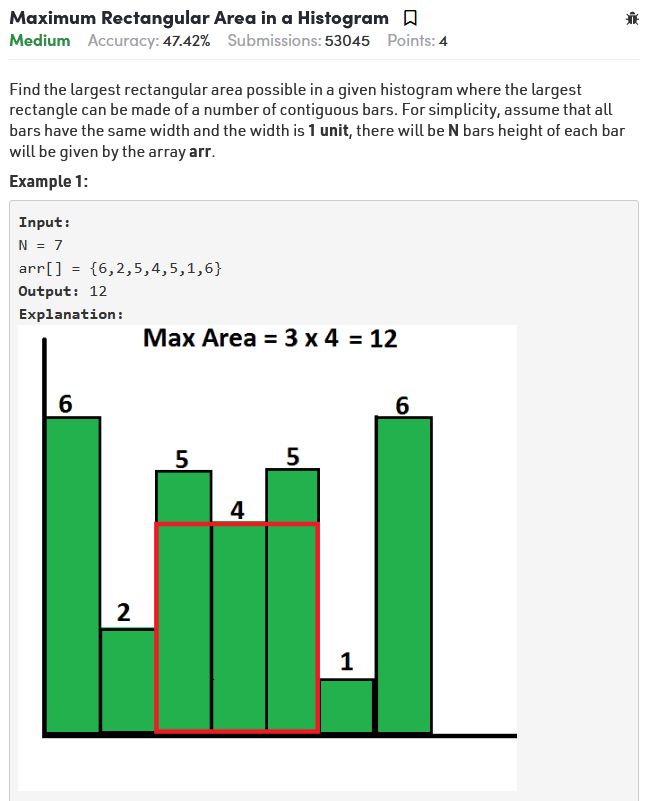
문제

https://practice.geeksforgeeks.org/problems/maximum-rectangular-area-in-a-histogram-1587115620/1#

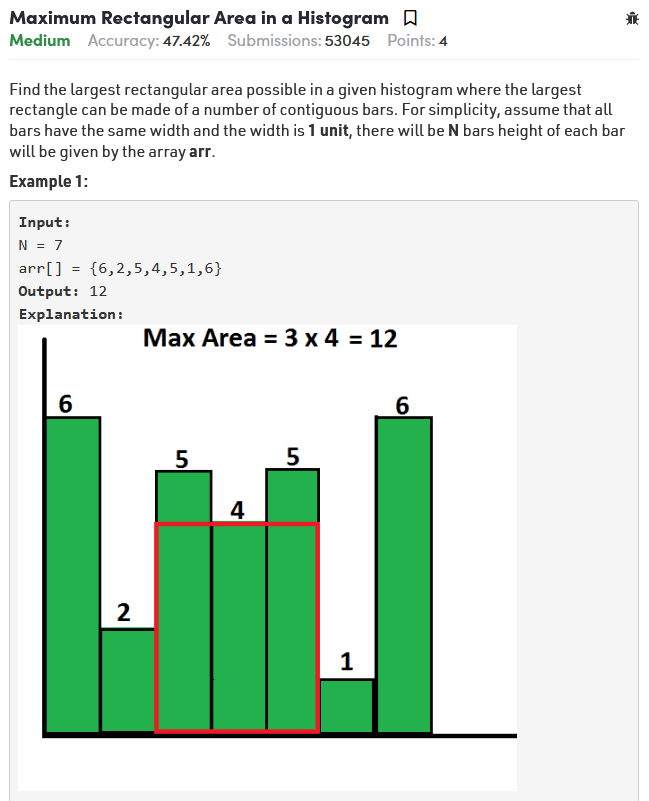
GFG 기준 Medium, 백준 기준 Platinum5에 해당하는 문제다.

접근

분할 정복

대표적인 분할 정복 문제이다.

분할 포인트를 어디에 두느냐에 따라 여러가지 방법이 있겠으나, 가운데 지점을 pivot으로 잡고 좌우로 재귀 분할 해나가는 방법이 가장 직관적으로 이해하기 쉽다.

다만 좌우로 분할해나가는 과정의 시간 복잡도가 logN이고, 좌우에서 각각 구한 것 중 더 큰 값인 부분 최대 크기와 좌우를 아우르는 너비에서 전체 최대 크기를 비교하여 최대 사이즈를 갱신하는 과정이 O(N) 시간 소요되므로, 전체 시간 복잡도는 O(NlogN)이 된다.

(1) 좌우 분할
(2) 좌우에서 각각 최대 크기 구한 후 더 큰 것 기억
(3) 위에서 구한 크기와 좌우 전체 구간에서 최대 크기를 비교하여 더 큰 것 기억

(1), (2) 까지는 구현이 어렵지 않다.
재귀로 쪼개나갈 것이기 때문에 결국 너비가 1이 될때까지 내려가서 바로 옆의 너비가 1인 다른 높이과 비교하면 되기 때문이다.

public static long getArea(long hist[], long lo, long hi){
	    
	    if(lo==hi) return 0;
	    if(lo+1 == hi) return hist[(int)lo];
	    
	    long mid = (lo+hi)/2;
	    
	    long max = Math.max(getArea(hist, lo, mid), getArea(hist, mid+1, hi));
	    
	    return max;
	    
}
    
static long getMaxArea(long hist[], long n) {
		
		long lo = 0;
		long hi = n-1;
		
		if(n==1) return hist[0];
		
		long mid = (lo+hi)/2;

		long max = Math.max(getArea(hist, lo, mid), getArea(hist, mid+1, hi));
		
		// max = Math.max(max, getLocalMaxArea(hist, lo, hi, mid));
		
		return max;
	
}

문제는 (3)인데, 좌우 중 더 큰 값이 반드시 좌우 전체의 최대 사이즈에서의 최대 크기와 동일하지 않기 때문이다.

아래 그림을 보자.

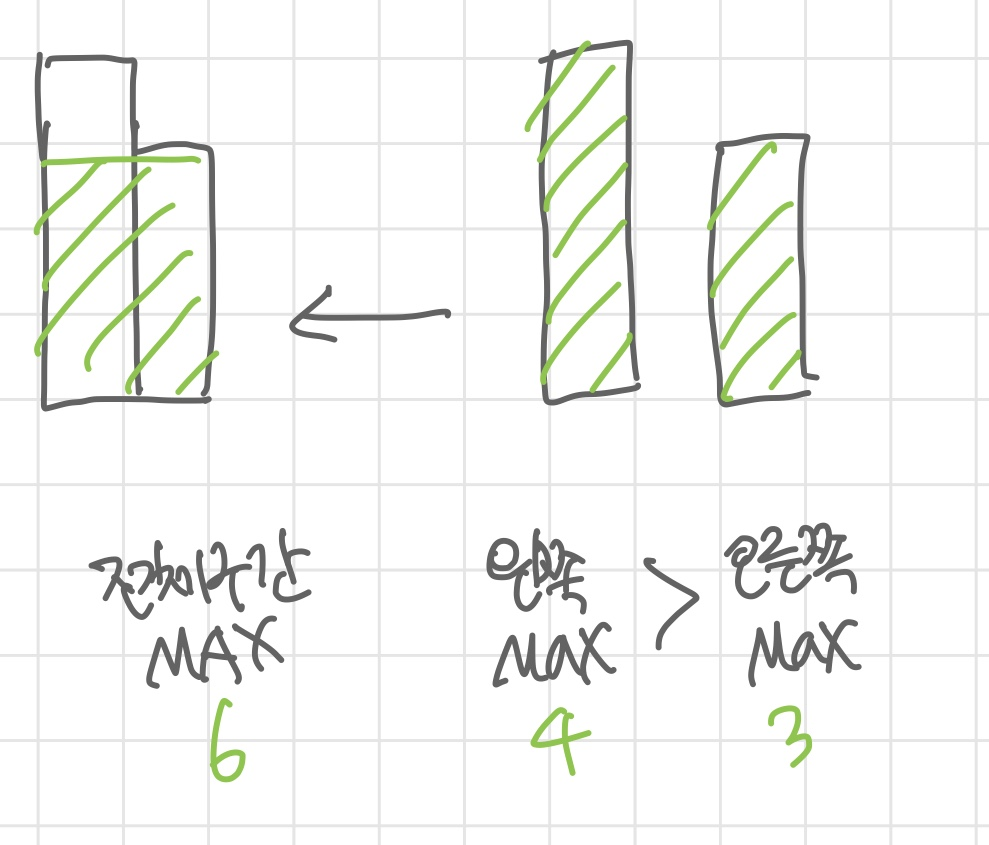
왼쪽과 오른쪽을 각각 비교할 때는 4가 제일 큰 사이즈였는데, 막상 2개를 붙여서 최대 사이즈를 구하면 6이 된다.

이걸 코드로 풀어내기 위해서 전체 사이즈에 대해 투 포인터로 탐색해나가며 최대 사이즈를 구해준다.

(1) 중간값에서 좌우 포인터 시작
(2) 중간값 기준 좌우 높이 중 더 큰 곳으로 포인터 이동, 최대 높이는 중간값과 포인터가 이동한 곳 중 더 작은 것을 기억
(3) 좌우 포인터 사이 간격을 최대 높이로 곱한 후, 그동안 구했던 사이즈보다 더 크다면 기억

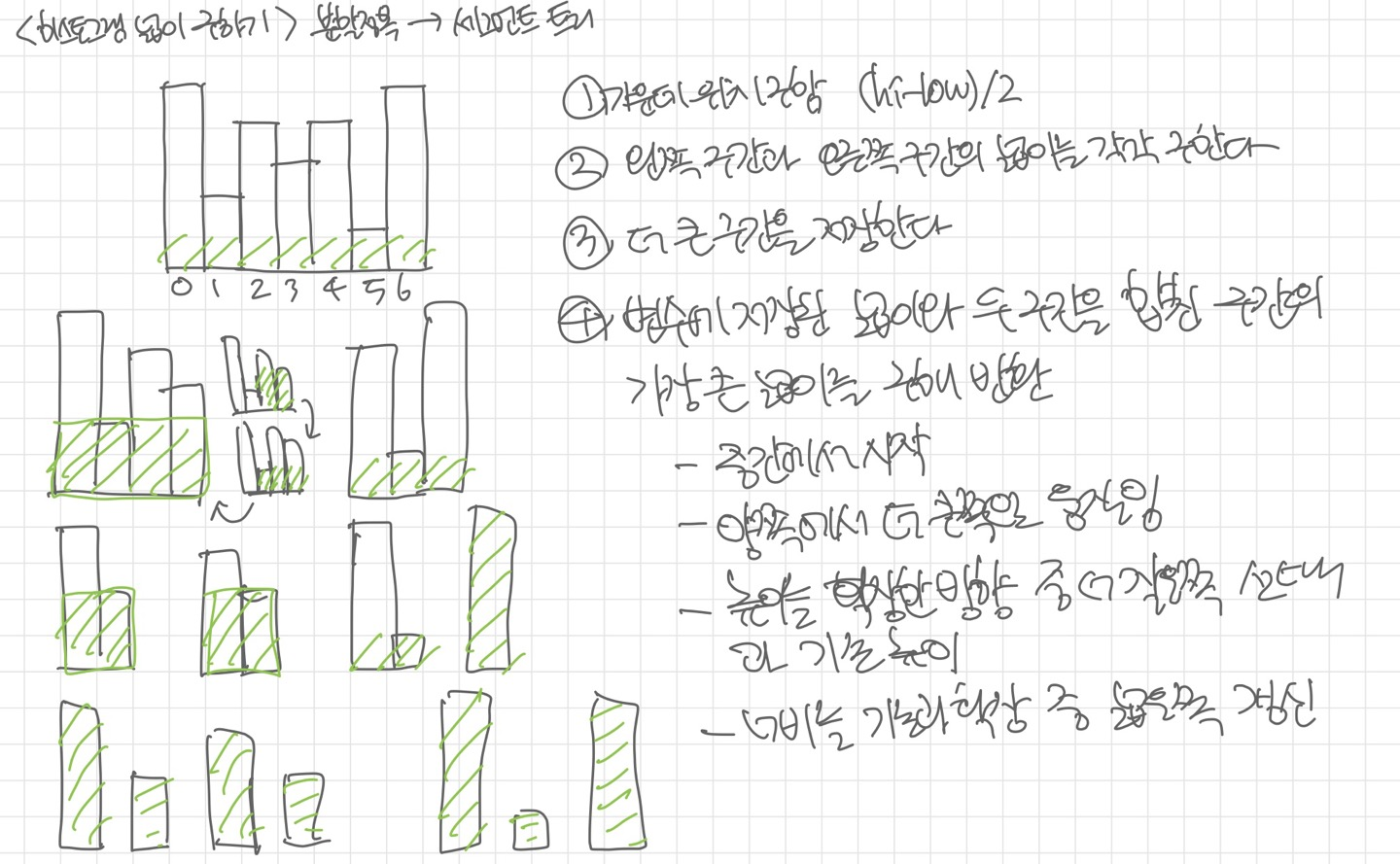
알아보기 어렵겠지만... 초록색으로 칠한 영역이 각 단계에서 얻을 수 있는 최대 크기이다.

히스토그램 문제에서 가장 중요한 팁은 직전 위치의 높이보다 현재 위치의 높이가 낮아야만, 최대 크기를 구하는 기준 높이로 삼을 수 있다 는 것이다. 가장 낮은 천장을 기준으로 크기를 구해야 한다.

위 그림에서 맨 위 히스토그램을 보면 제일 낮은 크기가 1이기 때문에 최대 사이즈가 7 밖에 안 되는 것을 알 수 있다.

따라서, 분할 정복을 해나가면서 부분 최대 크기를 갱신해야 한다. 이때 정복 단계에서 최대 높이를 구하는 기준 높이를 포인터 이동할 때마다 갱신해줘야 한다.

public static long getLocalMaxArea(long hist[], long lo, long hi, long mid){
	
		long toLeft = mid;
		long toRight = mid;
		
		long height = hist[(int)mid];
		
		long maxArea = height;
		
		while(lo<toLeft && toRight<hi){
		
			/* 좌우 중 더 높은 곳으로 이동, 최대 높이는 기존값과 옮긴 값 중 더 작은 쪽으로 갱신*/
			if(hist[(int)toLeft-1]<hist[(int)toRight+1]){
				toRight++;
				height = Math.min(height, hist[(int)toRight]);
			}
			else{
				toLeft--;
				height = Math.min(height, hist[(int)toLeft]);
			}
			
			maxArea = Math.max(maxArea, height*(toRight-toLeft+1));
		}
		
		/* 오른쪽 구간이 남았다면 */
		while(toRight < hi){
		
			toRight++;
			height = Math.min(height, hist[(int)toRight]);
			maxArea = Math.max(maxArea, height*(toRight-toLeft+1));
			
		}
		
		/* 왼쪽 구간이 남았다면 */
		while(lo < toLeft ){
		
			toLeft--;
			height = Math.min(height, hist[(int)toLeft]);
			maxArea = Math.max(maxArea, height*(toRight-toLeft+1));
		}
		
		return maxArea;
	
	}

세그먼트 트리를 사용해도 복잡도는 동일하다. (세그먼트 트리 풀이는 생략한다.)

스택

하지만 이 문제의 최적화된 풀이는 스택을 이용하는 것이다.

스택을 사용하면 복잡도를 O(N)으로 줄일 수 있다. 복잡도에서 느낌이 오듯이 배열 전체를 한 번 탐색하면서 각 구간의 최대 크기를 구하고 갱신하는 방식이다. 어떻게 이게 가능할까?

앞서 언급한 직전 위치의 높이보다 현재 위치의 높이가 낮아야만, 최대 크기를 구하는 기준 높이로 삼을 수 있다 는 성질을 그대로 사용하면 된다.

직전 높이보다 현재 높이가 더 크거나 같으면 스택에 저장하고, 직전보다 작다면 지금까지 스택에 저장된 높이 후보들을 이용해서 부분 최대 크기를 각각 구하여 스택을 비운다.

이때, 기준 높이는 스택의 top에 있던 높이 이며, 기준 높이를 곱할 너비는 최대 높이가 갱신되는 지금부터 현재 위치 전까지이다.

따라서 top을 빼내고 나서도 스택에 뭔가 남아있다면 높이 후보가 더 있다는 것이므로 그 직전부터 현재 직전까지를 너비로 삼으면 되고, 스택이 비어있다면 시작부터 현재 직전까지 하나의 높이 후보가 적용된다는 점을 이해해야 한다.

끝까지 다 돌면 스택에 최소 1개가 남게 되는데, 이 높이는 따로 구해주면 된다.

코드를 보면 다음과 같다.

 static long getMaxArea(long hist[], long n) 
    {

        Stack<Integer> s = new Stack<>();
        
        long max_area = 0; 
        int tp;  
        long area_with_top;
     
        int i = 0;
        while (i < n)
        {
            if (s.empty() || hist[s.peek()] <= hist[i])
                s.push(i++);
     
            else
            {
                tp = s.peek();  
                s.pop();  
     
                area_with_top = hist[tp] * (s.empty() ? i : i - s.peek() - 1);
     
                if (max_area < area_with_top)
                    max_area = area_with_top;
            }
        }
     
        while (s.empty() == false)
        {
            tp = s.peek();
            s.pop();
            area_with_top = hist[tp] * (s.empty() ? i : i - s.peek() - 1);
     
            if (max_area < area_with_top)
                max_area = area_with_top;
        }
     
        return max_area;

    }

설명에 영 소질이 없는 것 같은데.. 요즘 마음이 급해서 더 대충 쓰게 된다 ㅜㅜ

히스토그램 문제를 풀 때는 스택 혹은 투 포인터 를 이용하면 대부분 풀린다.

하지만 확장해 나갈 때 어떤 동작을 할 건지는 문제마다 통찰력이 필요하며 이때 분할 정복 논리가 적용되는 경우가 많다.

따라서 분할 정복 과정 중에서도 정복 시 메커니즘을 정확히 이해하는 것이 필요하고, 속도 최적화를 위해 이걸 스택으로 비틀어서 풀이하면 최상의 해결이 되겠다.