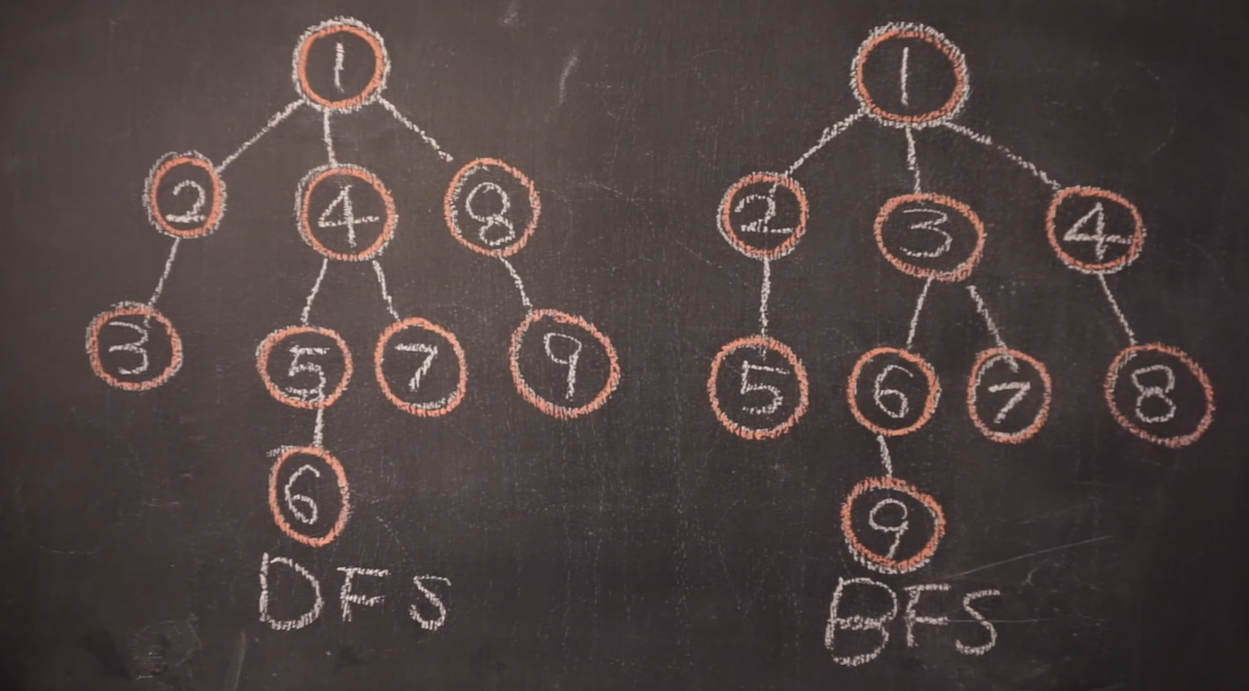
1. 깊이 우선 탐색 (DFS, Depth-First Search)
DFS는 Stack 자료구조를 사용한 그래프 탐색 알고리즘이고 임의의 노드에서 시작하여 다른 branch로 넘어가기 전, 현재 탐색 중인 branch를 완벽하게 탐색하는 방식이다.
스택을 사용하는 이유는 가장 깊은 노드까지 도달하였을 때 탐색한 경로를 역추적하여 되돌아나오기 위함이다. 또한, 이미 방문한 노드를 다시 방문하지 않기 위해 방문한 노드를 별개로 저장하는데 이를 '방문 처리'라고 한다.
DFS의 동작 순서
- 루트 노드를 스택에 넣고 방문처리 한다.
- 스택 최상단 노드의 인접 노드 중 방문하지 않은 노드 하나를 스택에 넣고 방문처리 한다. 만약 인접 노드를 모두 방문한 경우 스택을 Pop 한다.
- 2단계를 더이상 수행할 수 없을 때까지 (스택이 빌 때까지) 반복한다.
1-1. graph와 visited 선언
graph와 visited를 선언하는 방법에는 여러가지가 있다.
그 중 2차원 리스트로 그래프 자료구조를 구현했다.
이 예제는 그래프를 입력 받는 경우가 아니라 미리 알고 있는 경우
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [0] * len(graph)1-2. 재귀를 통한 구현(DFS)
재귀를 사용하는 주된 이유는 코드의 가독성이 높아지기 때문이다. 재귀 함수 호출도 내부적으로 살펴보면 스택 메모리를 사용하기 때문에 근본적으로 동일하다고 볼 수 있다.
def dfs(graph, node, visited):
print(node, visited)
visited[node] = 1
for neighbor in graph[node]:
if visited[neighbor] == 0:
dfs(graph, neighbor, visited)
dfs(graph, 1, visited)1-3. 스택을 통한 구현 (DFS)
stack.append(1)
visited[1] = 1
while len(stack) > 0:
current_node = None
for node in graph[stack[-1]]:
if visited[node] == 0:
current_node = node
break
if current_node == None:
stack.pop()
else:
visited[current_node] = 1
stack.append(current_node)
print(visited)2. 너비 우선 탐색 (BFS, Breadth-First Search)
BFS는 큐 자료구조를 사용한 그래프 탐색 알고리즘으로 현재 노드와 가까운 노드를 우선적으로 넓게 탐색하는 방식이다.
현재 노드의 이웃 노드를 큐에 집어 넣어 먼저 들어간 노드를 먼저 탐색(FIFO)하게 되는 방식이다.
BFS 동작 순서
- 루트 노드를 큐에 넣고 방문처리한다.
- 큐를 popleft하고, popleft한 노드의 방문하지 않은 모든 인접 노드를 큐에 append한 뒤 방문처리 한다.
- 2단계를 더 이상 수행할 수 없을 때까지 (큐가 빌 때까지) 반복한다.
2-1. 구현
from collections import deque
deq = deque()
visited = [0] * len(graph)
deq.append(1)
visited[1] = 1
print(1)
while deq:
current_node = deq.popleft()
for neighbor in graph[current_node]:
if visited[neighbor] == 0:
print(neighbor)
deq.append(neighbor)
visited[neighbor] = 1