1. Graph

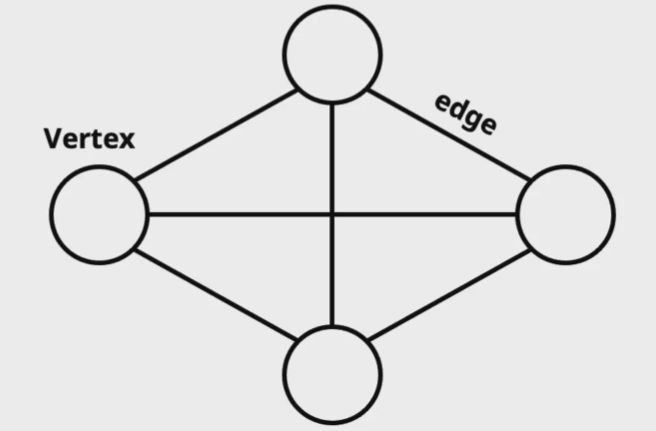
그래프는 정점(node 또는 vertex)과 간선(edge)로 이루어진 자료구조이다.

• 정점(Vertex or Node): 데이터를 저장하는 위치
• 간선(Edge): 정점(노드)를 연결하는 선. 링크(Link) 또는 브랜치(branch) 로도 불린다.

1-1. 종류

무방향 그래프

• 무방향 그래프는 두 정점을 연결하는 간선에 방향이 없는 그래프이다.
  

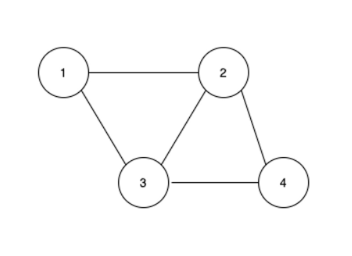
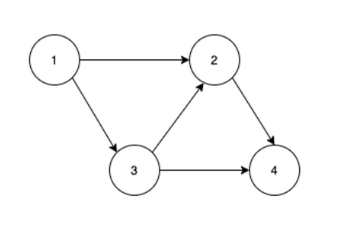
방향 그래프

• 방향 그래프는 두 정점을 연결하는 간선에 방향이 존재하는 그래프이다.
• 간선이 가리키는 방향으로만 이동할 수 있다.
  

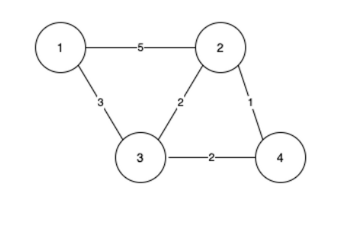
가중치 그래프

• 가중치 그래프는 두 정점을 이동할 때, 비용이 드는 그래프이다.
  

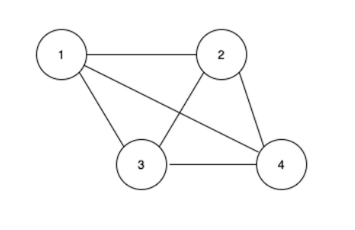
완전 그래프

• 완전 그래프는 모든 정점이 간선으로 연결된 그래프이다.
  

1-2. 그래프 구현 방법

그래프는 인접 행렬 또는 인접 리스트 로 구현할 수 있다.

1. 인접 행렬

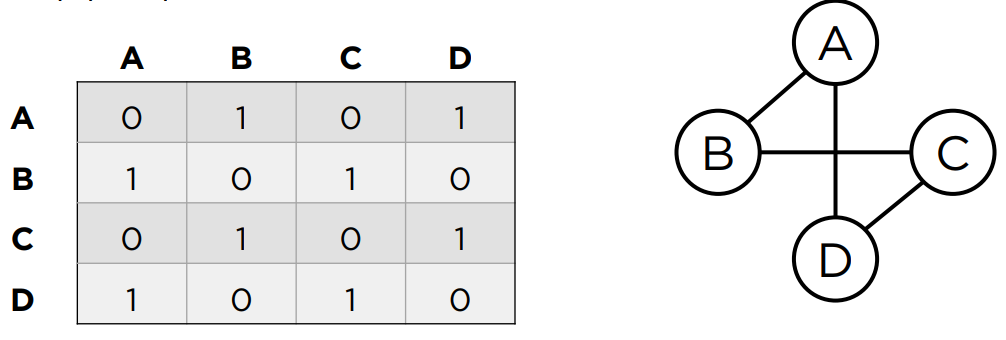
• 인접 행렬이란 그래프의 정점을 2차원 배열로 만든 것이다.
• 정점 간에 직접 연결되어 있다면 1, 아니라면 0을 저장한다.

장점

• 2차원 배열에 모든 정점의 간선 정보가 담겨있기 때문에 두 정점에 대한 연결을 조회할 때는 O(1) 의 시간 복잡도를 가진다.
• 인접 리스트에 비해 구현이 쉽다.

단점

• 모든 정점에 대해 간선 정보를 입력해야 하므로 인접 행렬을 생성할 때는 O(n^2)의 시간 복잡도가 소요된다.
• 항상 2차원 배열이 필요하므로 필요 이상의 공간이 낭비된다.

2. 인접 리스트

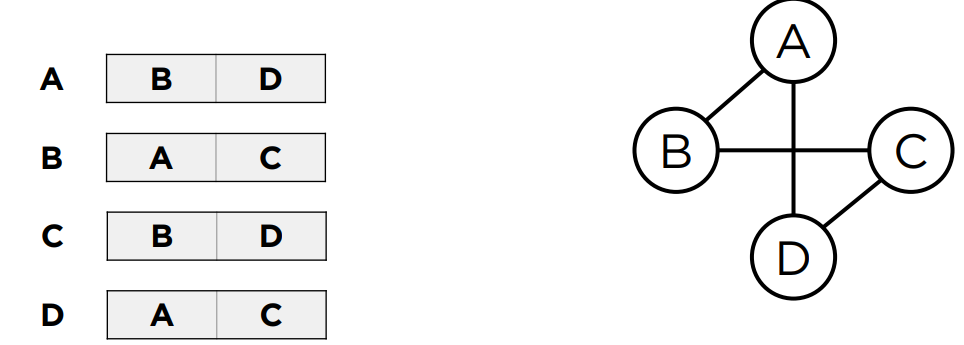
• 인접 리스트는 그래프의 노드를 리스트로 표현한 것이다. 주로 정점의 리스트 배열을 만들어서 관계를 설정한다.

장점

• 정점들의 연결 정보를 탐색할 때 O(n) 시간 복잡도가 소요된다. (n 은 간선의 갯수)
• 필요한 만큼 공간을 사용하기 때문에 인접 행렬에 비해 상대적으로 공간의 낭비가 적다.

단점

• 특정 두 정점이 연결되어 있는지 확인하기 위해서는 인접 행렬에 비해 시간이 오래 걸린다.
• 구현이 인접 행렬에 비해 어렵다.

1-3. 그래프 구현

1. 인접 행렬

AdjacencyMatrixGraph

package com.example.datastructure.Graph;

import java.util.*;

public class AdjacencyMatrixGraph implements IGraph {
    private Integer[][] matrix;
    private Set<Integer> vertexes;
    private Map<Integer, Integer> indegrees;

    public AdjacencyMatrixGraph(int numOfVertex) {
        this.vertexes = new HashSet<>();
        this.indegrees = new HashMap<>();
        this.matrix = new Integer[numOfVertex][];
        for (int i = 0; i < numOfVertex; i++) {
            this.matrix[i] = new Integer[numOfVertex];
        }
    }

    @Override
    public void add(int from, int to, Integer distance) {
        vertexes.add(from);
        vertexes.add(to);
        int count = indegrees.getOrDefault(to, 0);
        indegrees.put(to, count + 1);
        matrix[from][to] = distance;
    }

    @Override
    public void add(int from, int to) {
        vertexes.add(from);
        vertexes.add(to);
        int count = indegrees.getOrDefault(to, 0);
        indegrees.put(to, count + 1);
        matrix[from][to] = 1;
    }

    @Override
    public Integer getDistance(int from, int to) {
        return this.matrix[from][to];
    }

    @Override
    public Map<Integer, Integer> getIndegrees() {
        return this.indegrees;
    }

    @Override
    public Set<Integer> getVertexes() {
        return this.vertexes;
    }

    @Override
    public List<Integer> getNodes(int vertex) {
        List<Integer> ret = new ArrayList<>();
        for (int i = 0; i < matrix[vertex].length; i++) {
            if (matrix[vertex][i] != null) {
                ret.add(i);
            }
        }
        return ret;
    }
}

2. 인접 리스트

AdjacencyListGraph

package com.example.datastructure.Graph;

import java.util.*;

public class AdjacencyListGraph implements IGraph {

    private List<List<Node>> graph;
    private Set<Integer> vertexes;
    private Map<Integer, Integer> indegrees;

    public AdjacencyListGraph(int numOfVertex) {
        this.vertexes = new HashSet<>();
        this.indegrees = new HashMap<>();
        this.graph = new ArrayList<>(numOfVertex);
        for (int i = 0; i < numOfVertex; i++) {
            this.graph.add(new ArrayList<>());
        }
    }

    @Override
    public void add(int from, int to, Integer distance) {
        vertexes.add(from);
        vertexes.add(to);
        int count = indegrees.getOrDefault(to, 0);
        indegrees.put(to, count + 1);
        List<Node> neighbors = this.graph.get(from);
        neighbors.add(new Node(from, to, distance));
    }

    @Override
    public void add(int from, int to) {
        vertexes.add(from);
        vertexes.add(to);
        int count = indegrees.getOrDefault(to, 0);
        indegrees.put(to, count + 1);
        List<Node> neighbors = this.graph.get(from);
        neighbors.add(new Node(from, to));
    }

    @Override
    public Integer getDistance(int from, int to) {
        for (Node node : this.graph.get(from)) {
            if (node.to.equals(to)) {
                return node.weight;
            }
        }
        return -1;
    }

    @Override
    public Map<Integer, Integer> getIndegrees() {
        return this.indegrees;
    }

    @Override
    public Set<Integer> getVertexes() {
        return this.vertexes;
    }

    @Override
    public List<Integer> getNodes(int vertex) {
        List<Integer> nodes = new ArrayList<>();
        for (Node node : this.graph.get(vertex)) {
            nodes.add(node.to);
        }
        return nodes;
    }

    private class Node {
        Integer from;
        Integer to;
        int weight;

        Node(int from, int to) {
            this.from = from;
            this.to = to;
            this.weight = 1;
        }

        Node(int from, int to, int weight) {
            this.from = from;
            this.to = to;
            this.weight = weight;
        }

    }
}

1-4. 그래프 탐색

• 하나의 정점에서 시작하여 그래프의 모든 정점들을 한 번씩 방문(탐색)하는 것이 목적입니다.
• 그래프의 데이터는 배열처럼 정렬이 되어 있지 않기에, 원하는 자료를 찾으려면, 하나씩 모두 탐색해야한다.

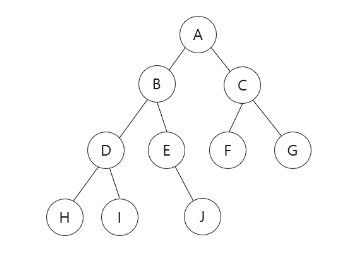
해당 그래프가 있다고 하자.

1. 넓이 우선 탐색(BFS)

• 루트 노드부터 시작하여 그래프에서 너비를 우선적으로 탐색한다.
• 큐 (Queue)를 이용한다.
  • 큐는 선입선출 (FIFO, First In First Out)
  • 큐는 수평 구조로 볼 수 있고, 수평 구조는 너비를 가진다고 할 수 있다.
• 그래프를 순차적으로 방문할 수 있어야 하고, 방문한 노드들은 다시 탐색할 일이 없도록 방문 처리되어야 한다.

A B C D E F G H I J 순으로 탐색한다.

1-1. 구현

    public static List<Integer> bfs(IGraph graph, int from) {
        // 최종 아웃풋 결과를 출력하기 위한 list
        List<Integer> result = new ArrayList<>();
        // 방문했던 vertex, node 를 재방문 하지 않기 위해 set 에 방문했던 노드 저장
        Set<Integer> visited = new HashSet<>();
        // bfs 를 위한 queue
        IQueue<Integer> queue = new MyLinkedQueue<>();
        visited.add(from);
        queue.offer(from);  // from 부터 시작
        while (!queue.isEmpty()) {  // 큐가 빌 때까지
            Integer next = queue.poll();
            result.add(next);   // 큐에서 노드를 꺼내오면서 방문
            for (Integer n : graph.getNodes(next)) {
                if (!visited.contains(n)) {
                    visited.add(n);
                    queue.offer(n);
                }
            }
        }
        return result;
    }

2. 깊이 우선 탐색(DFS)

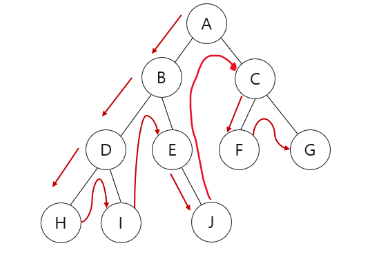
• 스택 또는 재귀 방식을 이용하여 구현할 수 있다.
  • 스택은 FILO(First-In, Last-Out) 방식

    A B D H I E J C F G 순으로 탐색한다.

2-1. 구현

public static List<Integer> dfs(IGraph graph, int from) {
        List<Integer> result = new ArrayList<>();
        Set<Integer> visited = new HashSet<>();
        IStack<Integer> stack = new MyStack<>();
        visited.add(from);
        stack.push(from);
        while (stack.size() > 0) {
            Integer next = stack.pop();
            result.add(next);
            for (Integer n : graph.getNodes(next)) {
                if (!visited.contains(n)) {
                    visited.add(n);
                    stack.push(n);
                }
            }
        }
        return result;
    }

3. 위상정렬

• 위상 정렬(Topological sort)은 비순환 방향 그래프(DAG)에서 정점을 선형으로 정렬하는 것입니다.
• 그래프가 DAG가 아닌 경우 그래프에 대한 위상 정렬은 불가능합니다.
• 구현 방법에는 in_degree를 사용하는 BFS(Breath First Search) 방법과 DFS(Depth First Search)를 사용하는 방법이 있다.

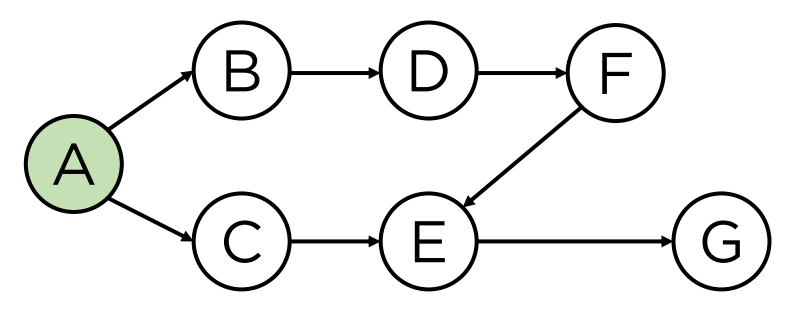
3-1. In-degree 방법(BFS 방법)

• 진입차수(indegree): 한 노드에 들어오는 다른 간선의 수

1. 모든 vertex 의 indegree 수를 센다.
2. 큐에 indegree 가 0 인 vertex 삽입
3. 큐에서 vertex 를 꺼내 연결된(나가는 방향) edge 제거
4. 3번으로 인해 indegree 가 0 이 된 vertex 를 큐에 삽입
5. 큐가 빌 때까지 3-4 반복

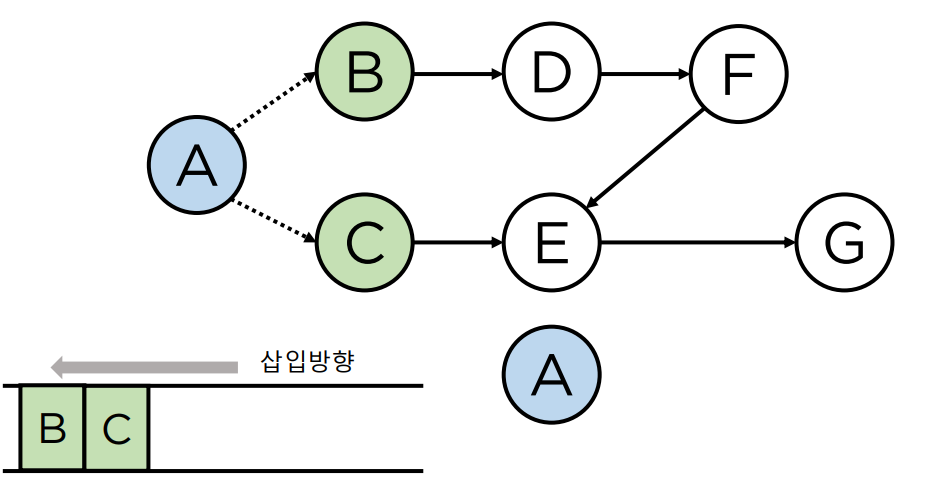
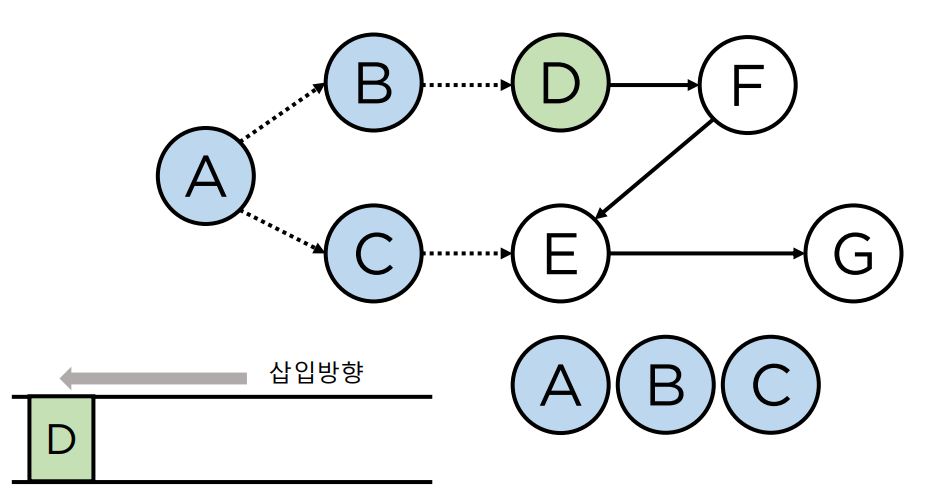
• E는 indegree가 0이 아니기 때문에 추가 되지 않음
• 반복

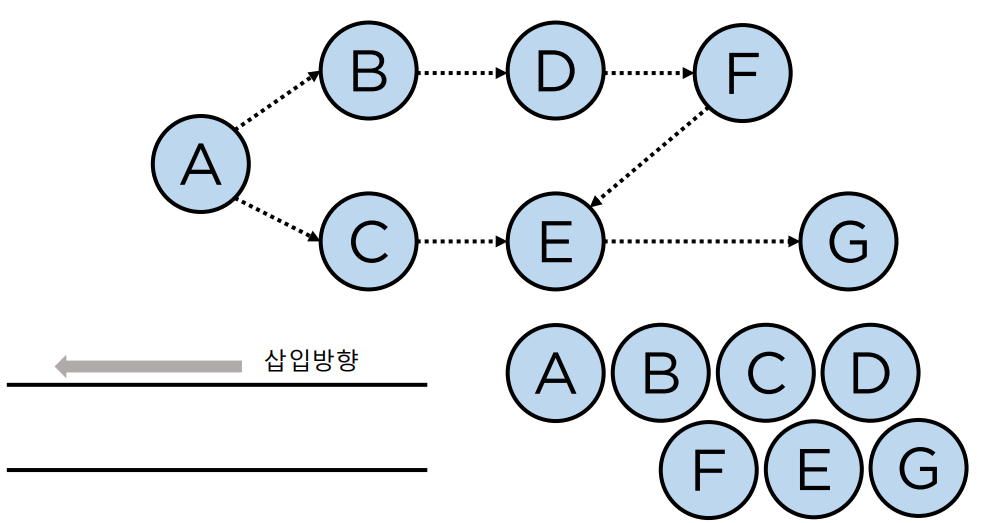
A B C D F E G 순으로 탐색

3-2. DFS(Depth First Search)방법

• DFS는 in_degree가 필요 없고 재귀를 사용합니다.
• Stack 사용

1. 하나의 정점에서 시작
2. 방문표시를 하면서 간선을 따라 다음 정점으로 방문
3. 더 이상 방문할 간선이 없으면 리스트 앞에 정점을 추가
   역추적(backtracking)을 통해 이전 정점으로 이동하면서 방문하지 않은 간선이 있는지 확인합니다.
4. 방문 가능한 간선이 있다면 다시 간선을 따라 다음 정점으로 이동
5. 모든 정점을 탐색할 때까지 2~4를 반복

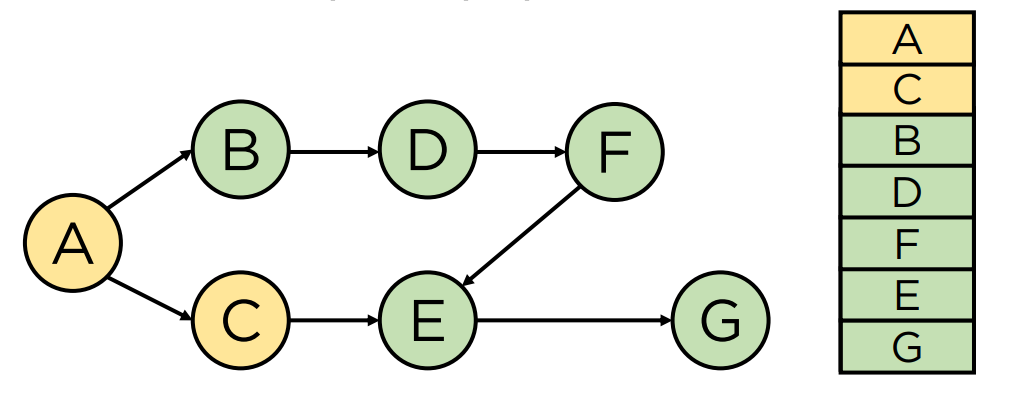
3-3. 구현

    // 1. 모든 vertax의 indegree 수를 센다
    // 2. 큐에 indegree가 0인 vertax 삽입
    // 3. 큐에서 vertex를 꺼내 연결된(나가는 방향) edge 제거
    // 4. 3번으로 인해 indegree가 0이 된 vertex를 큐에 삽입
    // 5. 큐가 빌 때까지 3~4 반복

    // queue 를 이용한 진입차수 방식
    public static List<Integer> topologicalSortIndegree(IGraph graph) {
        Map<Integer, Integer> indegreeCounter = graph.getIndegrees();
        IQueue<Integer> queue = new MyLinkedQueue<>();
        List<Integer> ret = new LinkedList<>();
        for (int v : graph.getVertexes()) {
            int count = indegreeCounter.getOrDefault(v, 0);
            if (count == 0) {
                queue.offer(v);
            }
        }

        while (!queue.isEmpty()) {
            int node = queue.poll();
            ret.add(node);
            for (int nn : graph.getNodes(node)) {
                if (indegreeCounter.containsKey(nn)) {
                    int count = indegreeCounter.get(nn);
                    if (count - 1 == 0) {
                        queue.offer(nn);
                    }
                    indegreeCounter.put(nn, count - 1);
                }
            }
        }
        return ret;
    }

    // stack 구현
    public static List<Integer> topologicalSort(IGraph graph) {
        List<Integer> result = new ArrayList<>();
        IStack<Integer> stack = new MyStack<>();
        Set<Integer> visited = new HashSet<>();
        Set<Integer> vertexes = graph.getVertexes();
        for (Integer vertex : vertexes) {
            if (!visited.contains(vertex)) {
                topologicalSort(graph, vertex, visited, stack);
            }
        }

        while (stack.size() > 0) {
            result.add(stack.pop());
        }
        return result;
    }

    private static void topologicalSort(IGraph graph, int vertex, Set<Integer> visited, IStack<Integer> stack) {
        visited.add(vertex);
        List<Integer> nodes = graph.getNodes(vertex);
        for (Integer n : nodes) {
            if (!visited.contains(n)) {
                topologicalSort(graph, n, visited, stack);
            }
        }

        stack.push(vertex);
    }

4. 다익스트라

• 다익스트라(dijkstra) 알고리즘은 그래프에서 한 정점(노드)에서 다른 정점까지의 최단 경로를 구하는 알고리즘 중 하나이다.
• 이 과정에서 도착 정점(노드) 뿐만 아닌, 다른 정점까지 최단 경로로 방문하여 각 정점까지의 최단 경로를 모두 찾게 된다.
• 매번 최단 경로의 정점을 선택해 탐색을 반복한다.
• 그래프 알고리즘 중 최단 거리, 최소 비용을 구하는 알고리즘은 다익스트라 외에 벨만-포드 알고리즘, 프로이드 워샬 알고리즘 등이 있다.

과정
1. 출발 노드와 도착 노드를 설정한다.
2. '최단 거리 테이블'을 초기화한다.
3. 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고, 방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택한다. 그 노드를 방문 처리한다.
4. 해당 노드를 거쳐 다른 노드로 넘어가는 간선 비용(가중치)을 계산해 '최단 거리 테이블'을 업데이트한다.
5. 3~4의 과정을 반복한다.

4-1. 구현

우선순위 큐

    // 다익스트라 최단거리 알고리즘
    // src 출발 노드
    // dst 도착 노드
    // return 출발 노드로부터 도착 노드까지의 최단 거리
    public static int dijkstraShortestPath(IGraph graph, int src, int dst) {
        int size = 0;
        for (int n : graph.getVertexes()) {
            if (size < n) {
                size = n;
            }
        }
        
        int[] dist = new int[size + 1];
        for (int i = 0; i < dist.length; i++) {
            dist[i] = Integer.MAX_VALUE;
        }

        dist[src] = 0;
        PriorityQueue<Pair> pq = new PriorityQueue<>();
        pq.add(new Pair(src, 0));

        while (!pq.isEmpty()) {
            Pair top = pq.poll();
            if (dist[top.vertex] < top.distance) {
                continue;
            }
            for (int node : graph.getNodes(top.vertex)) {
                if (dist[node] > dist[top.vertex] + graph.getDistance(top.vertex, node)) {
                    dist[node] = dist[top.vertex] + graph.getDistance(top.vertex, node);
                    pq.add(new Pair(node, dist[node]));
                }
            }
        }
        return dist[dst];
    }

    private static class Pair implements Comparable<Pair> {
        int vertex;
        int distance;

        public Pair(int vertex, int distance) {
            this.vertex = vertex;
            this.distance = distance;
        }

        @Override
        public int compareTo(Pair o) {
            return distance - o.distance;
        }
    }