[알고리즘] 구현, DFS&BFS

방예서·2022년 7월 31일

자료구조와 알고리즘

목록 보기

2/2

구현

머릿속 알고리즘을 소스코드로 바꾸는 과정.
주로 시뮬레이션과 완전 탐색의 유형을 말한다.

일반적으로 알고리즘 문제에서의 2차원 공간은 행렬이고, 방향 벡터가 자주 사용된다.

// 동북서남
let dx = [0, -1, 0, 1];
let dy = [1, 0, -1, 0];

//현재 위치
let x = 2;
let y = 2;

for (let i=0; i<4; i++) {
  //다음 갈 수 있는 모든 위치 (동북서남으로)
  let nx = x + dx[i];
  let ny = y + dy[i];
  console.log(nx, ny);
}

재귀 함수

자기 자신을 다시 호출하는 함수이다.
재귀 함수를 사용할 경우에는 반드시 재귀 함수의 종료 조건을 명시해야한다.

팩토리얼


// 반복으로 구현

const factorial1 = (n) => {
  let result = 1;
  
  for (let i=1; i<=n; i++) result *= i;
  return result;
}

const factorial2 = (n) => {
  if (n <= 1) return 1;
  return n * factorial2(n-1);
}

최대공약수 계산

유클리드 호제법이란?
두 자연수 A, B에 대해 (A>B) A를 B로 나눈 나머지를 R이라고 한다.
이때 A, B의 최대공약수 === B, R의 최대공약수


const gcd = (a, b) => {
  if (a % b === 0) return b;
  else return gcd(b, a % b);
}

재귀 함수 유의사항

모든 재귀 함수는 반복문을 이용하여 동일한 기능 구현이 가능하다.
컴퓨터는 함수를 연속적으로 호출 시 컴퓨터 메모리 내부의 스택 프레임에 쌓인다. 그래서 스택을 사용해야 할 때, 구현상 스택 라이브러리 대신 재귀 함수를 이용하는 경우가 있다.

DFS & BFS

대표적인 그래프 탐색 알고리즘이다.

그래프를 표현하는 방식

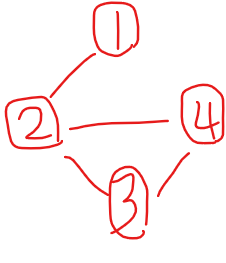
인접 행렬

/	1	2	3	4
1	0	1	0	0
2	1	0	1	1
3	0	1	0	1
4	0	1	1	0

인접 리스트

1 : [2]
2 : [1, 3, 4]
3 : [2, 4]
4 : [2, 3]

DFS

깊이 우선 탐색으로, 그래프의 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
스택 자료구조(혹은 재귀 함수)를 이용한다.

탐색 시작 노드를 스택에 삽입하고 방문 처리
인접한 노드부터 방문(여러 개면 숫자 작은 노드)
스택의 최상단 노드에 방문하지 않은 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문
방문하지 않은 인접한 노드가 없으면 스택에서 최상단 노드 꺼냄
2번의 과정을 반복할 수 없을 때까지 반복

DFS 구현

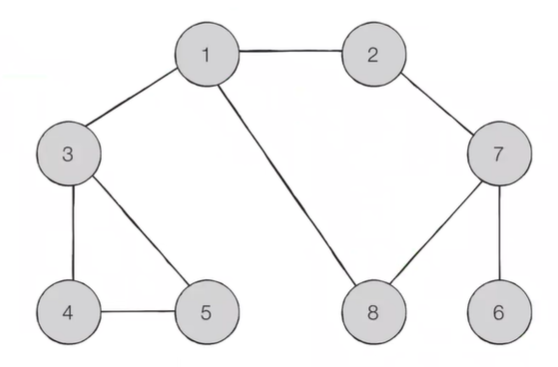
인접리스트로 표시하여 DFS를 구현해보면


// v는 현재 노드 위치(인덱스)
const dfs = (graph, v, visited) => {
  // 현재 노드 방문 처리
  visited[v] = true;
  console.log(v);
  // 현재 노드와 인접한 다른 노드들을 재귀적으로 방문
  for (i of graph[v]) {
    // 방문한 적 없는 노드
    if (!visited[i]) {
      dfs(graph, i, visited);
    }
  }
};

// 모든 배열의 첫 인덱스는 '0'이기 때문에 없는 것처럼 처리
const graph = [
  [],
  [2, 3, 8],
  [1, 7],
  [1, 4, 5],
  [3, 5],
  [3, 4],
  [7],
  [2, 6, 8],
  [1, 7],
];

let visited = Array(9).fill(false);

dfs(graph, 1, visited);

BFS

너비 우선 탐색으로, 그래프에서 가장 가까운 노드부터 탐색하는 알고리즘이다.
큐 자료구조(선입선출)를 이용한다.

탐색 시작 노드를 스택에 삽입하고 방문 처리
큐에서 노드를 꺼낸 뒤(가장 먼저 들어왔던 노드) 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입, 방문 처리
2번의 과정을 반복할 수 없을 때까지 반복

BFS 구현

인접리스트로 표시하여 BFS를 구현해보면

const bfs = (graph, start, visited) => {
  let queue = [];
  queue.push(start);
  // 현재 노드 방문 처리
  visited[start] = true;
  // 큐가 빌 때까지 반복
  while (queue.length != 0) {
    // 큐에서 원소 뽑아서 출력 (선입선출)
    let v = queue.shift();
    console.log(v);
    // 아직 방문하지 않은 인접 원소들 큐에 삽입
    for (i of graph[v]) {
      if (!visited[i]) {
        queue.push(i);
        visited[i] = true;
      }
    }
  }
};

// 모든 배열의 첫 인덱스는 '0'이기 때문에 없는 것처럼 처리
const graph = [
  [],
  [2, 3, 8],
  [1, 7],
  [1, 4, 5],
  [3, 5],
  [3, 4],
  [7],
  [2, 6, 8],
  [1, 7],
];

let visited = Array(9).fill(false);

bfs(graph, 1, visited);