문제
입력
첫 번째 줄에 문제의 개수N(1<=N<=100)과 제한 시간 M(10<=M<=1000)이 주어집니다.
두 번째 줄부터 N줄에 걸쳐 문제를 풀었을 때의 점수와 푸는데 걸리는 시간이 주어집니다.
출력
첫 번째 줄에 제한 시간안에 얻을 수 있는 최대 점수를 출력합니다.
정답 풀이
- 여기서 중요한 조건이 나왔다. "한 유형당 한문제만 풀 수 있다는 것"
이는 대부분 이차원 리스트로 풀라고 하지만, 냅색알고리즘을 M부터 즉, 마지막 부터 돌면 굳이 이차원 리스트로 풀지 않을 수 있다. 코멘트에 이차원 리스트로 푸는 법을 남겨 놓겠지만, 일차원 리스트로 풀어서 메모리를 줄이고 속도를 올리자.
이런 리스트에서 M부터 기준이 되는 값까지 초기화 한다,
다음 for문을 돌고 또 이미 초기화 한 값을 참조하여 max를 정한다.
반복...
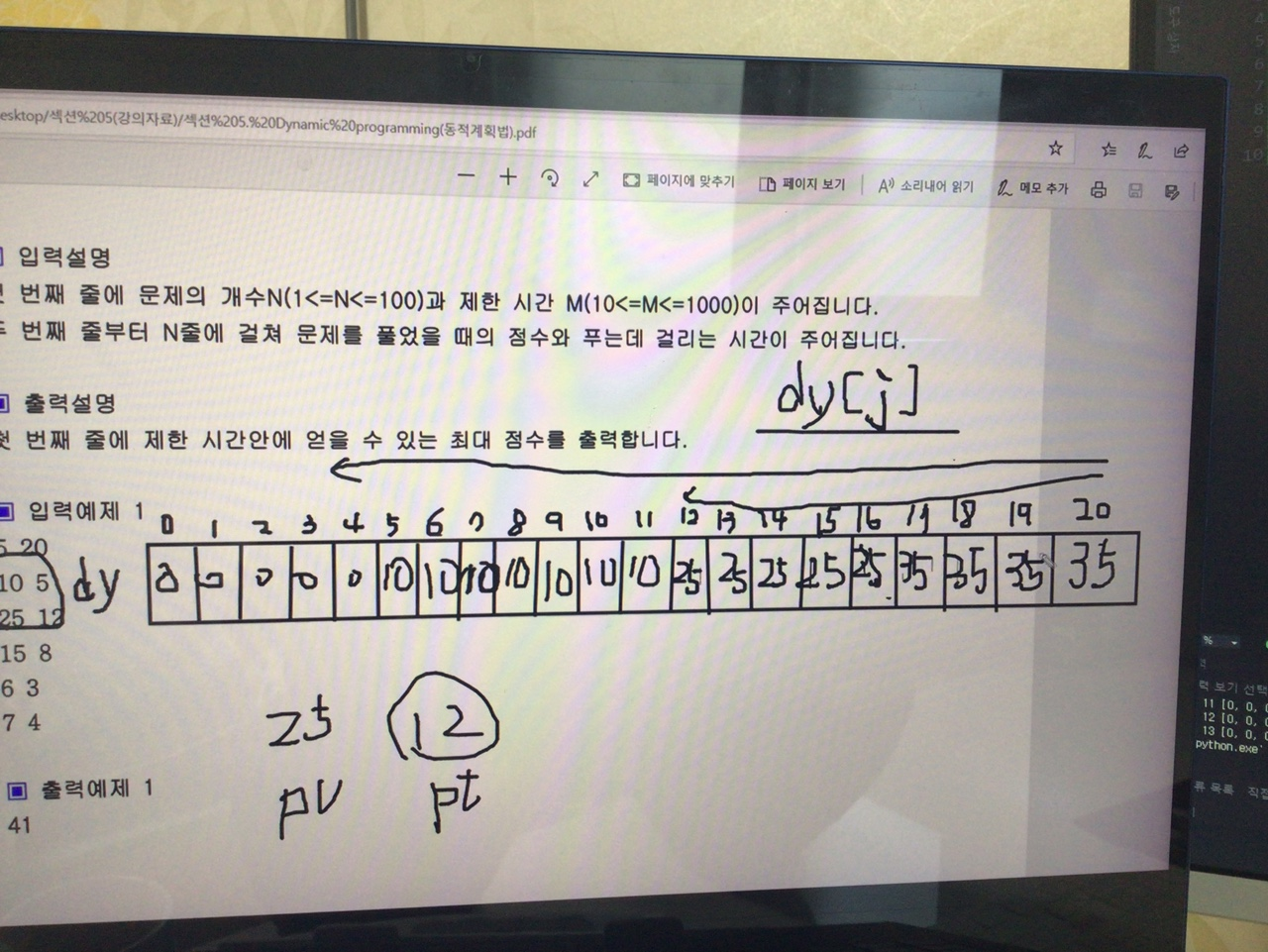
pv에는 현재 점수를 저장하고
pt에는 현재 시간을 저장한다
그럼 이전에 max시켰던 값과 비교해서 일차원 배열을 초기화 할 수 있다.
dy[j] = max(dy[j], dy[j-pt]+ps)
그럼 이렇게 된다.
정답 코드
import sys
sys.stdin = open ("input.txt", "rt")
def input():
return sys.stdin.readline().rstrip()
if __name__ == "__main__":
N, M = map(int,input().split())
# M = timelimit
dy = [0]*(M+1)
# 한 유형당 한개만 풀수 있다는 조건이 있음!!! 따라서 이차원 테이블을 사용해야 한다.
# 하지만 이렇게 이차원으로 하다보면 용량이 어마무시하게 커진다. 속도도 느려진다. 따라서 실전에서는 일차원으로 설명해라.
for i in range(N):
ps, pt=map(int,input().split())
for j in range(M, pt-1, -1):
dy[j] = max(dy[j], dy[j-pt]+ps)
print(dy[M])
코멘트
이차원 리스트로 중복 없는 냅색 알고리즘 풀기
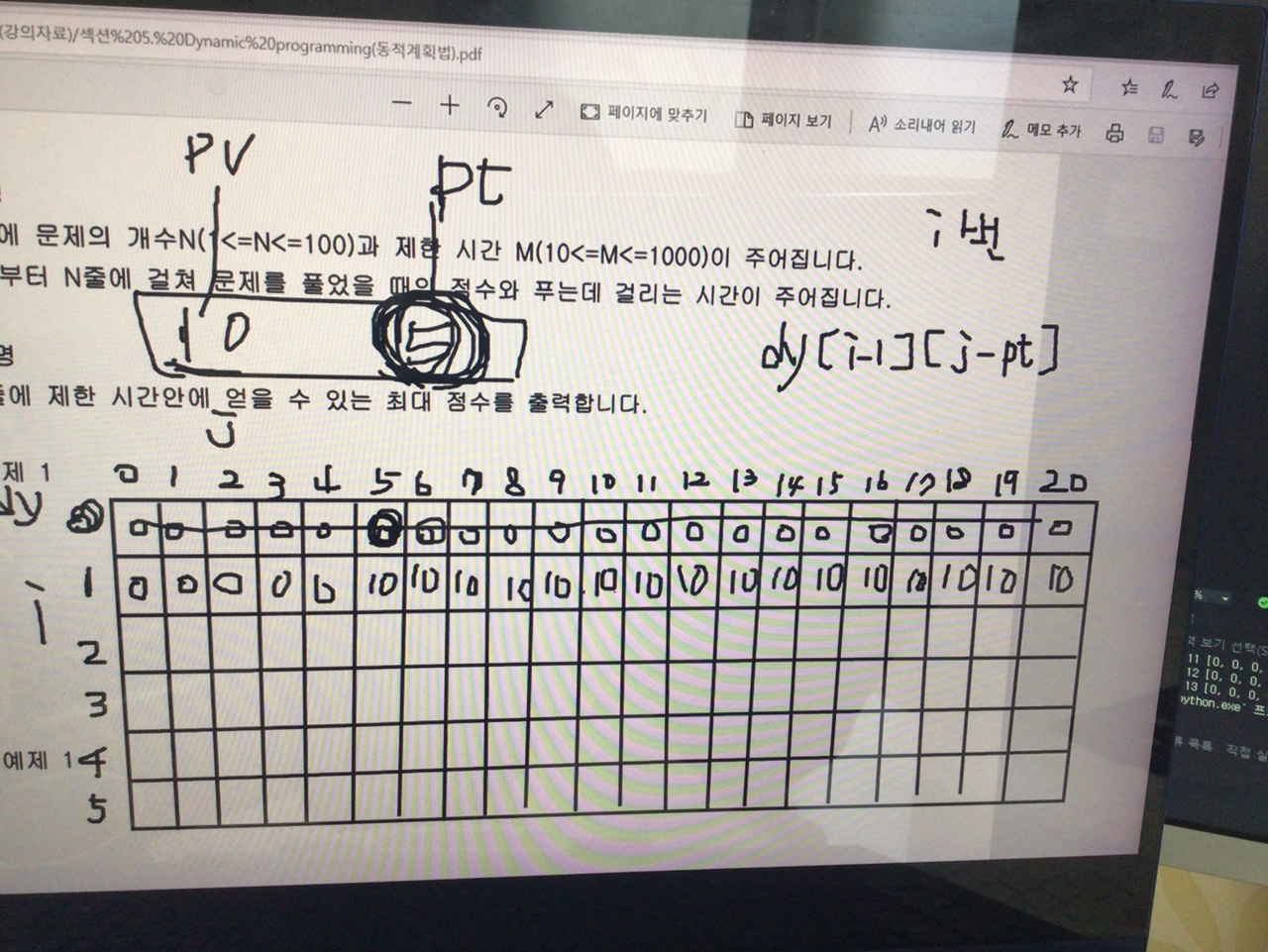
알고리즘은 결국 dy[i-1][j-pt] 즉, 이전에 초기화 된 i-1번째 배열에서 값을 참조한다.
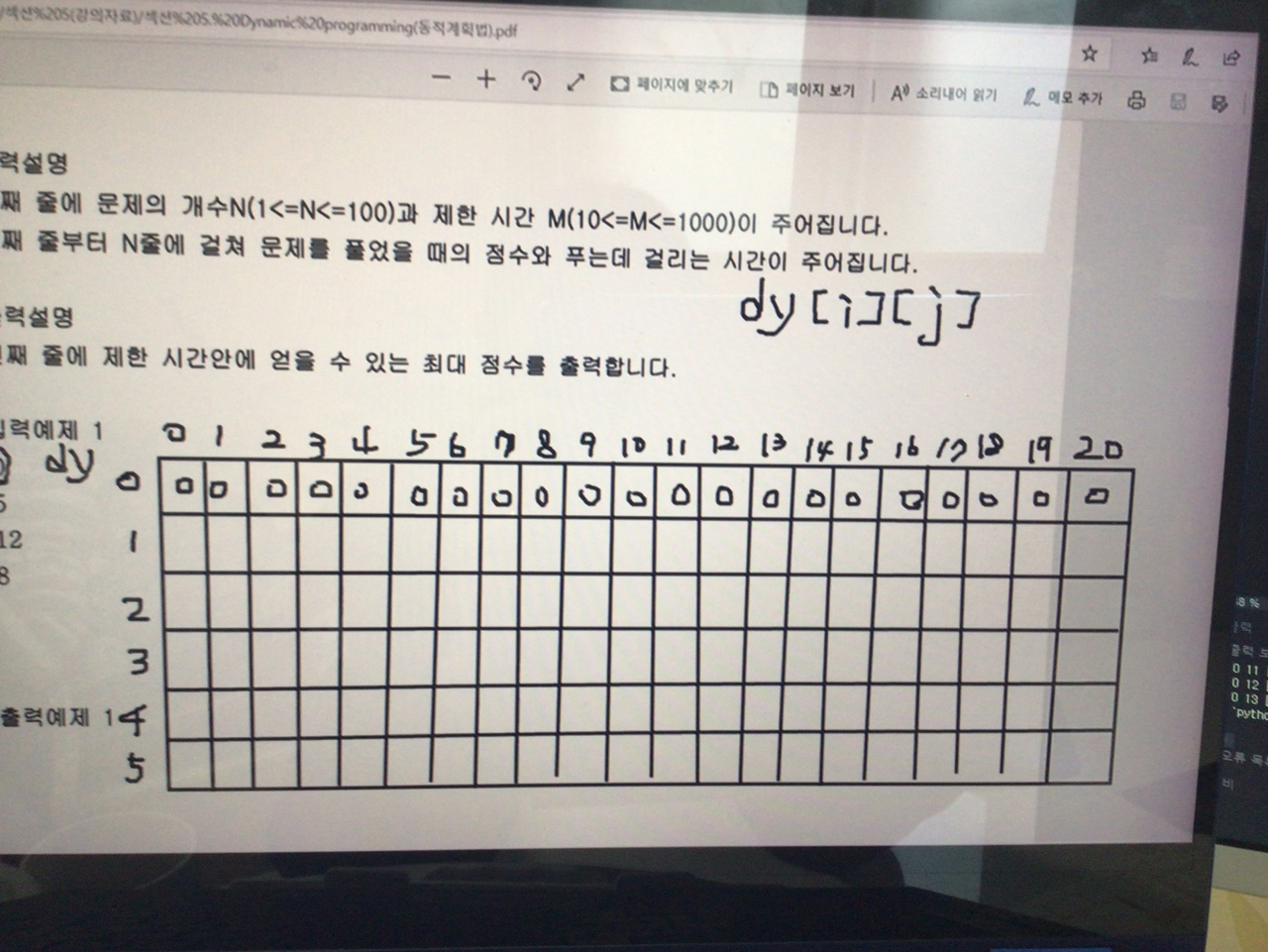
처음 0번째 행에는 모두 0으로 초기화
이후에 for문 돌면서 score 초기화

이전행에 기록해놓은 최댓값을 참조하여 계속 초기화 해 나가면된다.
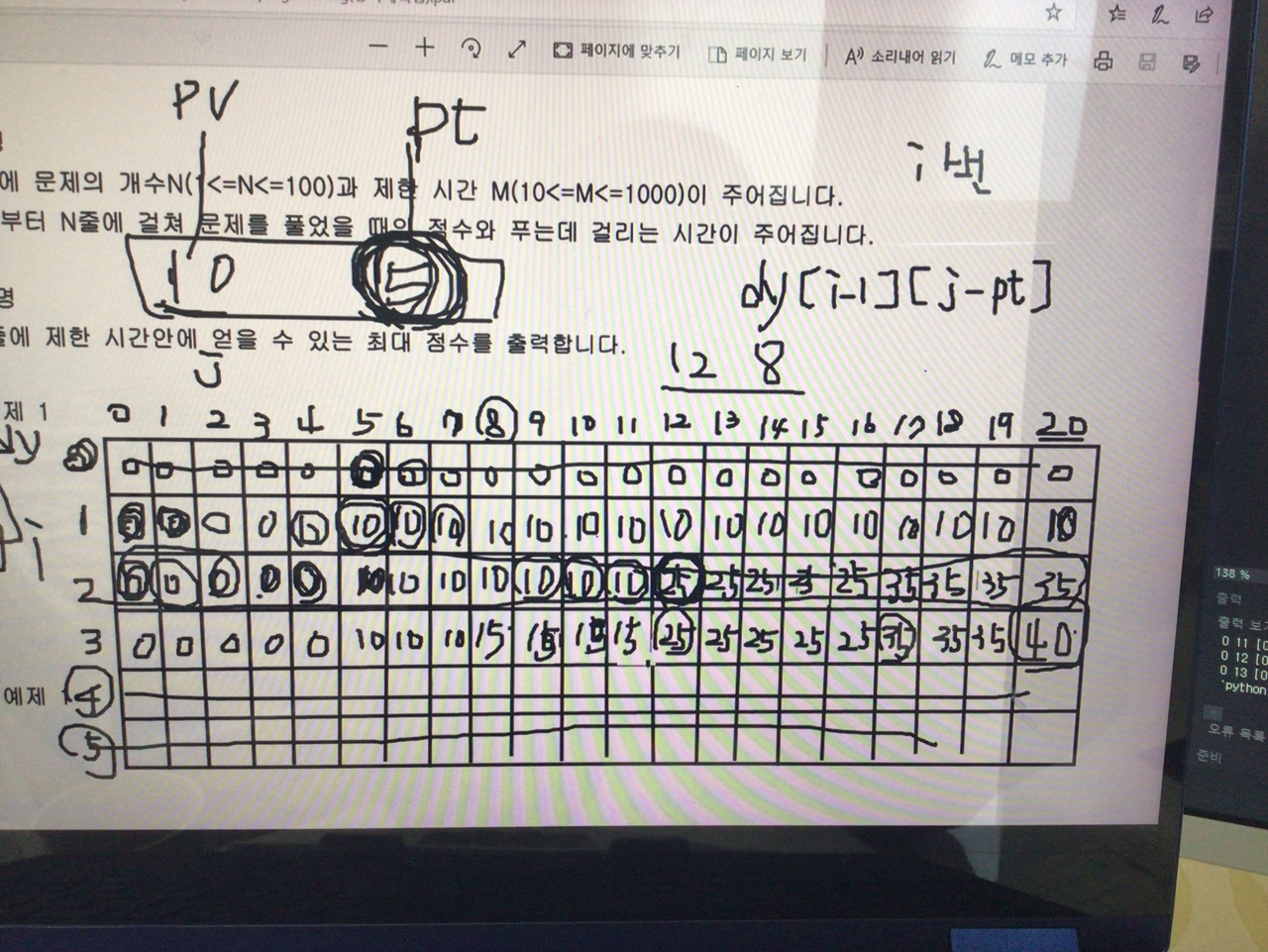
메모리 많이 잡아먹는 방법이라 결국에는 앞서 보여줬던
일차원 리스트를 거꾸로 도는 방식이 좋다 !