GCD와 LCM

GCD

최대공약수(Greatest Common Divisor, GCD)는 두 수 이상의 여러 공약수 중 최대인 수를 가리킨다.

• 공약수(Common Divisor)
  : 최대공약수의 개념 중 공약수는 두 수 이상의 여러 수 중 공통된 약수를 의미한다.
• 약수(Divisor)
  : 어떤 수를 나누어떨어지게 하는 수를 의미한다.

LCM

최소공배수(Lowest Common Multiple, LCM)은 두 수 이상의 여러 공배수 중 최소인 수를 가리킨다.

• 공배수(Common Multiple)
  최소공배수의 개념 중 공배수는 두 수 이상의 여러 수 중 공통된 배수를 의미한다.
• 배수(Multiple)는 하나의 수에 정수를 곱한 수이다. 반대로 말해서, 배수는 그 수에 의해 나누어 떨어지는 수라고 볼 수 있다.

GCM과 LCM을 구하는 방식

1. 작은 수들의 곱으로 나타내며 구하는 방법
   
2. 공약수로 나누어보며 구하는 법
   
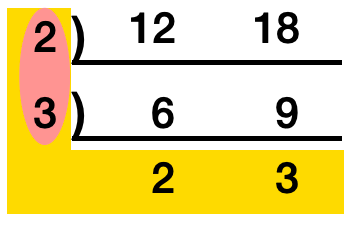
   12와 18을 더이상 나눌 수 없는 수까지 나눕니다. 여기서 나누는 데에 사용된 수인 2와 3을 곱하면 6이 나오고, 이 6은 최대공약수가 된다. 그리고 나누는 데에 사용된 수와 더 이상 나눌 수 없는 수들을 곱하게 되면 36이 나오고, 이 수는 최소공배수가 된다.
   

3. 유클리드 호제법

유클리드 호제법

유클리드 호제법은 최대공약수와 관련이 깊은 공식이다.

2개의 자연수 a와 b가 있을 때, a를 b로 나눈 나머지를 r이라 하면 a와 b의 최대공약수는 b와 r의 최대공약수와 같다는 이론이다. 이러한 성질에 따라 b를 r로 나눈 나머지 r’를 구하고, 다시 r을 r’로 나누는 과정을 반복해, 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수임을 알 수 있게 된다.

단 a가 b보다 커야 한다는 조건(절대적 조건)이 있다. 왜냐하면 나누었을 때 음수가 나오면 안 되기 때문이다.

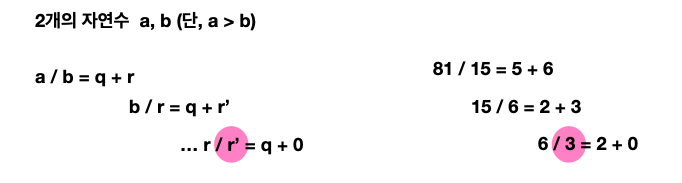
유클리드 호제법을 이용하게 되면 최대공약수를 쉽게 구할 수 있게 되고, 최대공약수를 구할 수 있게 되면 최소공배수는 자연스럽게 구할 수 있게 된다.

코드-최대공약수

function gcd(a, b){
	while(b !== 0){
		let r = a % b;
		a = b;
		b = r;
	}
	return a;
}

코드-최소공배수

function lcm(a, b){
	return a * (b / gcd(a, b));
}

해당 함수 lcm 은 마찬가지로 a와 b를 매개변수로 받고 있으며, 리턴되는 값으로 a에 b를 최대공약수로 나눈 값을 곱하고 있다. 여기서 최대공약수의 값은 위에서 만들었던 함수 gcd를 이용해 구할 수 있다.

최소공배수는 최대공약수를 이용해서 만들어지는 수입니다. 그러므로 최대공약수를 만들 줄 알면 최소공배수 또한 만들 수 있게 된다.