모각소 2주차 활동내용
7월 15일 오후 3시부터 시작한 SCPC 1차 예선이 끝난 뒤 모각소 친구들과 풀이를 공유하고 어려웠던 문제를 같이 생각해봤다. 코드는 부분점수만 맞았고 2번 문제까지밖에 제대로 못 풀었기 때문에 생략하고 어떻게 접근했는지에 대한 설명만 간단하게 서술하겠다.
문제는 아직 SCPC에서 공개하지 않았기 때문에 출처는 없는 상태이다.
1번 개미
문제: 개미가 정해진 위치에서 짐을 들고 일렬로 나란히 서있을 때, 짐의 무게 순서대로 정렬하고자 한다. 이때 개미1의 위치가 A에서 B로 이동했다면 B-A만큼 이동거리가 증가한다.
개미를 짐의 무게 순서대로 정렬했을 때 개미들 이동거리의 합이 최소가 되는 값을 출력하라
입력) 첫 줄에 개미들의 위치들을 입력, 두번 째 줄에 개미들이 들고있는 짐의 무게를 입력한다.
출력) 최소의 이동거리값을 출력한다.
예시 입력) 예시 출력)
1 2 4 6 8 14
9 2 2 1 2
풀이) 먼저 이 문제는 sort 알고리즘을 이용해서 풀어야겠다 생각했고 짐은 무게 순서대로 정렬해야하기 때문에 1 2 2 2 9로 정렬될 것이다. 그리고 2 2 2 셋이 최소로 움직이기 위해선 "8 위치"에 있던 "2의 짐"을 든 개미가 "6 위치"로 이동해야한다
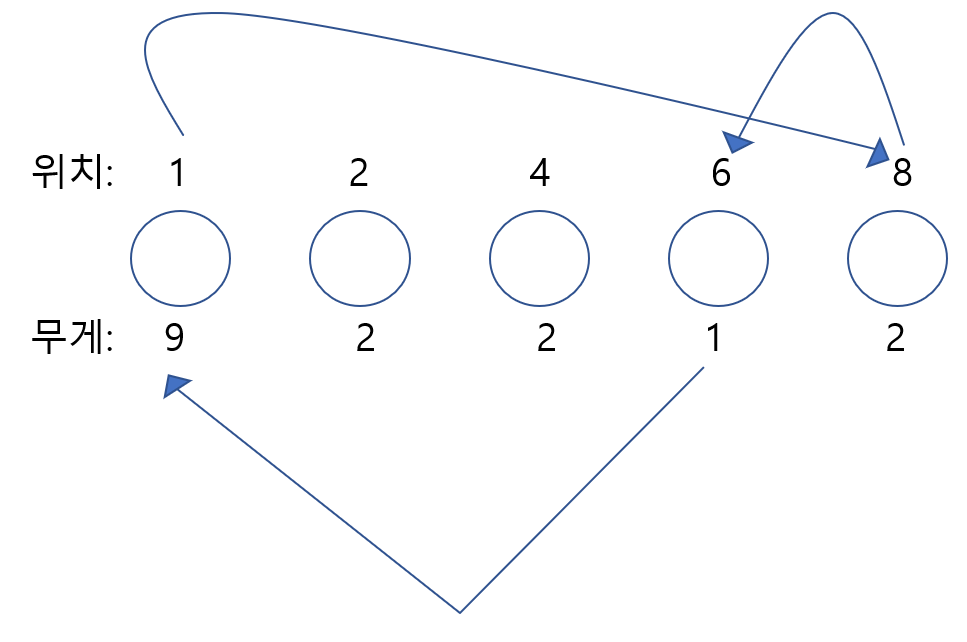
이를 알고리즘으로 나타내면 개미들을 무게 순으로 정렬한뒤, 같은 짐 무게의 개미들의 위치도 오름차순으로 정렬해준다. 그리고 각 개미들의 "(원래 위치) - (현재 위치)"의 절대값을 모두 더해주면 정답이다.
하지만 예외가 있었는지 에러 없이 100점 만점 중 20점을 획득했다.
코드)
public static void main(String[] args) throws Exception {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(bf.readLine());
for(int test_case = 0; test_case < T; test_case++) {
System.out.println("Case #"+(test_case+1));
//개미 수
int n = Integer.parseInt(bf.readLine());
//위치
int[][] m = new int[300000][2];
int[] loc = new int[300000];
String ant_loc = bf.readLine();
StringTokenizer st2 = new StringTokenizer(ant_loc);
//무게
for(int i = 0; i<n; i++) {
m[i][1] = Integer.parseInt(st2.nextToken());
loc[i] = m[i][1];
}
String ant_weight = bf.readLine();
StringTokenizer st3 = new StringTokenizer(ant_weight);
for(int i = 0; i<n; i++) {
m[i][0] = Integer.parseInt(st3.nextToken());
}
Arrays.sort(m, 0, n, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if(o1[0] == o2[0]) {
return o1[1] - o2[1];
}
else {
return o1[0] - o2[0];
}
}
});
int answer = 0;
for(int i = 0; i < n; i++) {
answer += Math.abs(m[i][1] - loc[i]);
}
System.out.println(answer);
}
}2번 K등분
n개의 일렬로 나열된 숫자를 k개의 그룹으로 묶고 (단, 그룹은 연속된 수들 끼리만 묶을 수 있다) 이 묶음 안의 숫자들의 합이 모두 같은 경우의 수를 구하는 문제였다.
입력) 첫 줄에 n값, k값 두번 째 줄에 n개의 숫자
출력) 조건을 만족하며 그룹으로 묶을 수 있는 경우의 수
예시 입력) 예시 출력)
6 3 3
3 0 3 0 3 0
풀이) 시간과 정신 모두 갉아먹었던 문제였다. 2번째 문제길레 뒤에서 2번째 난이도라 생각했지만 만점자는 3번째 문제보다 적었다. 이 문제를 쉽게 보면 N의 숫자를 K개의 숫자의 합으로 나타낸 뒤 각 K개의 그룹 안의 숫자들이 같은 값을 가지는지 확인하고 같다면 (경우의 수 + 1) 라고 볼 수 있다. 하지만 시간 초과 문제가 발생한다
그래서 내가 생각한 방안은 말로 표현하기 힘들어서 그림으로 설명하겠다.
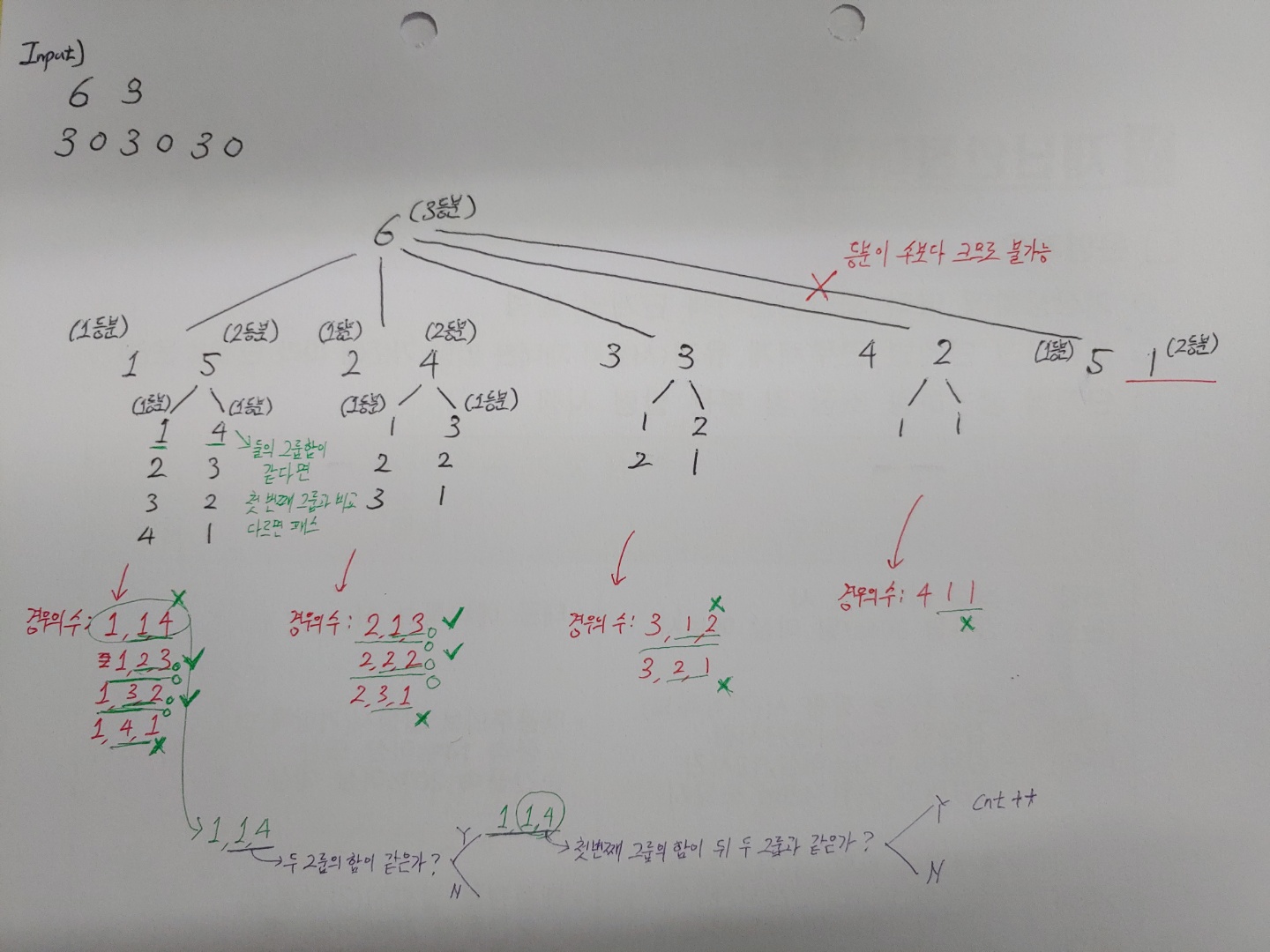
코드)
public static boolean div(int[] number, int s, int e, int d, ArrayList<Integer> value) {
System.out.println("Start: "+s+" End: "+e);
if(d == 1) {
int sum = 0;
for(int i = s; i<=e; i++) {
sum += number[i];
}
value.add(sum);
return true;
}
else {
int ns = s+1;
while(ns != e+1 && e-ns+1 >= d-1) {
ArrayList<Integer> leftValue = new ArrayList<>();
ArrayList<Integer> rightValue = new ArrayList<>();
boolean checkL = false;
boolean checkR = false;
checkL = div(number,s,ns-1,1,leftValue);
checkR = div(number,ns,e,d-1,rightValue);
if(checkL && checkR) {
for(Integer compL : leftValue) {
for(Integer compR : rightValue) {
if(compL == compR) {
value.add(compL);
}
}
}
}
if(d-1 == 1) {
//n개의 숫자를 m등분의 합으로 나타내는 경우의 수
System.out.println("C++");
call++;
}
ns += 1;
}
if(value.size() == 0) {
return false;
}
else {
return true;
}
}
}시간 지나고 다시 생각해보니 복잡한 재귀함수보다 N개의 숫자를 앞에서부터 묶고 합이 같을 때까지 추가하는 방법도 가능할 것 같고 훨씬 간결한 코드를 작성할 수 있을 것 같다.
(예를 들어 6을 3개의 합으로 나타낼 때, 처음 1개를 1그룹으로 한다면 2번째 부터 1개의 그룹과 합이 같을 때까지 묶고 나머지 묶었을 때 합 비교)
모임 후기 + SCPC 1차 예선 후기)
필자는 평소 Python으로 백준을 풀어서 이번 Python이 불가능한 SCPC에서 Java로 코테를 준비한건 첨이다. 이 때문에 안 좋은 성적을 낸건 핑계겠지만 다음 준비할 대회는 Java로도 원하는 코드를 마음껏 구현할 수 있도록 문법과 java만의 색깔에 익숙해지고자 한다.
참고로 대중적인 C++로 코테를 준비하지 않은 이유는 앞으로 프로젝트를 할 때 Java로 스프링 백엔드나 Kotlin같은 프레임워크들을 사용하기 위해 Java에 능숙해지고 싶기 때문이다.

