LSA(Latent Semantic Analysis), 잠재 의미 분석이란 기본적으로 단어의 빈도 수를 이용한 수치화 방법입니다. 이 알고리즘의 근원은 따지고 보면 NLP입니다. BoW에 기반한 DTM이나 TF-IDF는 기본적으로 단어의 빈도 수를 이용한 수치화 방법이기 때문에 단어의 의미를 고려하지 못한다는 단점이 있었고, 이를 위한 대안으로 LSA라는 방법이 나왔습니다.
미션은 SVD인데 왜 LSA 이야기를 하고 있냐구요? LSA를 이해하기 위해서는 SVD에 대해 잘 알아야 하기 때문입니다.
Latent (잠재된) 의미를 제대로 이끌어내기 위해서는, 나름대로의 <차원 축소 기술>이 필요합니다. 그리고 이때, Truncated SVD가 사용됩니다. 이를 사용함으로써 기존의 행렬에서는 드러나지 않았던 심층적인 의미를 확인할 수 있게 되죠.
여기서부터 문제입니다. [SVD와 Truncated SVD]의 개념을 공부하고, 두 개의 차이에 대해 서술하세요.
대체 어떤 방식으로 차원 축소가 된다는 것일까요?
'일부 벡터들을 삭제하는 것으로 데이터의 차원을 줄인다' 라는 말의 의미를 이해하는 것이 이 미션의 목적입니다.
특이값 분해를 알기 이전에 고윳값 분해를 알아두는 것이 좋습니다.
- 고윳값(eigen value), 고유벡터(eigen vector)
고유벡터(eigen vector)와 고윳값(eigen value)은 정방행렬(정사각 행렬)일때만 정의되고, 선형변환을 진행했을때 방향이 바뀌지 않고 크기만 변한것을 말하며, 이를 고유벡터(eigen vector), 고유값은 (선형변환 후 벡터 크기 / 선형변환 전 벡터 크기)만큼 입니다. 즉, 증가한 벡터 크기 비율만큼이 고유값입니다.
(방향도, 크기도 변하지 않을경우에도 고유벡터 이며, 고윳값은 1입니다.) - 고윳값 분해(eigen decomposition)
예를 들어 행렬 A의 고유값을 λi, 고유벡터를 vi, i = 1, 2,..., n이라고 합니다.
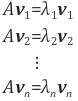
위 식을 한 번에 정리하면 아래와 같습니다.
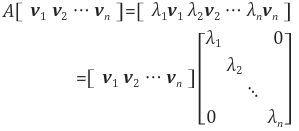
행렬 A의 고유 벡터들을 열 벡터로 하는 행렬을 V, 고유값을 대각원소로 가지는 대각 행렬을 Λ라 하면 다음 식이 성립합니다.
AV = VΛ
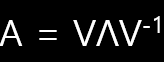
한 가지 특징을 언급하자면, 대칭 행렬은 모두 고유값 분해가 가능하며, 더군다나 직교 행렬로 분해할 수 있습니다. 이는 앞서 배워볼 특이값 분해를 이해하는데 필요하니 기억해두시면 좋습니다.
특이값 분해(Singular Value Decomposition, SVD)
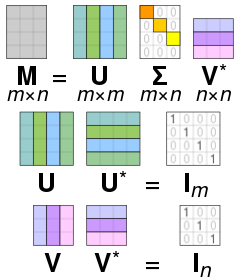
위에서 봤던 EVD는 정방행렬에서만 가능한것과는 다르게 SVD는 행과 열이 다른 직각행렬에서도 가능합니다.
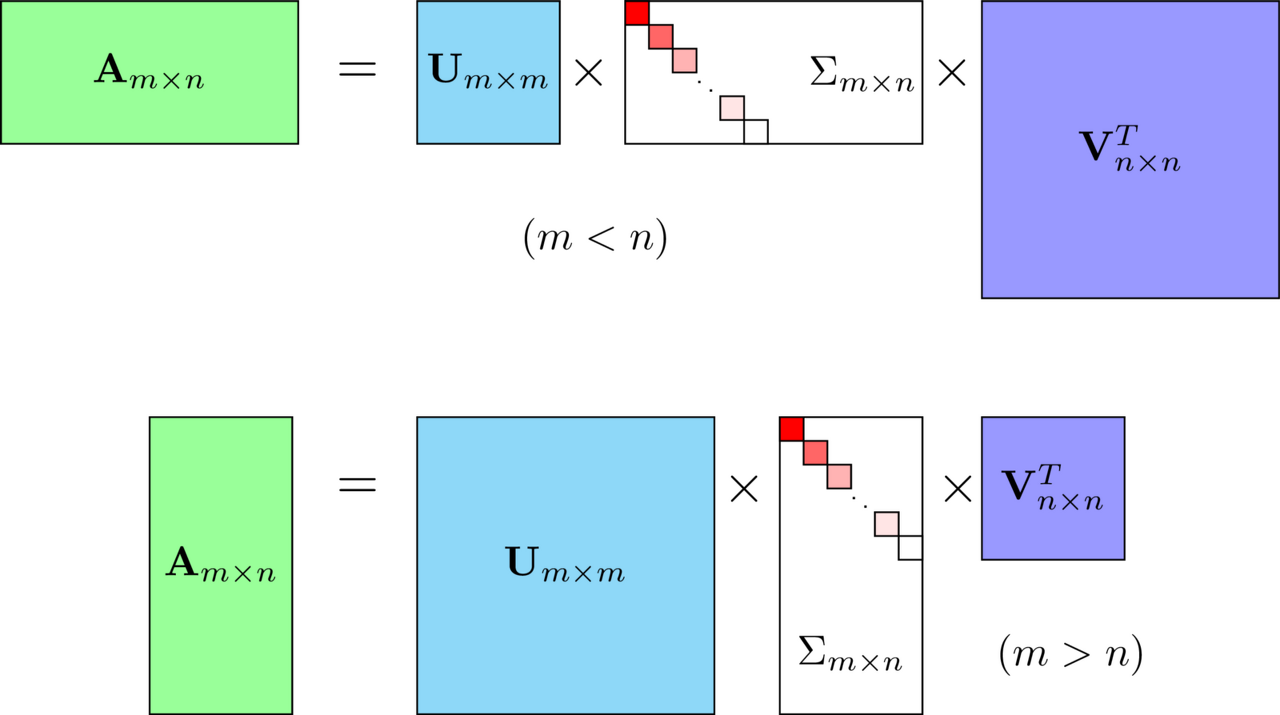
U와 V에 속한 모든 특이 벡터(Singular Vector)는 직교 행렬(orthogonal matrix)이며, ∑는 직사각 대각 행렬(diagonal matrix)로 대각의 위치한 숫자를 제외하고 전부 0입니다.
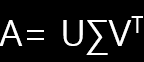
U는 Left Singular Value이며, Vt(Transpose)는 Right Singular Value라고 하며, ∑는 m x n의 직사각 대각 행렬입니다.
대각 행렬의 대각 성분은 At(Transpose)A 혹은 AAt(Transpose)의 고유값들에 루트를 씌워준 값으로 구성되어 있습니다.
대칭 행렬은 모두 고유값 분해가 가능하며, 더군다나 직교 행렬로 분해할 수 있습니다.SVD(Singular Value Decomposition)기아학적 의미
A = U ∑ Vt 에서 양변에 V를 내적해주면, A V = U ∑ 가 됩니다. U와 V에 속한 벡터는 서로 직교하는 성질을 가진다고 했습니다. 따라서 서로 직교하는 벡터로 구성된 행렬 V에 선형 변환 A를 해준 뒤에도 서로 직교하는 벡터로 구성된 행렬 U가 만들어집니다. 다만 그 크기가 ∑만큼 차이가 있습니다.
직교하는 벡터 집합 V에 대하여 선형 변환 A 후에도 그 크기는 ∑만큼 변하지만 여전히 직교하는 벡터 집합 U를 만듭니다.
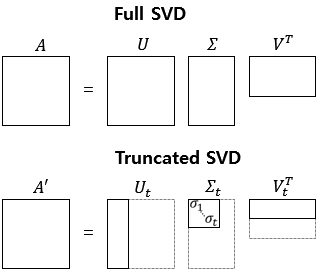
Full SVD와 Truncated SVD
위에서 설명한 SVD를 풀 SVD(Full SVD)라고 합니다.
일부 벡터들을 삭제시킨 잘린 SVD(Truncated SVD)는 대각 행렬 Σ의 대각 원소의 값 중에서 상위값 t개만 남게 됩니다.
잘린 SVD(Truncated SVD)를 수행하면 값의 손실이 일어나므로 Full SVD와 다르게 기존의 행렬 A를 복구할 수 없습니다.
또한, U행렬과 V행렬의 t열까지만 남깁니다. 여기서 t는 우리가 찾고자하는 토픽의 수를 반영한 Hyper-Paramater값입니다.
t를 선택하는 것은 쉽지 않은 일입니다. t를 크게 잡으면 기존의 행렬 A로부터 다양한 의미를 가져갈 수 있지만, t를 작게 잡아야만 노이즈를 제거할 수 있기 때문입니다.
이렇게 일부 벡터들을 삭제하는 것을 데이터의 차원을 줄인다고도 말하는데, 데이터의 차원을 줄이게되면 당연히 풀 SVD를 하였을 때보다 직관적으로 계산 비용이 낮아지는 효과를 얻을 수 있습니다.
하지만 계산 비용이 낮아지는 것 외에도 상대적으로 중요하지 않은 정보를 삭제하는 효과를 갖고 있는데, 이는 영상 처리 분야에서는 노이즈를 제거한다는 의미를 갖고, 자연어 처리 분야에서는 설명력이 낮은 정보를 삭제하고 설명력이 높은 정보를 남긴다는 의미를 갖고 있습니다. 즉, 다시 말하면 기존의 행렬에서는 드러나지 않았던 심층적인 의미를 확인할 수 있게 해줍니다.
[출처 : https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-19-%ED%96%89%EB%A0%AC]
[출처 : https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-20-%ED%8A%B9%EC%9D%B4%EA%B0%92-%EB%B6%84%ED%95%B4Singular-Value-Decomposition]
[출처 : https://wikidocs.net/24949]
