ch10. 최단경로

최단 경로 알고리즘: 가장 짧은 경로를 찾는 알고리즘

다양한 문제 상황

• 한 지점에서 다른 한 지점까지의 최단 경로
• 한 지점에서 다른 모든 지점까지의 최단 경로 → 다익스트라 알고리즘
• 모든 지점에서 다른 모든 지점까지의 최단 경로 → 플로이드 워셜 알고리즘

각 지점은 그래프에서 노드로 표현

지점 간 연결된 도로는 그래프에서 간선으로 표현

최단 경로 알고리즘 동작 과정

• 최단 거리 테이블은 각 노드에 대한 현재까지의 최단 거리 정보를 가짐
• 처리 과정에서 더 짧은 경로를 찾으면 더 짧은 경로로 값을 갱신

다익스트라 알고리즘

• 특정한 노드에서 출발하여 다른 모든 노드로 가는 최단 경로 계산
• 다익스트라 알고리즘은 음의 간선이 없을 때 정상적으로 동작
  • 현실 세계의 간선은 음의 간선으로 표현X
  • 음의 간선이 포함될 때는 벨만 포드 알고리즘 사용
• 그리디 알고리즘으로 분류됨 → 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정 반복

다익스트라 알고리즘 동작 과정

1. 출발 노드 설정

2. 최단 거리 테이블 초기화

3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드 선택

4. 해당 노드를 거쳐 다른 노드로 가는 비용 계산하여 최단 거리 테이블 갱신

   → 최단 거리 테이블을 직접 갱신하지 않고, 우선순위 큐에 삽입하는 방식 사용 가능

   우선순위 큐: 우선순위가 가장 높은 데이터를 가장 먼저 삭제하는 자료구조

   • 힙(최소 힙: 부모 노드는 항상 자식 노드보다 값이 작아야 함, 최대 힙: 부모 노드는 항상 자식 노드보다 크거나 같아야 함) 자료 구조 이용하여 구현
   • 시간 복잡도: O(logN)
   • JS에서는 우선순위 큐 라이브러리 제공X (필요한 경우 별도의 라이브러리 사용)

5. 위 과정에서 3번과 4번 반복

ex) 1번노드부터 각 노드까지의 최단 거리 비용 구하기

• 처리된 간선은 다시 방문하지 않음!

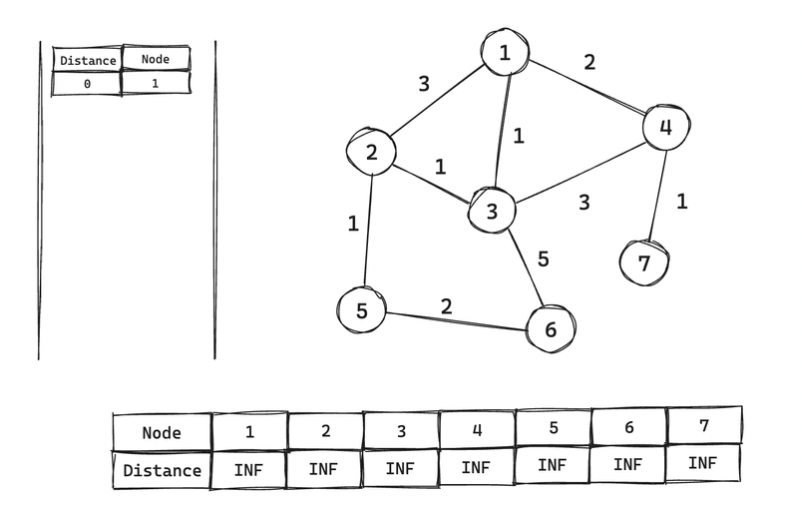
1. 출발 노드 설정 → 1번(자기 자신의 위치까지의 거리는 0임!)

   

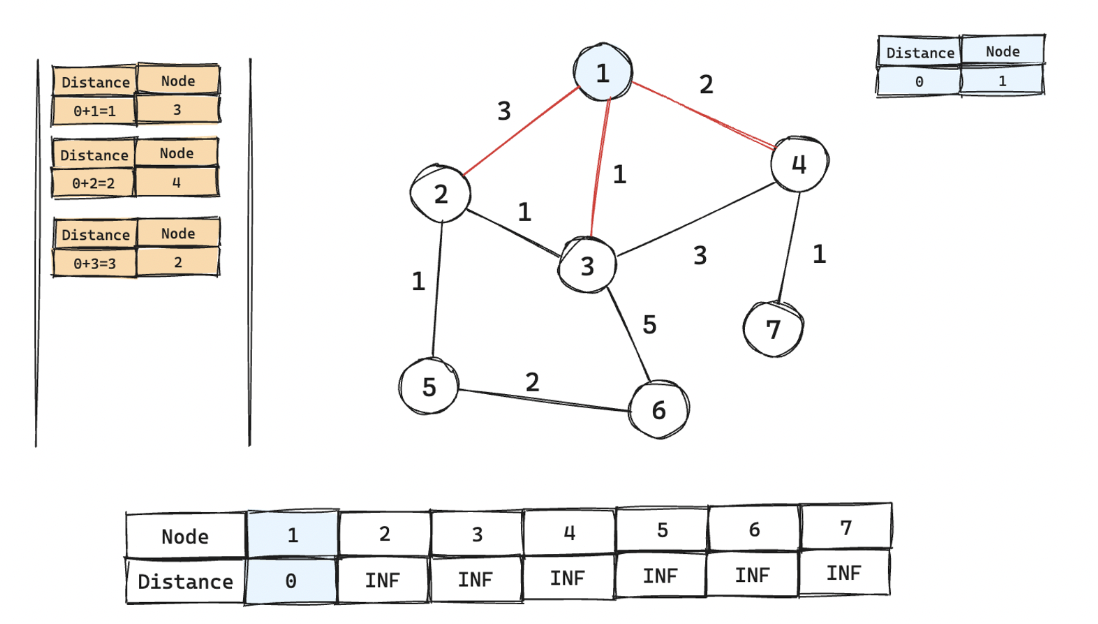
   • 따라서 가장 짧은 거리는 0!
   • 우선순위 큐에 연결된 노드 넣을 때 거리가 가장 짧은 것이 우선으로!

2. 3번 노드 꺼내어 거리 테이블 갱신 후, 연결된 간선들 우선순위 큐에 넣기

   

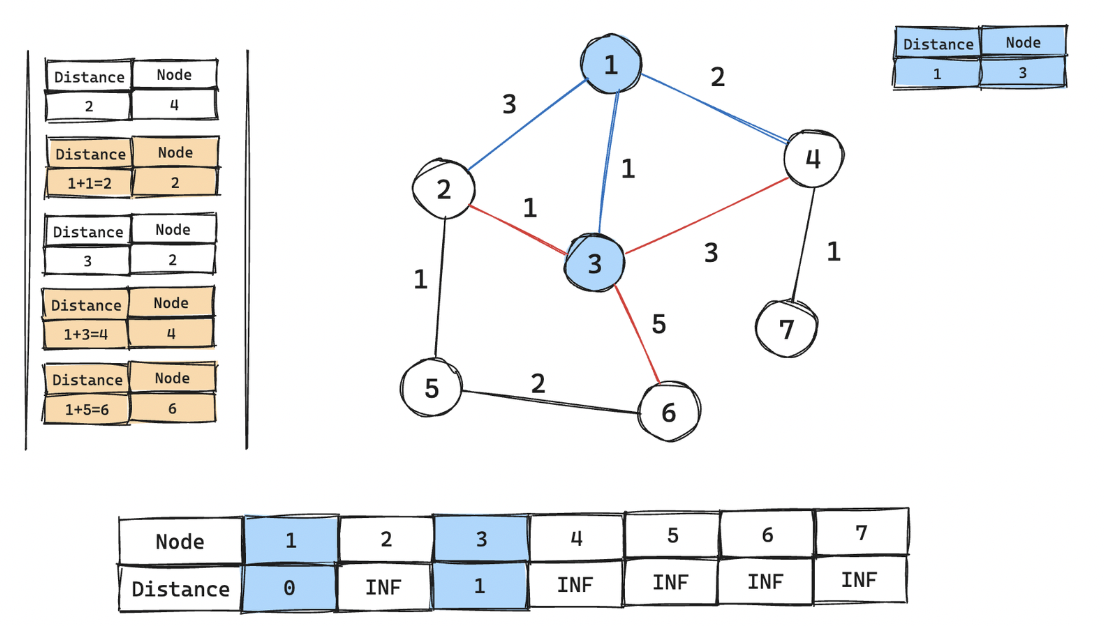
3. 4번 노드 꺼내어 거리 테이블 갱신 후, 연결된 간선 7 우선순위 큐에 넣기

   

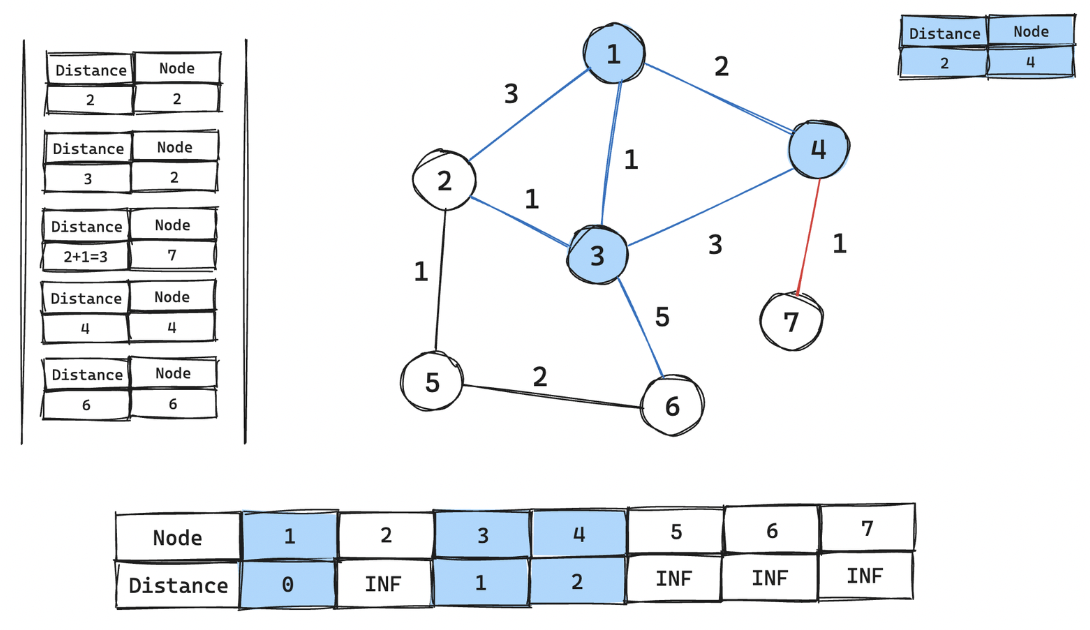
4. 2번 노드 꺼내어 거리 테이블 갱신 후, 연결된 간선 5 우선순위 큐에 넣기

   

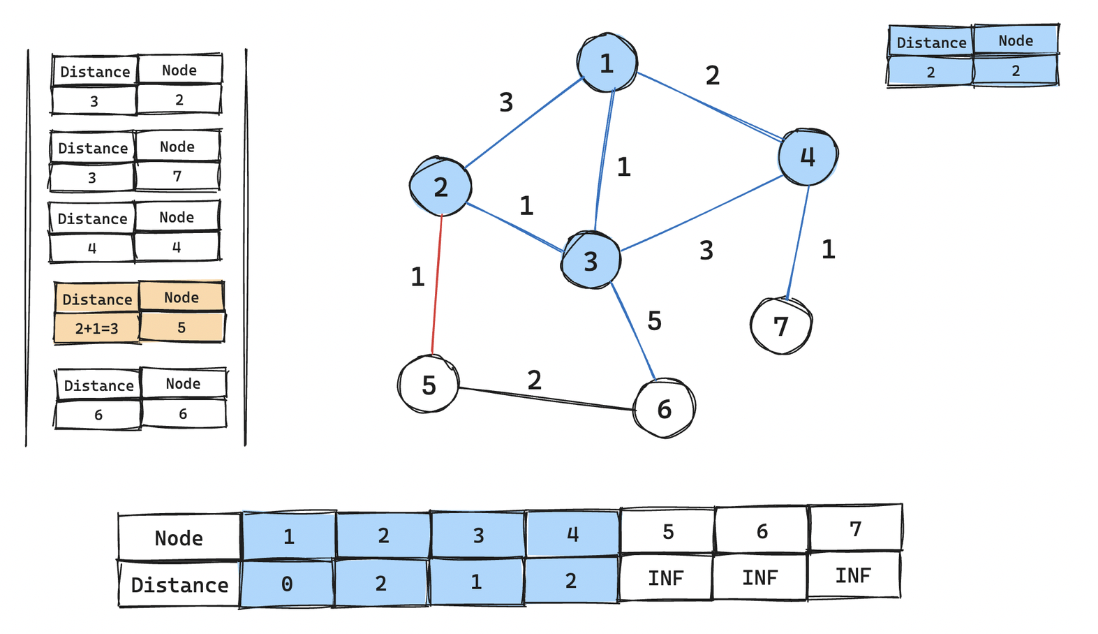
5. 거리 테이블의 2번이 현재 꺼내진 값보다 비용이 더 작으므로 그냥 꺼내기만하기

   

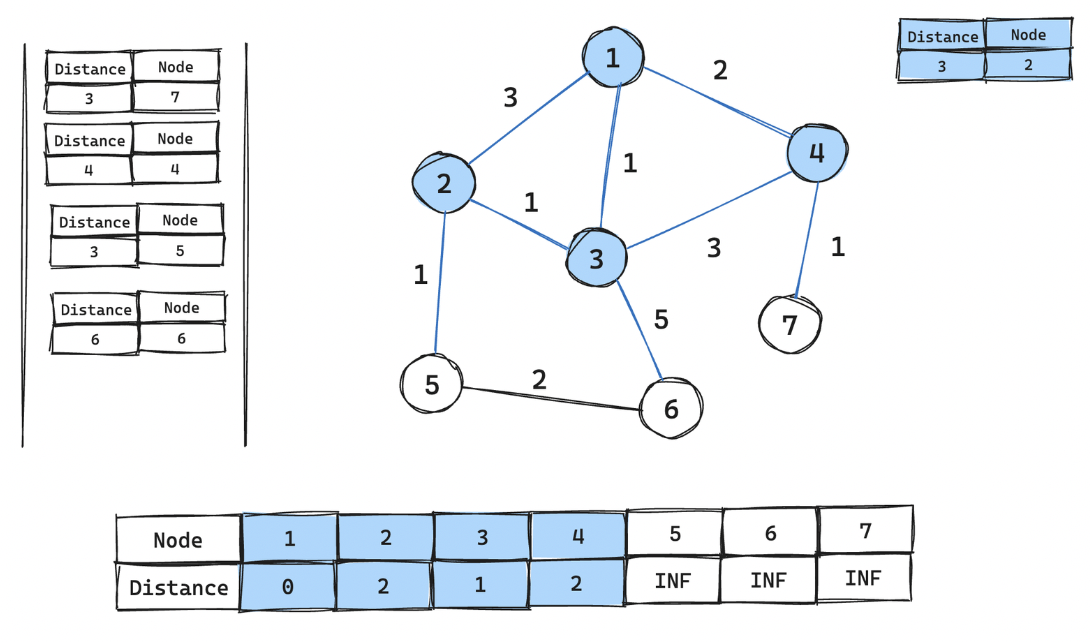
6. 7번 노드 꺼내어 거리 테이블 갱신 → 연결된 간선 없음

   

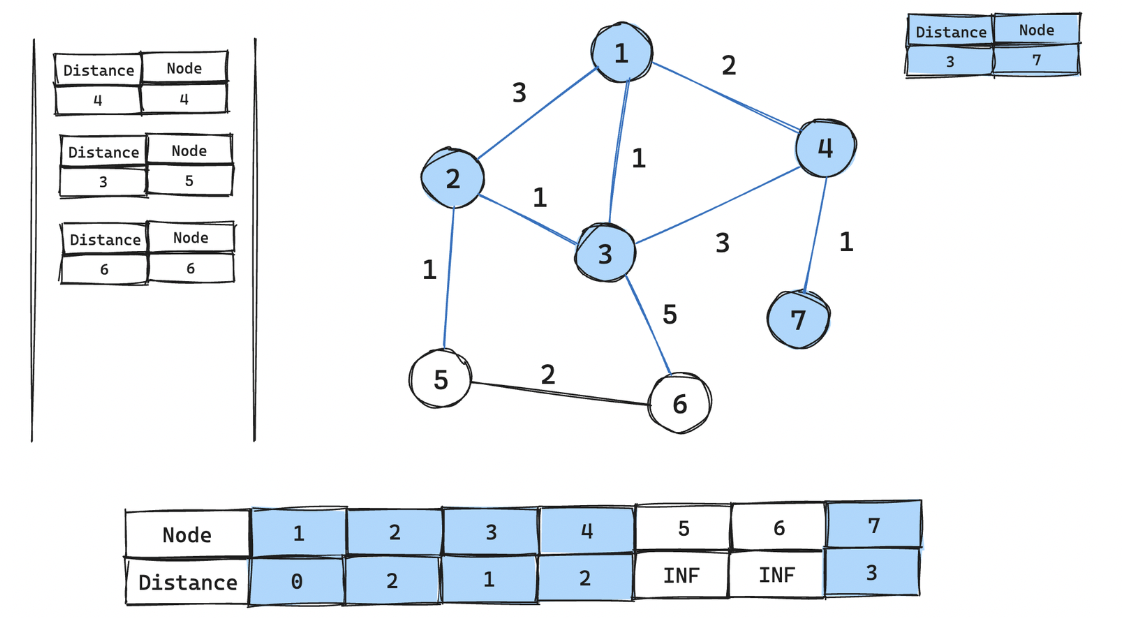
7. 4번 노드 역시 거리 테이블에 있는 값이 현재 꺼내지는 비용보다 작으므로 그냥 꺼내기만 하기

   

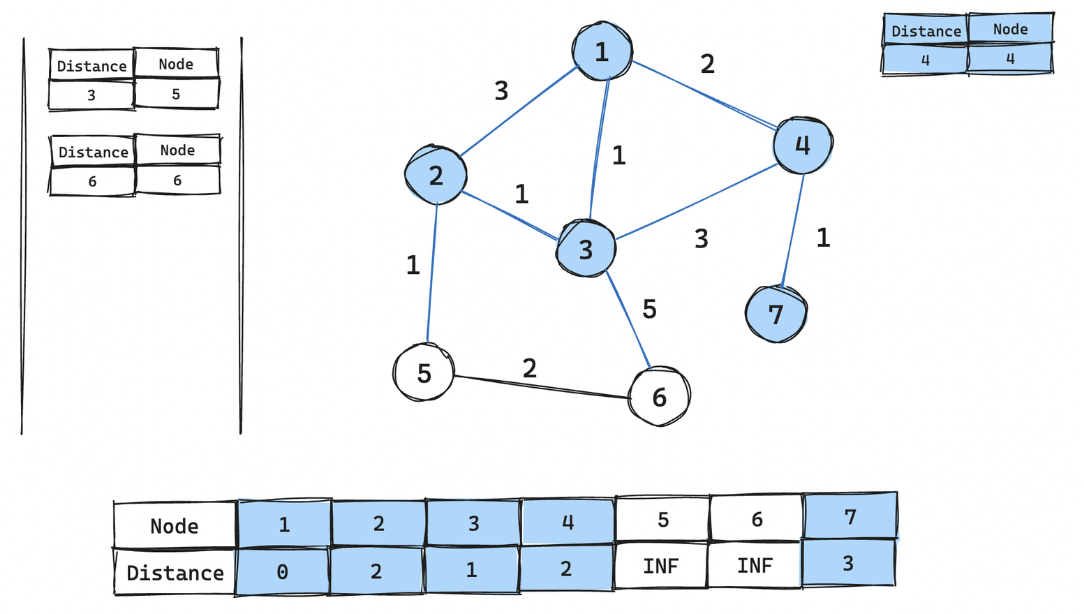
8. 5번 노드 꺼내어 거리 테이블 갱신 후, 연결된 6번 노드와 거리 비용을 우선순위 큐에 넣기

   

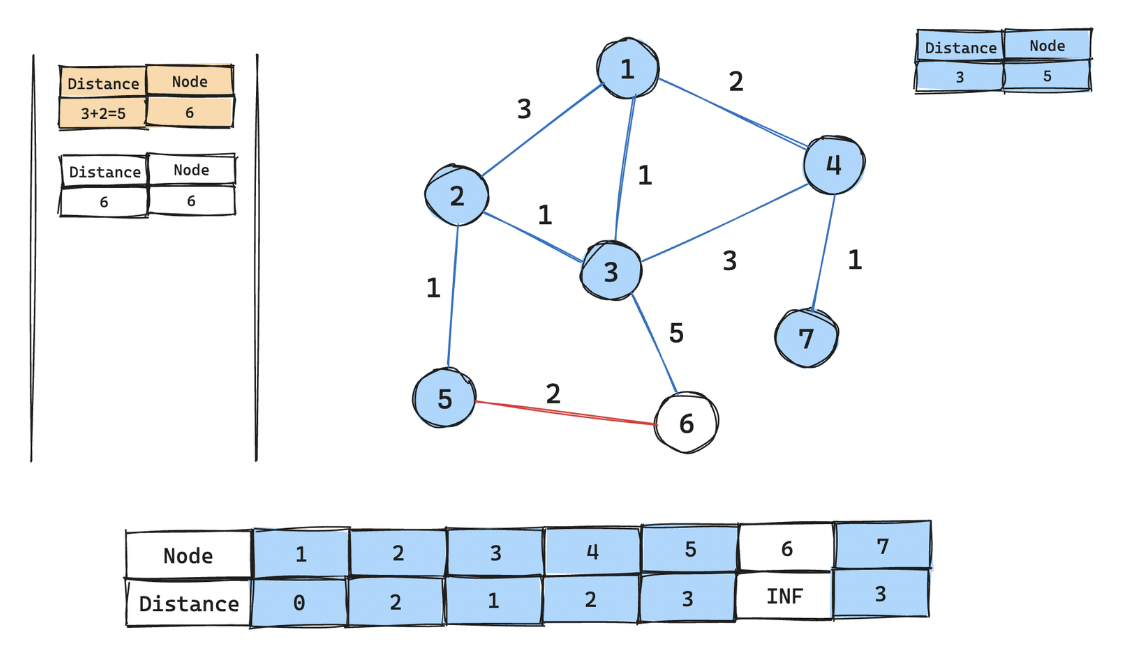
9. 6번 노드 꺼내어 거리 테이블 갱신

   

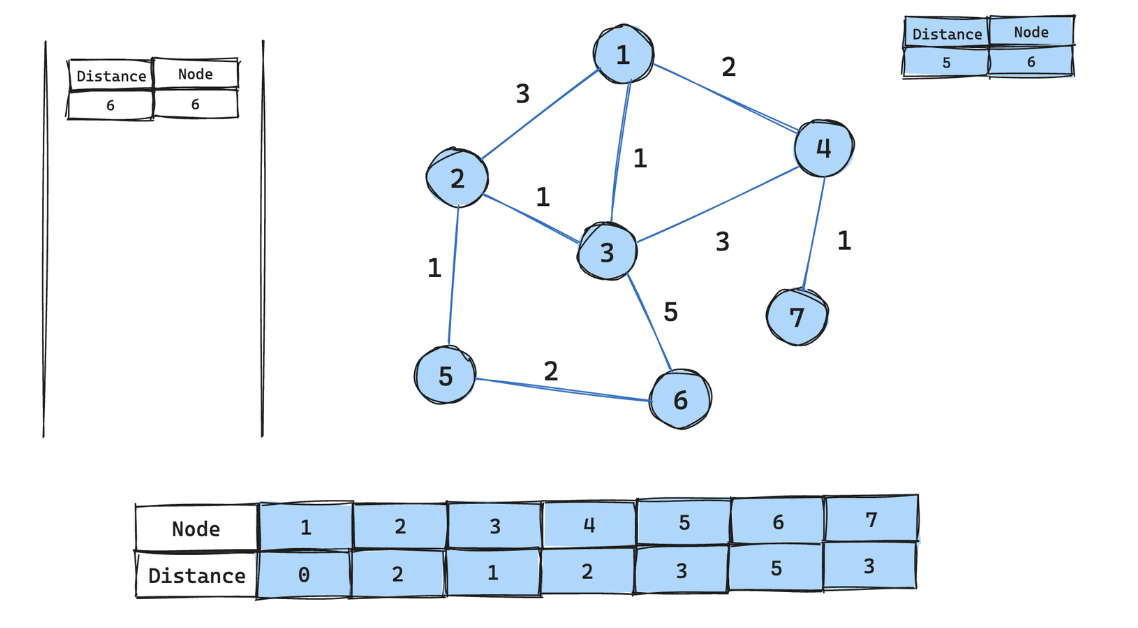
10. 우선순위 테이블에 남아있는 6번 노드의 비용이 현재 거리 테이블보다 더 크므로 그냥 꺼내기만 하기

    

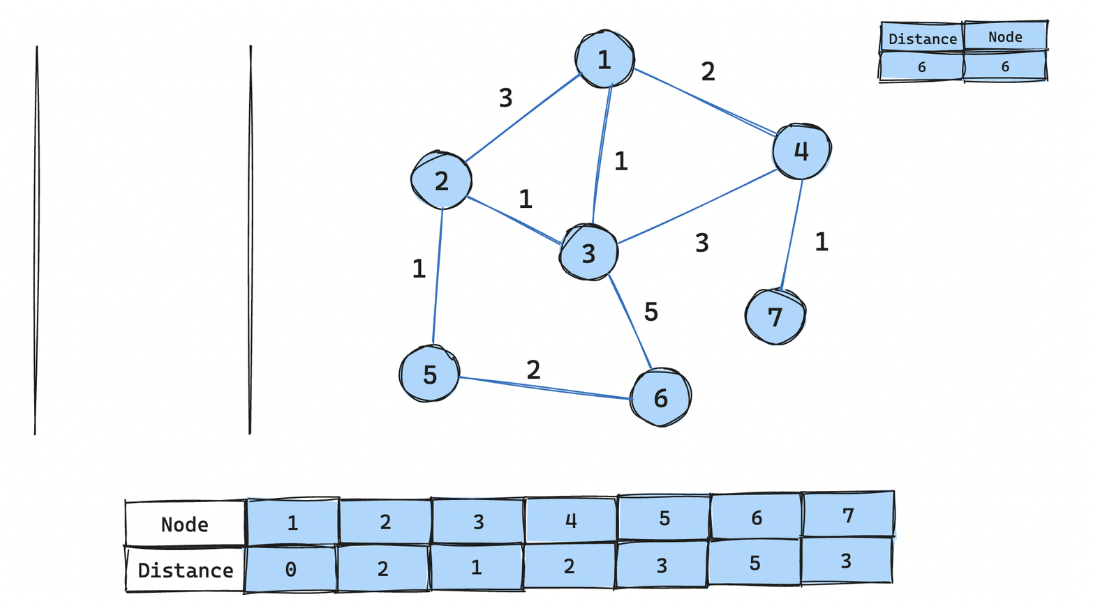
특징

• 단계를 거치며 한 번 처리된 노드의 최단 거리는 고정되어 더 이상 바뀌지 않음
  • 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해
• 다익스트라 알고리즘 수행한 뒤에 테이블에 각 노드까지의 최단 거리 정보가 저장됨
• 단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드 선택
  • 이를 위해 힙 자료구조 이용
  • 현재 상황에서 가장 가까운 노드를 저장해 놓기 위해서 힙 자료구조 이용
  • 현재의 최단 거리가 가장 짧은 노드를 선택해야 하므로 최소 힙 사용

소스코드 예시

다익스트라 알고리즘

// 다익스트라 알고리즘 수행
function dijkstra() {
  let pq = new PriorityQueue((a, b) => b[0] - a[0]); // 최소힙
  // 시작 노드로 가기 위한 최단 거리는 0으로 우선순위 큐에 삽입
  pq.enq([0, start]);
  distance[start] = 0;
  // 우선순위 큐가 비어있지 않다면(우선순위 큐가 빌 때까지 반복)
  while (pq.size() != 0) {
    // 가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
    let [dist, now] = pq.deq();
    // 현재 노드가 이미 처리된 적이 있는 노드라면 무시
    if (distance[now] < dist) continue;
    // 현재 노드와 연결된 다른 인접한 노드들을 확인
    for (let i of graph[now]) {
      let cost = dist + i[1];
      // 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
      if (cost < distance[i[0]]) {
        distance[i[0]] = cost;
        pq.enq([cost, i[0]]);
      }
    }
  }
}

위의 예제 소스코드

let INF = 1e9; // 무한을 의미하는 값으로 10억 설정
let n = 7; // 노드의 개수
let start = 1;
// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트
// 각 간선은 [노드, 비용] 형태
let graph = [
  [],
  [
    [2, 3],
    [3, 1],
    [4, 2],
  ],
  [
    [1, 3],
    [3, 1],
    [5, 1],
  ],
  [
    [1, 1],
    [2, 1],
    [4, 3],
    [6, 5],
  ],
  [
    [1, 2],
    [3, 3],
    [7, 1],
  ],
  [
    [2, 1],
    [6, 2],
  ],
  [
    [3, 5],
    [5, 2],
  ],
  [[4, 1]],
];
// 최단 거리 테이블 모두 무한으로 초기화
let distance = new Array(n + 1).fill(INF);

// 다익스트라 알고리즘 수행
dijkstra();
// 모든 노드로 가기 위한 최단 거리 출력
for (let i = 1; i <= n; i++) {
  // 도달할 수 없는 경우 무한(INFINITY)으로 출력
  if (distance[i] == INF) console.log("INFINITY");
  else console.log(distance[i]);
}

다익스트라 알고리즘의 시간 복잡도

• 힙 자료 구조 이용 → O(ElogV)
  • 노드 하나씩 꺼내 검사하는 반복문은 노드의 개수 V이상의 횟수로 처리 X
  • E개의 원소를 우선순위 큐에 넣었다가 모두 빼내는 연산과 매우 유사