백트래킹 알고리즘

Ch06. 백트래킹 알고리즘

• 모든 경우의 수 고려할 때 사용
• 일반적으로 그래프/트리의 모든 원소를 완전 탐색하기 위한 목적으로 사용

DFS와의 차이점

• DFS: 일반적으로 완전 탐색 목적으로, 재귀 함수를 이용해 구현
• 백트래킹: 재귀 함수 이용하여 구현하는 것이 일반적이지만, 단순히 완전 탐색하는 것이 아니라 조건에 따라서 유망한 노드로 이동!

그래프 표현 방식(2가지)

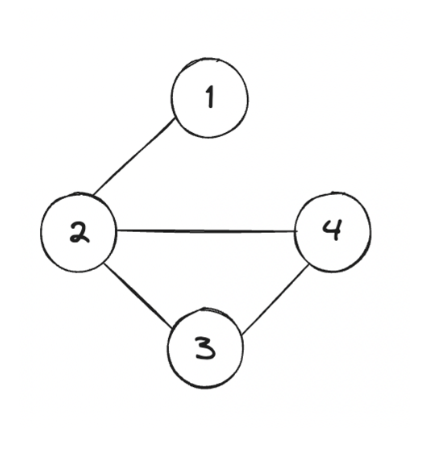
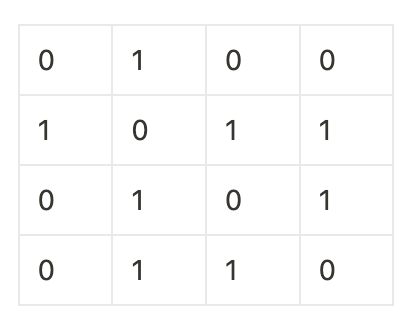
인접 행렬

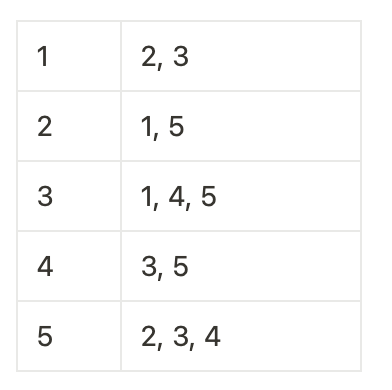
인접 리스트

N-Queen 문제

문제: NXN 체스 보드 위에 퀸 N개가 서로 공격할 수 없게 놓는 문제

풀이

• 64개의 위치에 8개의 퀸을 설치하는 모든 조합의 수는 Combination(64,8)
  → 각 퀸이 서로 공격 가능한지 검사하는 방식 사용하면 경우의 수가 매우 커짐
  
• 따라서, 완전 탐색을 하더라도 유망한 경우에서만 탐색 가능하도록하기
  1. N개의 퀸을 놓기 위해서는 각 행마다 1개씩의 퀸을 놓아야 함 → $2^{24}$
  2. 트리 혹은 그래프 구조로 표현하여 다른 퀸을 놓을 위치 고려 → 이전까지 놓았던 퀸들과 상충되지 않는 조건을 만족하는 위치에 대해서만 재귀 함수 호출

let n = 0; // 전체 맵(map)의 크기
let queens = []; // 현재 체스판에 놓은 퀸의 위치 정보들

// (x, y) 위치에 퀸을 놓을 수 있는지 확인
function possible(x, y) {
  // 현재까지 놓았던 모든 퀸의 위치를 하나씩 확인하며
  for (let [a, b] of queens) {
    if (a == x || b == y) return false; // 행이나 열이 같다면 놓을 수 없음
    if (Math.abs(a - x) == Math.abs(b - y)) return false; // 대각선에 위치한 경우 놓을 수 없음
  }
  return true;
}

let cnt = 0;
function dfs(row) {
  if (row == n) cnt += 1; // 퀸을 N개 배치할 수 있는 경우 카운트
  // 현재 행에 존재하는 열을 하나씩 확인하며
  for (let i = 0; i < n; i++) {
    if (!possible(row, i)) continue; // 현재 위치에 놓을 수 없다면 무시
    queens.push([row, i]); // 현재 위치에 퀸 놓기
    dfs(row + 1); // 재귀 함수 호출
    queens.pop(); // 혀냊 위치에서 퀸 제거
  }
}

⭐️ 백트래킹 기본 형태 ⭐️

function recursive() {
	if 종료 조건을 만족한다면 {
		처리;
	}
	for 자식 노드를 하나씩 확인하며 {
		if 임의의 조건을 만족한다면 {
			자식 노드 방문 처리;
			재귀 함수 호출;
			자식 노드 방문 처리 해제;
		}
	}
}