문제
n × n의 크기의 대나무 숲이 있다. 욕심쟁이 판다는 어떤 지역에서 대나무를 먹기 시작한다. 그리고 그 곳의 대나무를 다 먹어 치우면 상, 하, 좌, 우 중 한 곳으로 이동을 한다. 그리고 또 그곳에서 대나무를 먹는다. 그런데 단 조건이 있다. 이 판다는 매우 욕심이 많아서 대나무를 먹고 자리를 옮기면 그 옮긴 지역에 그 전 지역보다 대나무가 많이 있어야 한다.
이 판다의 사육사는 이런 판다를 대나무 숲에 풀어 놓아야 하는데, 어떤 지점에 처음에 풀어 놓아야 하고, 어떤 곳으로 이동을 시켜야 판다가 최대한 많은 칸을 방문할 수 있는지 고민에 빠져 있다. 우리의 임무는 이 사육사를 도와주는 것이다. n × n 크기의 대나무 숲이 주어져 있을 때, 이 판다가 최대한 많은 칸을 이동하려면 어떤 경로를 통하여 움직여야 하는지 구하여라.
입력
첫째 줄에 대나무 숲의 크기 n(1 ≤ n ≤ 500)이 주어진다. 그리고 둘째 줄부터 n+1번째 줄까지 대나무 숲의 정보가 주어진다. 대나무 숲의 정보는 공백을 사이로 두고 각 지역의 대나무의 양이 정수 값으로 주어진다. 대나무의 양은 1,000,000보다 작거나 같은 자연수이다.
출력
첫째 줄에는 판다가 이동할 수 있는 칸의 수의 최댓값을 출력한다.
예제 입력 1
4
14 9 12 10
1 11 5 4
7 15 2 13
6 3 16 8예제 출력 1
4풀이 및 해설(시간초과발생)
출력값: 판다가 이동할 수 있는 칸의 최댓값
상하좌우로 이동 가능할 때, 다음 칸에 있는 대나무 > 현재 칸에 있는 대나무
- 각 칸에서 시작했을 때, 이동할 수 있는 최댓값 갱신하기 → DFS 이용
- 상하좌우로 이동할 때, 대나무 숲의 범위를 벗어나지 않으면서 다음 칸의 대나무가 현재 칸의 대나무보다 많을 경우에만 다음 칸으로 이동
Code
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const n = +input[0]; // 대나무 숲의 크기
const forest = [];
for (let i = 1; i <= n; i++) forest.push(input[i].split(' ').map(Number));
const drdc = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
const visited = Array.from({ length: n }, () => new Array(n).fill(false));
let result = Number.MIN_SAFE_INTEGER;
const dfs = (r, c, move) => {
for (const [dr, dc] of drdc) {
const [nr, nc] = [r + dr, c + dc];
if (nr < 0 || nr >= n || nc < 0 || nc >= n) continue;
if (forest[r][c] < forest[nr][nc]) {
visited[nr][nc] = true;
dfs(nr, nc, move + 1);
visited[nr][nc] = false;
} else result = Math.max(result, move);
}
};
for (let r = 0; r < n; r++) {
for (let c = 0; c < n; c++) {
visited[r][c] = true;
dfs(r, c, 1);
visited[r][c] = false;
}
}
console.log(result);모든 칸을 dfs 수행 →
각 DFS의 수행(메모이제이션이 없어서 이미 방문했던 곳 또 확인) →
따라서, 최악의 시간복잡도
시간초과 해결하기
해당 문제는 이미 방문한 곳은 또 확인하지 않기 위해 DP도 같이 이용
DP = 각 칸에서 출발했을 때 이동할 수 있는 칸의 최대 수
1. 각 칸에서 시작했을 때의 DFS 수행
2. 이때, 이미 방문한 칸은 DFS를 수행하지 않고, 바로 해당 칸의 DP 값 리턴
3. 아직 방문하지 않은 경우, 해당 DP 값 1로 설정
4. 상하좌우로 이동가능하면서, 현재 대나무 < 다음 칸 대나무 조건을 만족하는 경우만 DFS 수행 → 이때, DFS 수행한 값 중 가장 큰 값으로 현재 DP값 설정
그림으로 설명
-
14에서 출발
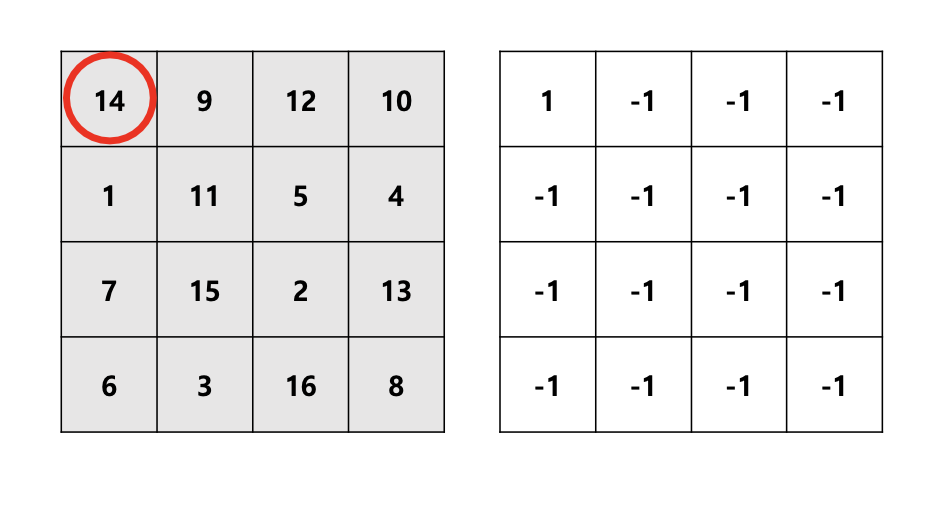
14의 경우 이동할 수 있는 칸의 수가 본인 하나임(DP 1로 설정)
-
9에서 출발(아직 방문 X)
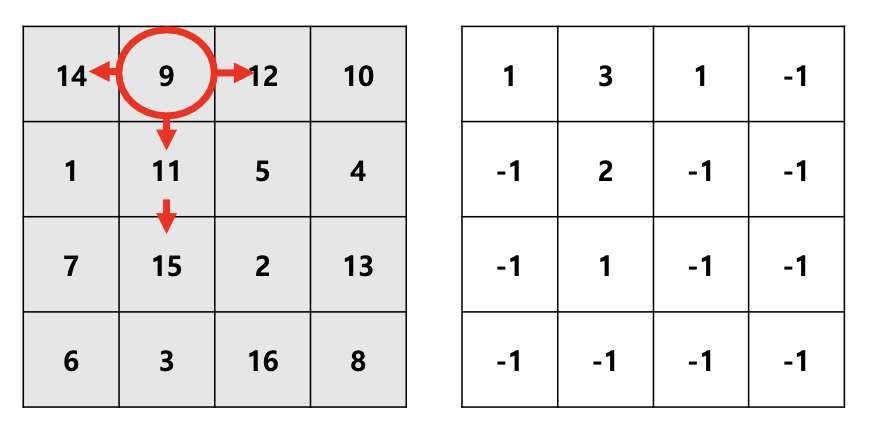
9의 경우 이동할 수 있는 경우가 좌(14), 우(12), 하(11)임- 좌로 이동(14)의 경우 이미 DP값 존재하므로 DP[0][0]+1 리턴
- 우로 이동(12)의 경우 DP[0][2]=1로 만든 후, DP[0][2]+1 리턴
- 하로 이동(11)의 경우 15로도 이동 가능하므로 DP[2][1]=1로 만든 후, DP[1][1]=2, DP[1][1]+1 리턴
따라서, DP[0][1] = Max(2, 2, 3) = 3
-
위와 같이 아직 방문하지 않은 경우 DP 값 설정
const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');
const n = +input[0]; // 대나무 숲의 크기
const forest = [];
for (let i = 1; i <= n; i++) forest.push(input[i].split(' ').map(Number));
const drdc = [
[-1, 0],
[1, 0],
[0, -1],
[0, 1],
];
const dp = Array.from({ length: n }, () => new Array(n).fill(-1)); // 현재 위치에서 이동할 수 있는 최대 칸의 수
let result = 1;
const dfs = (r, c) => {
// 아직 방문하지 않은 지점만 수행
if (dp[r][c] === -1) {
dp[r][c] = 0;
// 상하좌우 이동
for (const [dr, dc] of drdc) {
const [nr, nc] = [r + dr, c + dc];
if (nr < 0 || nr >= n || nc < 0 || nc >= n) continue;
if (forest[r][c] < forest[nr][nc]) {
dp[r][c] = Math.max(dp[r][c], dfs(nr, nc)); // 현재 위치에서 이동할 수 있는 거리 갱신
}
}
}
return dp[r][c] + 1;
};
// 각 칸 DFS 수행
for (let r = 0; r < n; r++) {
for (let c = 0; c < n; c++) {
result = Math.max(result, dfs(r, c));
}
}
console.log(result);