문제
어떤 동물원에 가로로 두칸 세로로 N칸인 아래와 같은 우리가 있다.
이 동물원에는 사자들이 살고 있는데 사자들을 우리에 가둘 때, 가로로도 세로로도 붙어 있게 배치할 수는 없다. 이 동물원 조련사는 사자들의 배치 문제 때문에 골머리를 앓고 있다.
동물원 조련사의 머리가 아프지 않도록 우리가 2*N 배열에 사자를 배치하는 경우의 수가 몇 가지인지를 알아내는 프로그램을 작성해 주도록 하자. 사자를 한 마리도 배치하지 않는 경우도 하나의 경우의 수로 친다고 가정한다.
입력
첫째 줄에 우리의 크기 N(1≤N≤100,000)이 주어진다.
출력
첫째 줄에 사자를 배치하는 경우의 수를 9901로 나눈 나머지를 출력하여라.
예제 입력 1
4예제 출력 1
41풀이 및 해설
출력값: N*2 배열에 사자를 배치하는 경우의 수(한 마리도 배치하지 않는 경우도 하나의 경우의 수임)
- 사자들은 가로든 세로든 붙어있으면 안됨!
1. N=1인 경우
-
사자를 배치하지 않음 ▶ 1가지
-
왼쪽 칸에 사자 1마리 배치 ▶ 1가지
-
오른쪽 칸에 사자 1마리 배치 ▶ 1가지
2. N=2인 경우
-
맨 윗줄에 사자를 배치하지 않음 ▶ 3가지
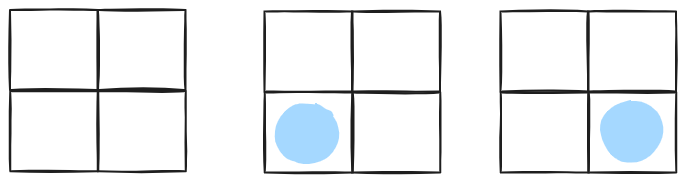
-
맨 윗줄 왼쪽에 사자 배치 ▶ 2가지
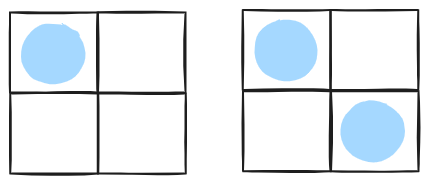
-
맨 윗줄 오른쪽에 사자 배치 ▶ 2가지
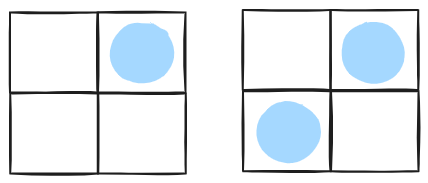
3. N=3인 경우
-
맨 윗줄에 사자를 배치하지 않음 ▶ 7가지
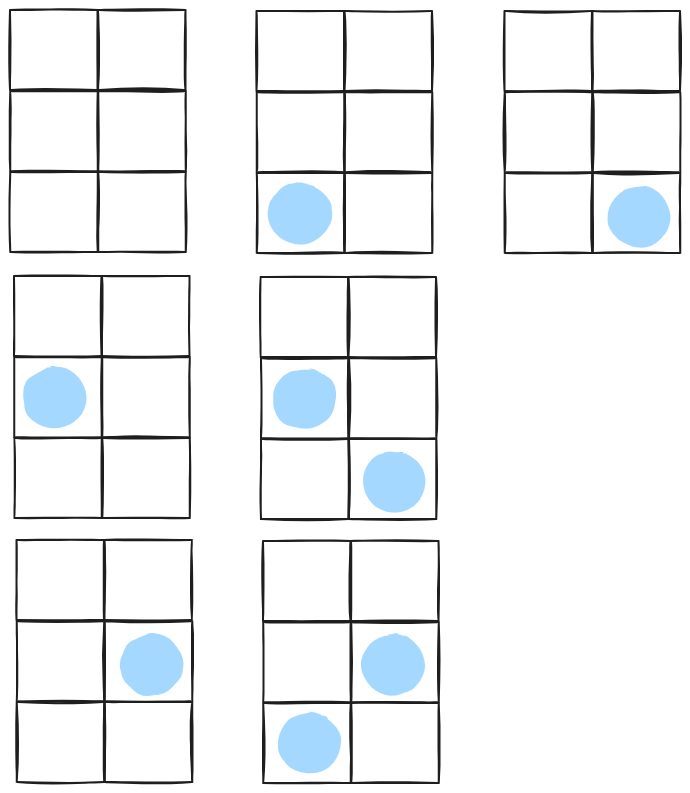
-
맨 윗줄 왼쪽에 사자 배치 ▶ 5가지
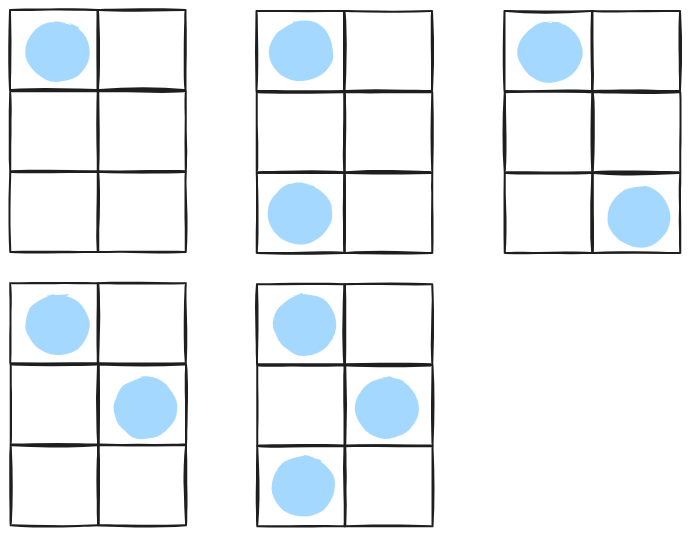
-
맨 윗줄 오른쪽에 사자 배치 ▶ 5가지
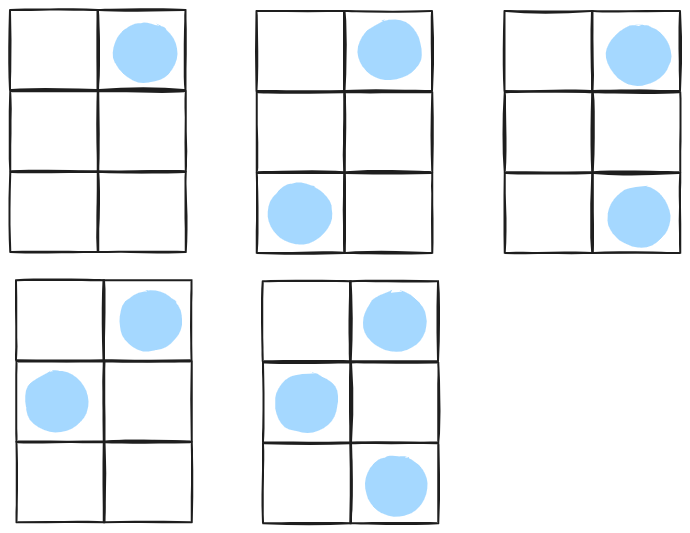
※ 위 규칙을 분석하면,
DP[i][j]: N=i일 때, 3가지 경우(0이 사자 배치X, 1이 왼쪽에 배치, 2가 오른쪽에 배치)
- 맨 윗줄에 사자를 배치하지 않는 경우 → DP[i][0] = DP[i-1][0]+DP[i-1][1] + DP[i-1][2]
- 맨 윗줄 왼쪽에 사자 배치하는 경우 → DP[i][1] = DP[i-1][0]+DP[i-1][2]
- 맨 윗줄 오른쪽에 사자 배치하는 경우 → DP[i][2] = DP[i-1][0]+DP[i-1][1]
Code
const fs = require("fs");
const input = fs.readFileSync("/dev/stdin").toString().split("\n");
const N = +input[0]; // 사자 우리의 크기
const dp = Array.from({ length: N }, () => new Array(3).fill(0));
// N=1일 때, 사자 배치 경우의 수 초기화
dp[0][0] = 1; // 사자를 놓지 않을 때
dp[0][1] = 1; // 사자를 왼쪽에 배치했을 때
dp[0][2] = 1; // 사자를 오른쪽에 배치했을 때
for (let i = 1; i < N; i++) {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2]) % 9901;
dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % 9901;
dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % 9901;
}
const total = dp[N - 1][0] + dp[N - 1][1] + dp[N - 1][2];
console.log(total % 9901);