백준_11049_행렬 곱셈 순서

행렬 곱셈 순서

문제

크기가 N×M인 행렬 A와 M×K인 B를 곱할 때 필요한 곱셈 연산의 수는 총 N×M×K번이다. 행렬 N개를 곱하는데 필요한 곱셈 연산의 수는 행렬을 곱하는 순서에 따라 달라지게 된다.

예를 들어, A의 크기가 5×3이고, B의 크기가 3×2, C의 크기가 2×6인 경우에 행렬의 곱 ABC를 구하는 경우를 생각해보자.

AB를 먼저 곱하고 C를 곱하는 경우 (AB)C에 필요한 곱셈 연산의 수는 5×3×2 + 5×2×6 = 30 + 60 = 90번이다.
BC를 먼저 곱하고 A를 곱하는 경우 A(BC)에 필요한 곱셈 연산의 수는 3×2×6 + 5×3×6 = 36 + 90 = 126번이다.
같은 곱셈이지만, 곱셈을 하는 순서에 따라서 곱셈 연산의 수가 달라진다.

행렬 N개의 크기가 주어졌을 때, 모든 행렬을 곱하는데 필요한 곱셈 연산 횟수의 최솟값을 구하는 프로그램을 작성하시오. 입력으로 주어진 행렬의 순서를 바꾸면 안 된다.

입력

첫째 줄에 행렬의 개수 N(1 ≤ N ≤ 500)이 주어진다.
둘째 줄부터 N개 줄에는 행렬의 크기 r과 c가 주어진다. (1 ≤ r, c ≤ 500)
항상 순서대로 곱셈을 할 수 있는 크기만 입력으로 주어진다.

출력

첫째 줄에 입력으로 주어진 행렬을 곱하는데 필요한 곱셈 연산의 최솟값을 출력한다. 정답은 231-1 보다 작거나 같은 자연수이다. 또한, 최악의 순서로 연산해도 연산 횟수가 231-1보다 작거나 같다.

예제 입력 1

3
5 3
3 2
2 6

예제 출력 1

90

풀이 및 해설

출력값: 행렬 N개를 곱할 때 필요한 곱셈 연산 횟수의 최솟값

ex) A: 5X4, B: 4X3, C: 3X2, D: 2X1
[ABCD 곱셈 구하는 방법]
→ ((AB)C)D) / ((AB)(CD)) / ((A(BC))D) / (A((BC)D)) / A(B(CD))
겹치는 부분 발생! ▶︎ DP 이용

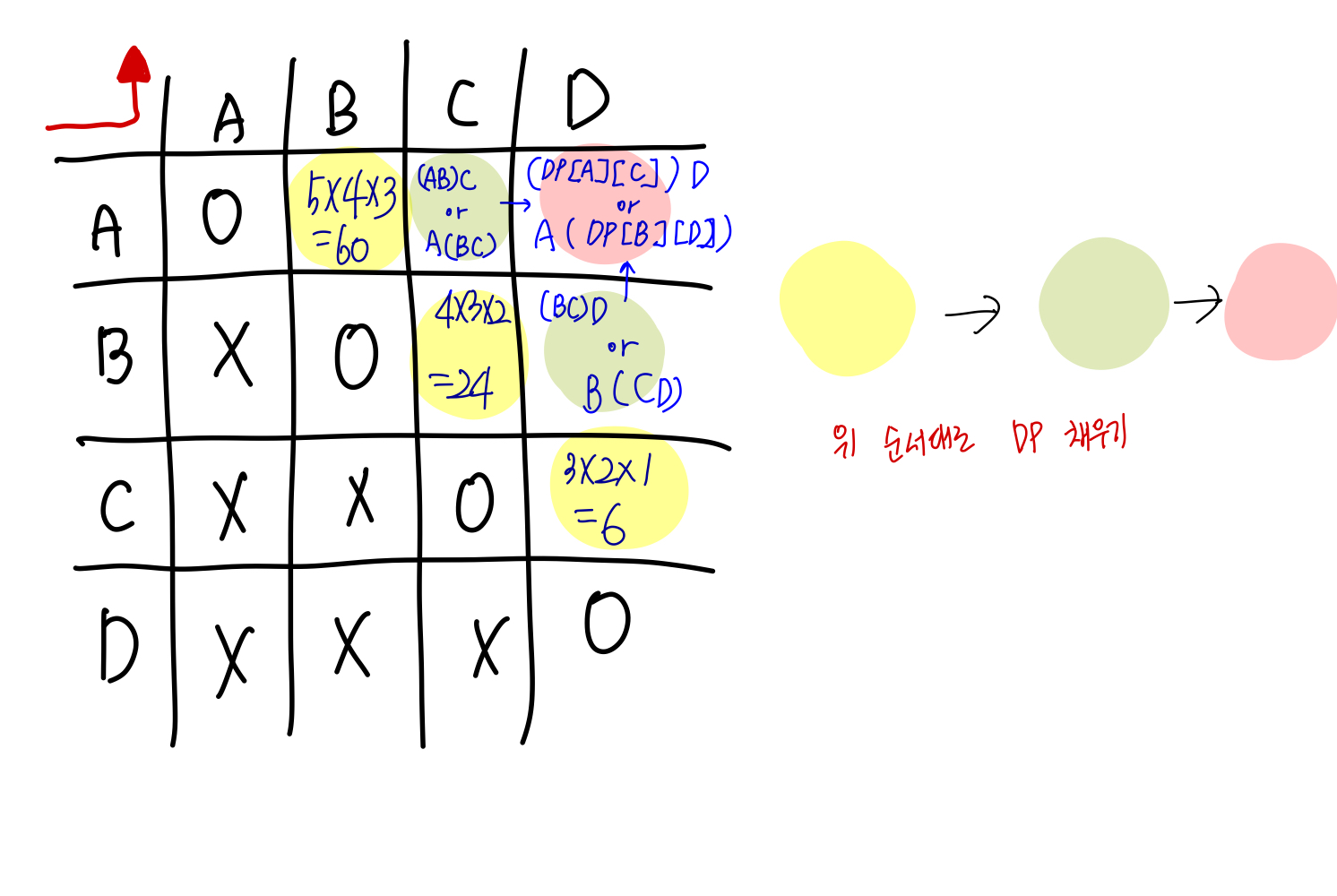
DP[A][C] = DP[A][B](5X3)+(M[A][0]*M[B][1]*M[C][1]) or DP[B][C](4X2)+(M[A][0]*M[B][0]*M[C][1])

DP[r][c] = r 행렬부터 c 행렬까지 곱셈 연산 횟수의 최솟값

for(곱셈 연산 할 행렬들의 간격 1 ~ N-1)
	for(r 행렬 0 ~ r행렬+간격 < N)
    	c 행렬 = r + 간격
    	for(k 연산 방법 r ~ c-1)
        	dp[r][c] = min(dp[r][c], dp[r][k]+dp[k+1][c]+m[r].R*m[k].C*m[c].C

Code

const fs = require('fs');
const input = fs.readFileSync('/dev/stdin').toString().split('\n');

const N = +input[0]; // 행렬의 개수 N
const matrix = [];
for (let i = 1; i <= N; i++) matrix.push(input[i].split(' '));

const dp = Array.from({ length: N }, () => new Array(N).fill(Infinity));

// 초기화
for (let i = 0; i < N; i++) dp[i][i] = 0;

for (let interval = 1; interval < N; interval++) {
  for (let start = 0; start + interval < N; start++) {
    let end = start + interval;
    for (let mid = start; mid < end; mid++) {
      dp[start][end] = Math.min(
        dp[start][end],
        dp[start][mid] +
          dp[mid + 1][end] +
          matrix[start][0] * matrix[mid][1] * matrix[end][1]
      );
    }
  }
}

console.log(dp[0][N - 1]);