JavaScript 코딩테스트(7)_핵심 자료구조

Minji Lee·2023년 6월 8일

그래프 리스트 스택 우선순위큐 큐

JS코딩테스트

목록 보기

7/121

자료구조(Data Structure)

다수의 자료(데이터)를 담기 위한 구조

데이터의 수가 많아질수록 효율적인 자료구조가 필요 → 성능 비교

자료구조 종류

1) 선형 구조

배열(array)
연결 리스트(linked list)
스택(stack)
큐(queue)

2) 비선형 구조

트리(tree)
그래프(graph)

선형 자료구조

하나의 데이터 뒤에 다른 데이터가 하나 존재하는 자료구조

→ 데이터가 일렬로 연속적으로(순차적으로) 연결되어 있다.

비선형 자료구조

하나의 데이터 뒤에 다른 데이터가 여러 개 올 수 있는 자료구조

→ 데이터가 일직선상으로 연결되어 있지 않아도 됨

프로그램 성능 측정 방법

시간 복잡도: 알고리즘에 사용되는 연산 횟수 측정
공간 복잡도: 알고리즘에 사용되는 메모리의 양 측정
Big-O 표기법
- 특정한 알고리즘이 얼마나 효율적인지 수치적으로 표현
- 가장 빠르게 증가하는 항만을 고려하는 표기법 ex) O(3n^2+n) = O(n^2)

배열(Array)과 리스트(List)

배열(Array)

가장 기본적인 자료구조
여러 개의 변수를 담는 공간
배열은 인덱스(index)가 존재, 0부터 시작
특정한 인덱스에 직접적으로 접근 가능 → 수행 시간: O(1)

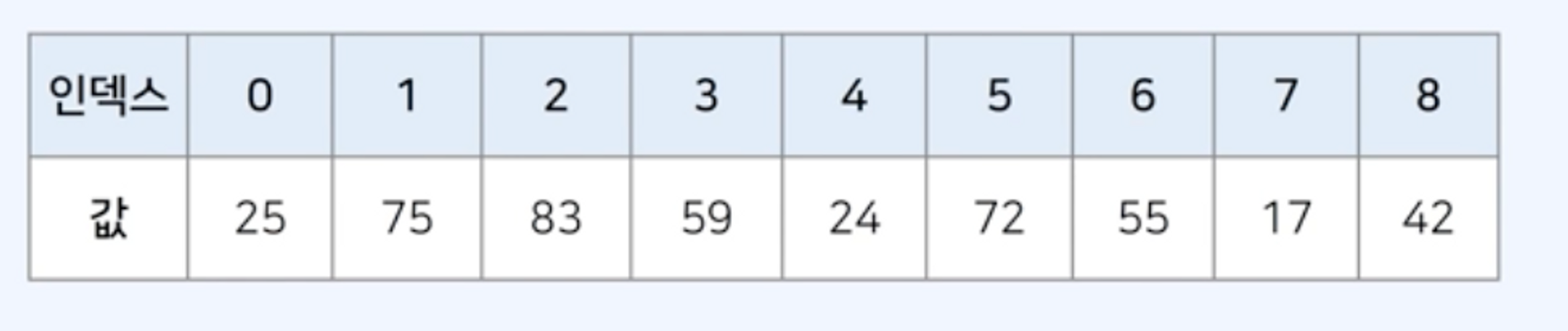
[특징]

컴퓨터의 메인 메모리에서 배열 공간은 연속적으로 할당됨
장점: 캐시(cache) 히트 가능성 높음, 조회 빠름
단점: 배열 크기를 미리 지정해야 하므로, 데이터 추가 및 삭제에 한계 존재

연결 리스트(Linked List)

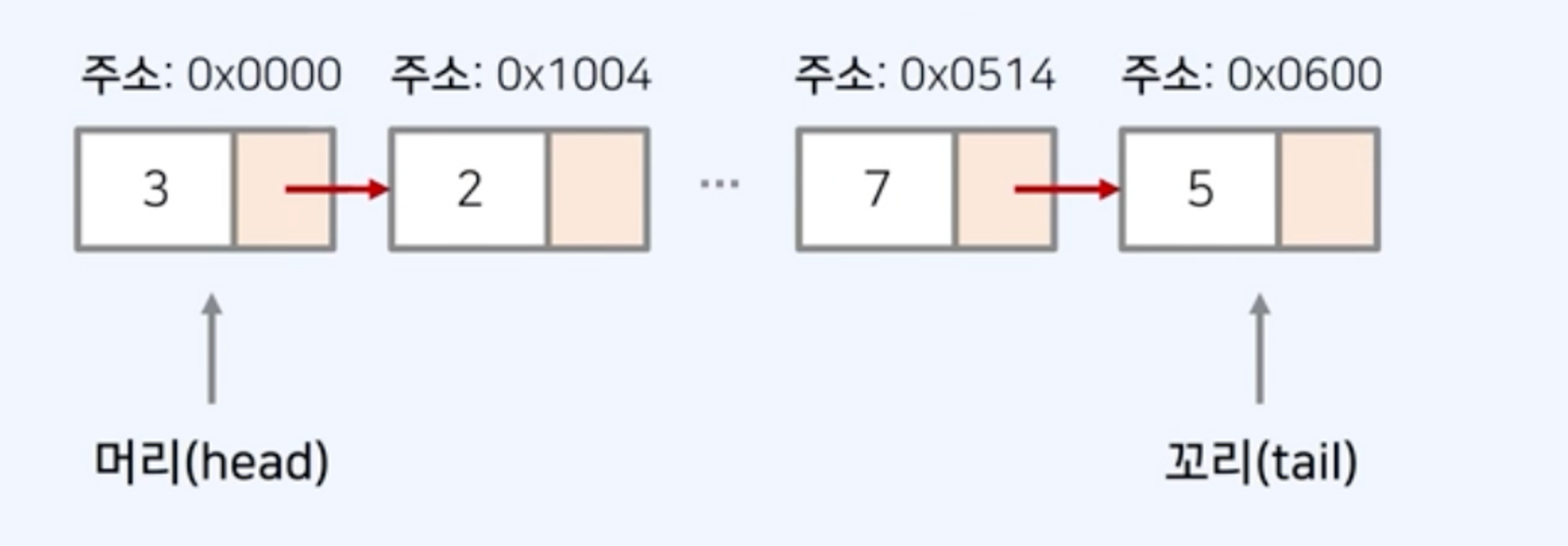
컴퓨터의 메인 메모리상에서 주소가 연속적이지 않다.
배열과 다르게 크기가 정해져 있지 않고, 리스트의 크기는 동적으로 변경 가능
장점: 포인터(pointer)를 통해 다음 데이터의 위치를 가리키기 때문에 삽입과 삭제가 간편
단점: 특정 번째의 원소를 검색할 때는 앞에서부터 원소를 찾아야 하므로, 데이터 검색 속도가 느림

JavaScript가 제공하는 배열 기능

동적 배열
배열 용량 가득차면, 자동으로 크기 증가시킴
배열 혹은 스택의 기능 필요할 때 사용 가능
큐의 기능은 제공 못함(비효율적)

배열 초기화

1) 대괄호 사용

// 빈 배열 생성
let arr = [];

arr.push(7);
arr.push(8);
arr.push(9);

for (let i=0;i<arr.length;i++){
	console.log(arr[i]);
}
// 7
// 8
// 9

2) Array() 사용

// 빈 배열 생성
let arr = new Array();

arr.push(7);
arr.push(8);
arr.push(9);

for (let i=0;i<arr.length;i++){
	console.log(arr[i]);
}
// 7
// 8
// 9

3) 임의의 크기를 가지는 배열 생성

// 원하는 값을 직접 입력하여 초기화
let arr1 = [0,1,2,3,4];
console.log(arr1);
// [0,1,2,3,4]

// 하나의 값으로 초기화
let arr2 = Array.from({length: 5}, () => 7);
console.log(arr2);
// [7,7,7,7,7]

4) 2차원 리스트(배열) 만들기

// 원하는 값을 직접 입력하여 초기화
let arr1 = [
	[0,1,2,3],
	[4,5,6,7],
	[8,9,10,11]
];
console.log(arr1);

5) ES6이상부터 사용할 수 있는 2차원 배열 생성

// 빈 배열 생성
let arr = Array.from(Array(4), () => new Array(5))
console.log(arr);

/*
[
	[ <5 empty items> ],
	[ <5 empty items> ],
	[ <5 empty items> ],
	[ <5 empty items> ]
]
*/

6) 반복문 이용하여 2차원 배열 초기화

let arr2 = new Array(3);
for (let i=0;i<arr2.length;i++){
	arr2[i] = Array.from(
		{length: 4},
		(undefined, j) => i*4+j
	);
}
console.log(arr2);
/*
[
	[0,1,2,3],
	[4,5,6,7],
	[8,9,10,11]
]
*/

7) 배열 생성 후에도 배열의 크기 임의로 변경 가능, push() 메서드 이용하여 배열 가장 뒤쪽에 새로운 원소 추가

let arr2 = [5,6,7,8,9];
arr.length=8;
arr[7]=3;
arr.push(1);

for (let x of arr){
	console.log(x);
}
/*
5
6
7
8
9
undefined
undefined
3
1
*/

JS 배열의 대표적인 메서드

1) concat(): 여러 개의 배열을 이어 붙여서 합친 결과 반환 → **O(N)**

let arr1 = [1,2,3,4,5];
let arr2 = [6,7,8,9,10];
let arr = arr1.concat(arr2, [11,12], [13]);
console.log(arr);

/*
[
	1,2,3,4,5,6,
	7,8,9,10,11,12,13
]
*/

2) slice(left, right): 특정 구간의 원소를 꺼낸 배열을 반환 → O(N)

left부터 right-1까지의 원소를 꺼냄

let arr = [1,2,3,4,5];
let result = arr.slice(2,4);

console.log(result);
// [3,4]

3) indexOf(): 특정한 값을 가지는 원소의 첫째 인덱스를 반환 → O(N)

해당하는 원소가 없는 경우 -1을 반환

let arr = [7,3,5,6,6,2,1];

console.log(arr.indexOf(5));
console.log(arr.indexOf(6));
console.log(arr.indexOf(8));

// 2
// 3
// -1

연결 리스트(Linked List)

각 노드가 한 줄로 연결되어 있는 자료구조

각 노드는 (데이터, 포인터) 형태를 가짐
포인터: 다음 노드의 메모리 주소를 가리키는 목적으로 사용

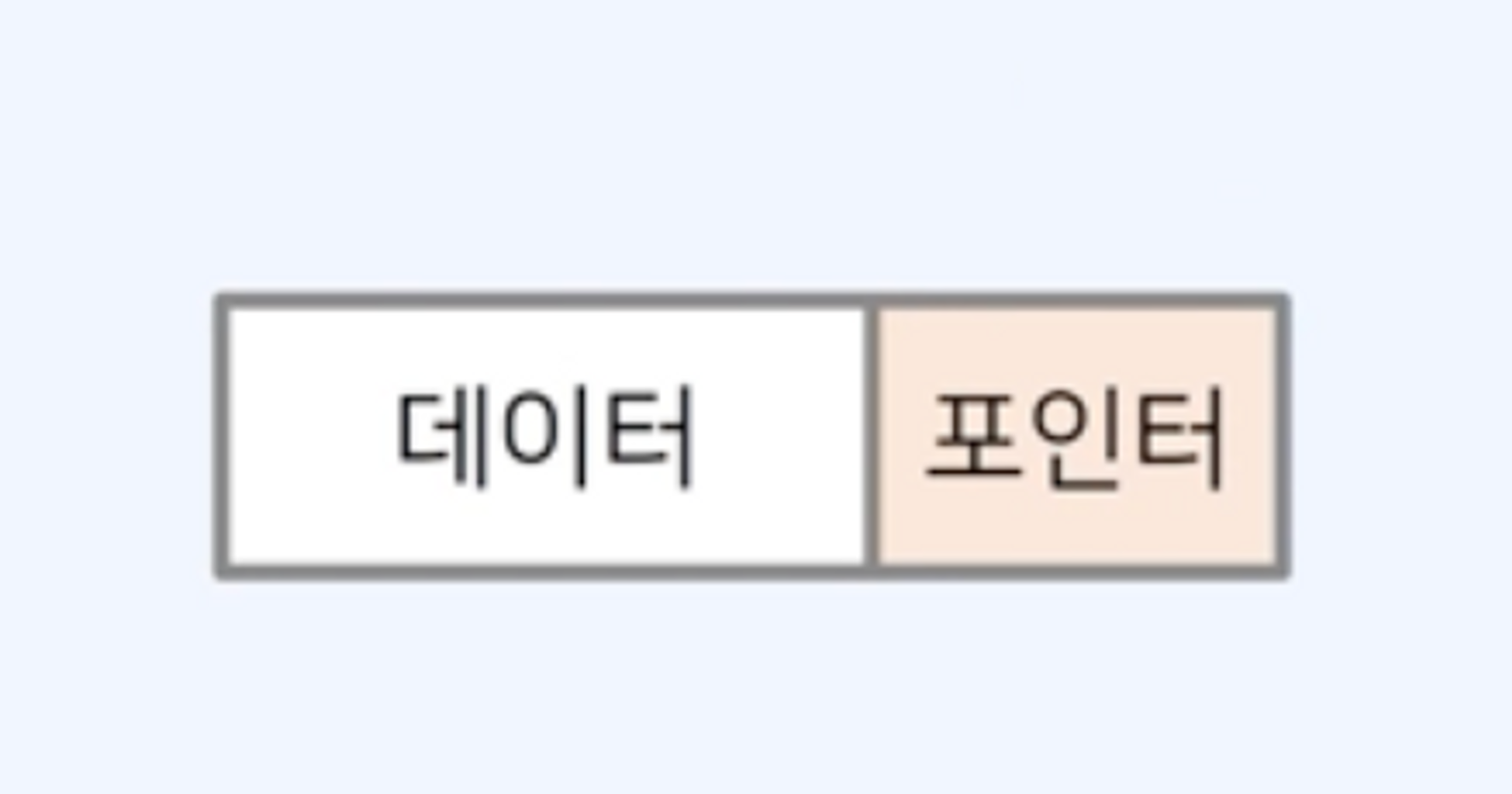
연결리스트 이용하여 다양한 자료구조 구현 가능 → ex) 스택, 큐 등
JS는 연결 리스트 활용하는 자료구조 제공

연결 리스트 vs 배열

특정 위치의 데이터를 삭제할 때는 배열에서는 O(N)만큼 시간 소요
- 중간에 빈 배열이 없도록 이동시켜줘야 하기 때문에
연결리스트는 단순히 연결만 끊어주면 되므로 삭제할 위치 정확하게 알고 있는 경우 O(1) 시간 소요

스택(Stack)

먼저 들어온 데이터가 나중에 나가는 자료구조 → FILO

스택이 제공하는 연산

삽입(push): 스택에 원소를 삽입하는 연산(마지막 위치에 삽입) → O(1)

추출(pop): 스택에 원소를 추출하는 연산(마지막 위치 추출) → O(1)

최상위 원소(top): 스택의 최상위 원소(마지막에 들어온 원소)를 확인하는 연산 → O(1)

Empty: 스택이 비어 있는지 확인하는 연산 → O(1)

JS가 제공하는 메서드

push(): 마지막 위치에 원소 삽입

pop(): 마지막 위치에서 원소 추출

스택 구현할 때, 배열 자료형 사용

ex)

let stack = [];

stack.push(5);
stack.push(2);
stack.push(1);
stack.pop();
stack.push(4);

let reversed = stack.slice().reverse();
console.log(reversed); // 최상단 원소부터 출력
console.log(stack);
// [1,3,2,5]
// [5,2,3,1]

연결리스트로 스택 구현

삽입: 머리(head) 위치에 데이터 넣음
삭제: 머리(head) 위치에서 데이터 꺼냄

큐(Queue)

먼저 삽입된 데이터가 먼저 추출되는 자료구조 → FIFO

꼬리 위치에 데이터가 삽입되고, 머리 위치에서 삭제됨
큐는 배열로 구현하면 안됨
큐를 연결리스트로 구현하면, 삽입과 삭제가 O(1) 보장
연결 리스트로 구현할 때, 머리(head)와 꼬리(tail) 두개의 포인터 가짐
머리(head): 남아 있는 원소 중 가장 먼저 들어 온 데이터를 가리키는 포인터
꼬리(tail): 남아있는 원소 중 가장 마지막에 들어 온 데이터를 가리키는 포인터

연결리스트로 큐 구현

삽입: 꼬리(tail)위치에 데이터 넣기
삭제: 머리(head)위치에서 데이터 꺼내기
js에서는 Dictionary 자료형 이용하여 큐 구현하면 간단함

JS로 큐 구현하기

1) 큐 클래스 생성하여 사용

class Queue{
	constructor(){
		this.items = {};
		this.headIndex = 0;
		this.tailIndex = 0;
	}
	enqueue(item){
		this.items[this.tailIndex] = item;
		this.tailIndex++;
	}
	dequeue(){
		const item = this.items[this.headIndex];
		delete this.items[this.headIndex];
		this.headIndex++;
		return item;
	}
	peek(){
		return this.items[this.headIndex];
	}
	getLength(){
		return this.tailIndex - this.headIndex;
	}
}

2) 큐 라이브러리 사용

queue = new Queue();

queue.enqueue(5);
queue.enqueue(2);
queue.enqueue(3);
queue.dequeue();

// 큐가 비어있지 않을 때까지 반복
while (queue.getLength() != 0){
	console.log(queue.dequeue());
}

// 2
// 3

트리(Tree)와 우선순위 큐(Priority Queue)

트리: 가계도와 같이 계층적인 구조를 표현할 때 사용할 수 있는 자료구조

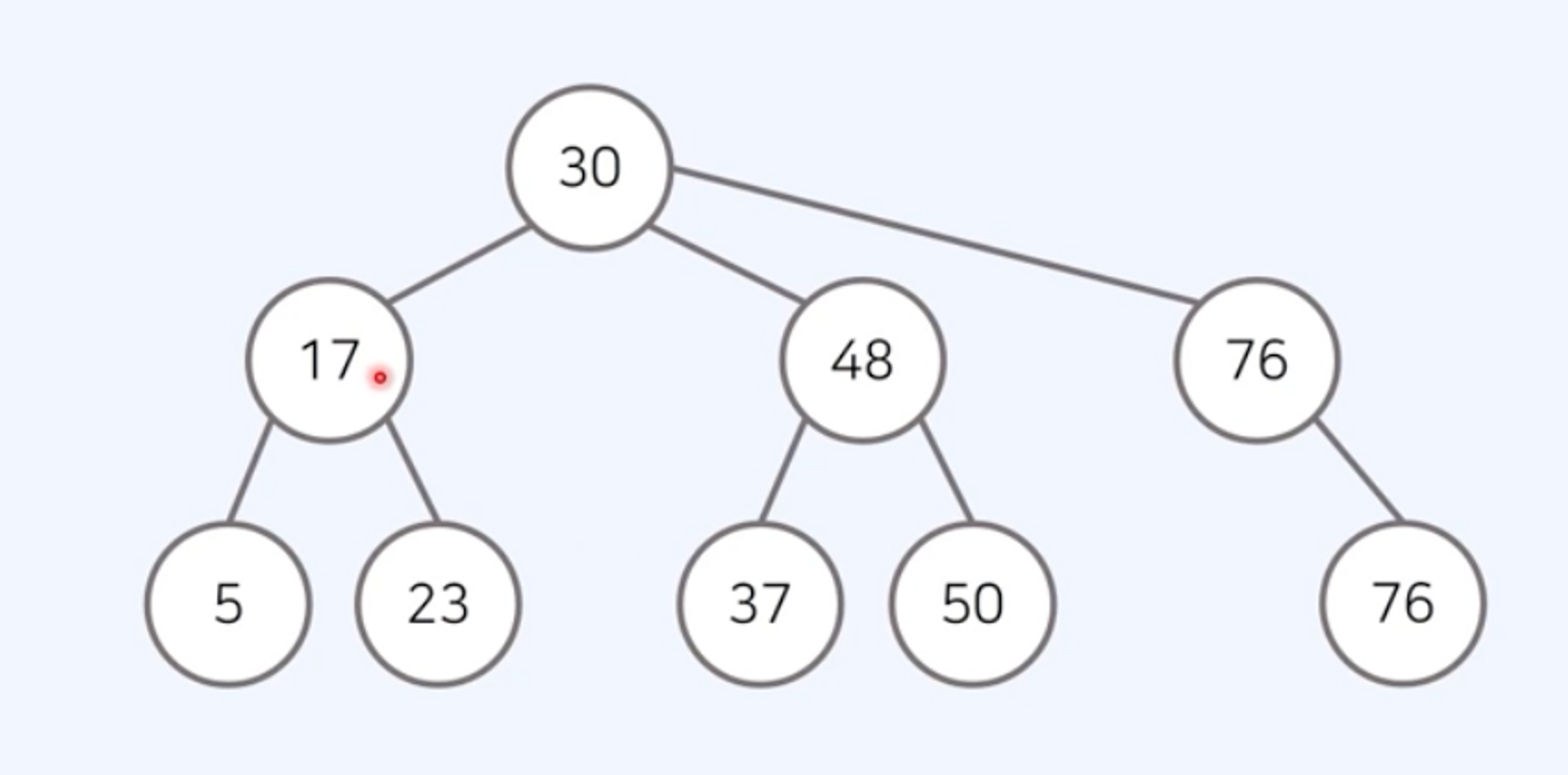
각각의 노드는 여러 개의 자식 노드 가짐

트리 용어

루트 노드(root node): 부모가 없는 최상위 노드
단말 노드(leaf node): 자식이 없는 노드

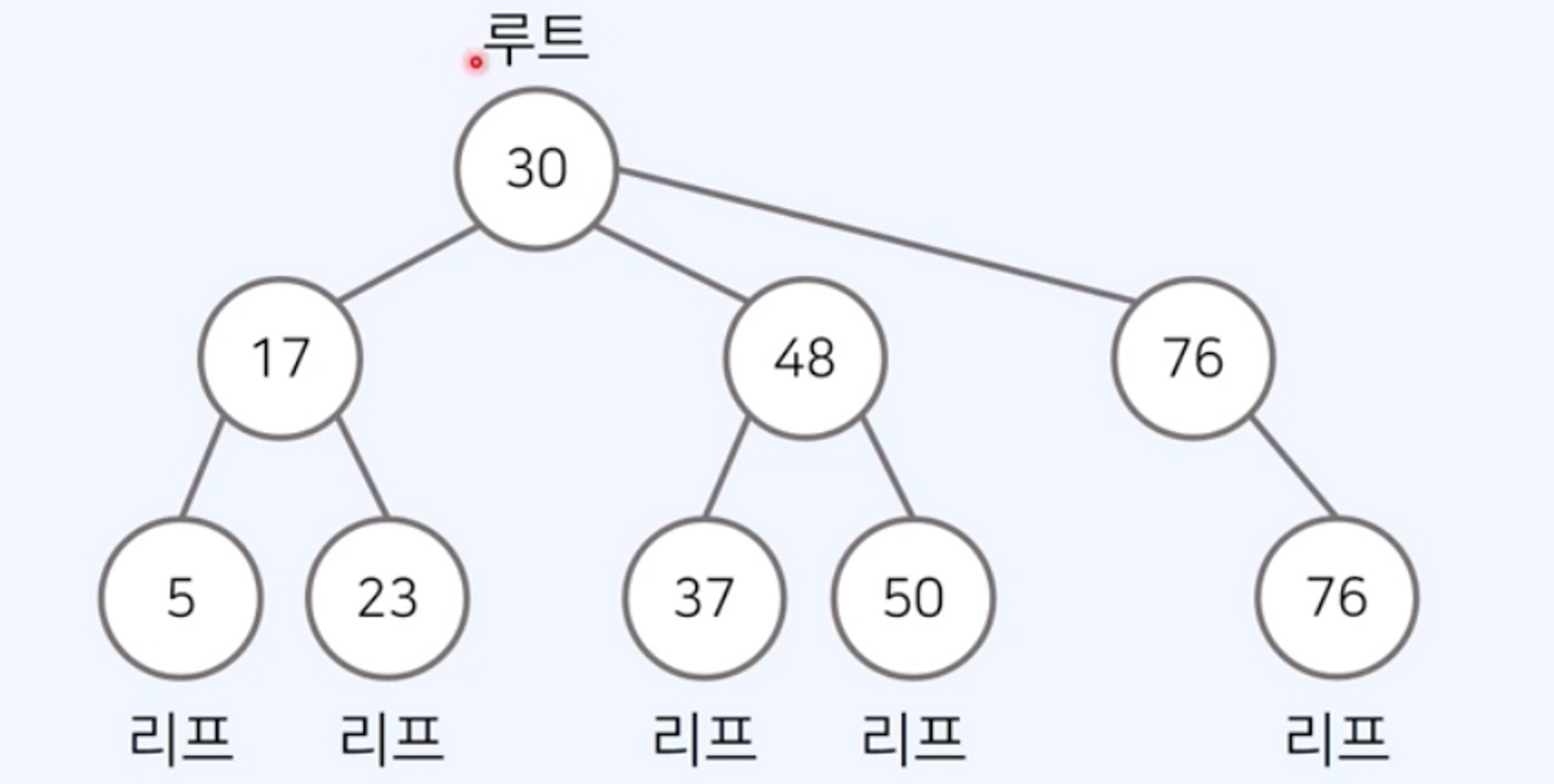
트리에서는 부모와 자식 관계 성립함
형제 관계: 같은 부모를 가지고 있는 노드들
깊이(depth): 루트 노드에서의 길이(length)
길이: 출발 노드에서 목적지 노드까지 거쳐야 하는 간선의 수를 의미
트리의 높이는 루트 노드에서 가장 깊은 노드까지의 길이 의미

이진 트리(Binary Tree)

최대 2개의 자식을 가질 수 있는 트리

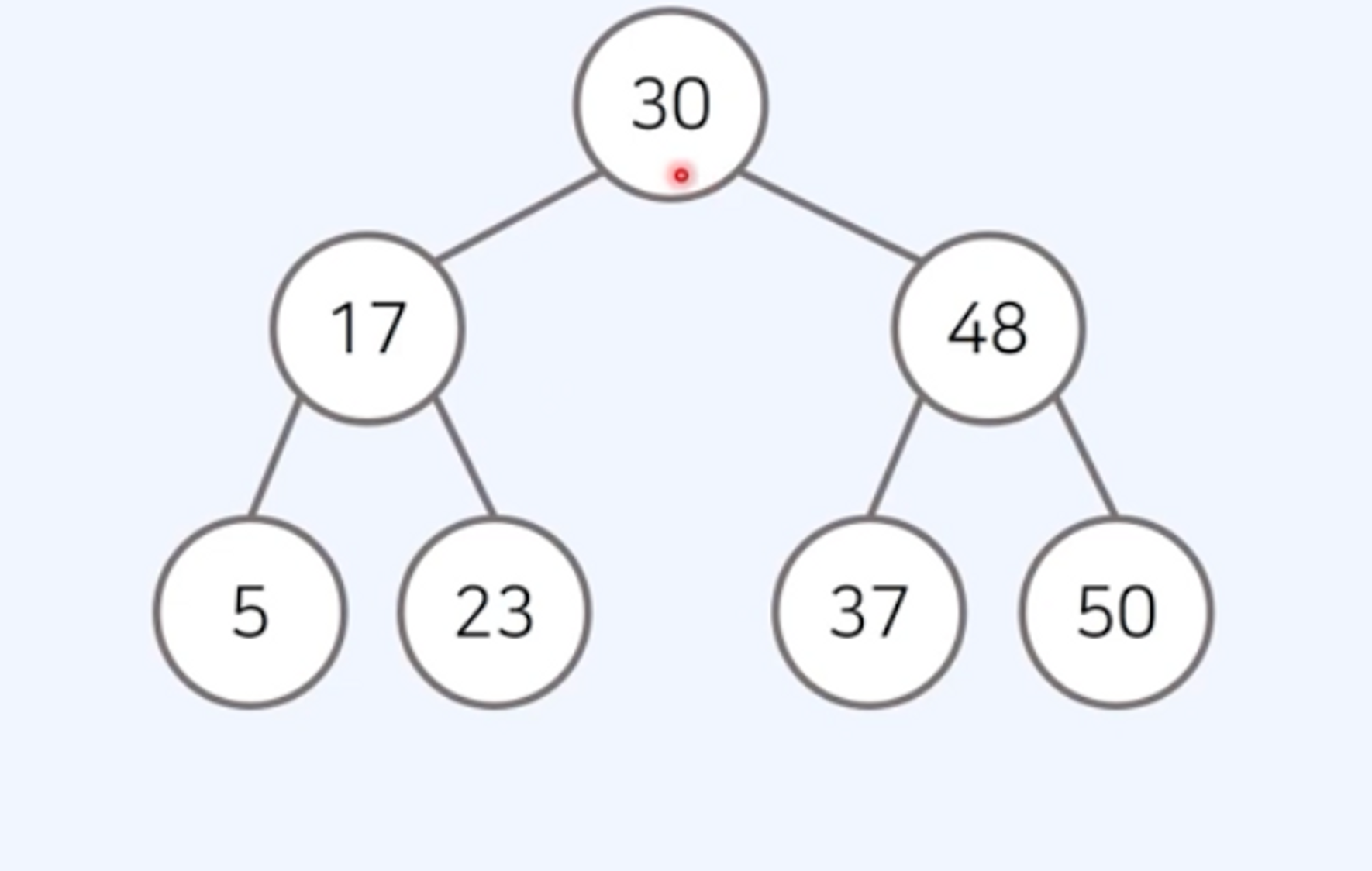
포화 이진 트리(Full Binary Tree): 리프 노드를 제외한 모든 노드가 두 자식을 가지고 있는 트리
완전 이진 트리(Complete Binary Tree): 모든 노드가 왼쪽 자식부터 차근차근 채워진 트리

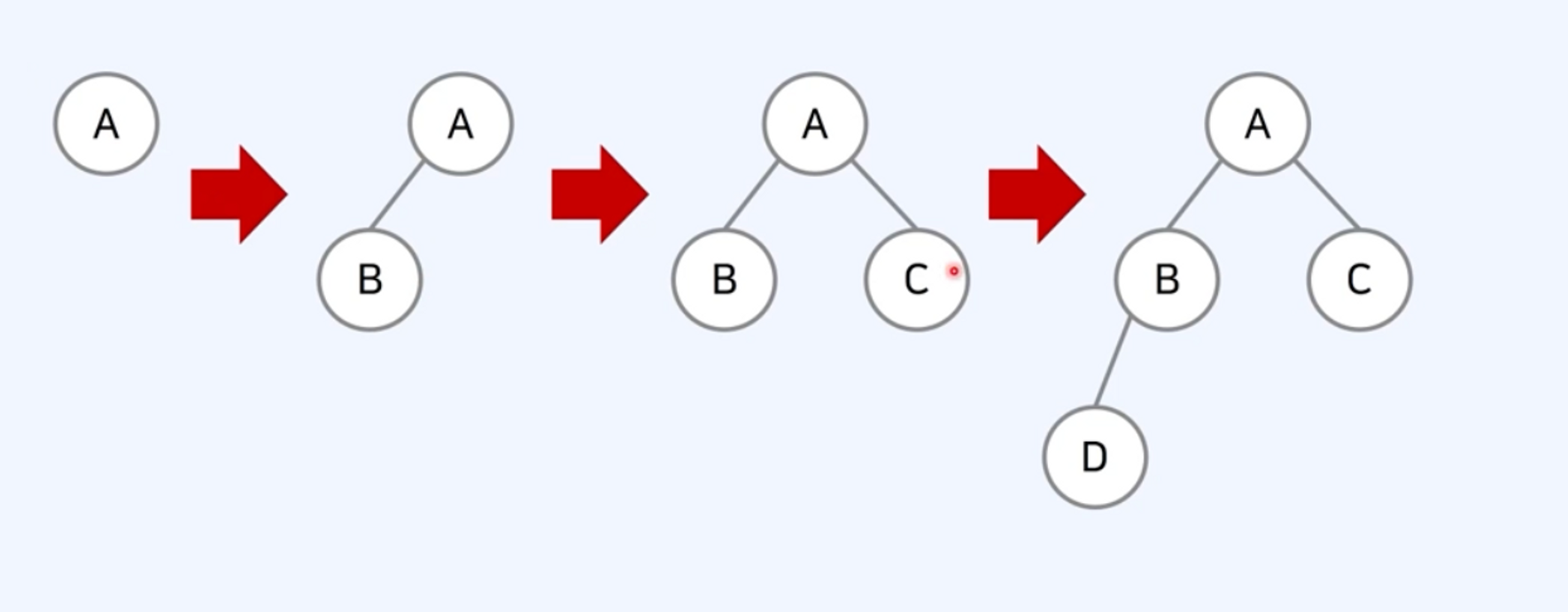
높이 균형 트리(Height Balanced Tree): 왼쪽 자식 트리와 오른쪽 자식 트리의 높이가 1이상 차이나지 않는 트리

우선순위 큐(Priority Queue)

우선순위에 따라서 데이터를 추출하는 자료구조

힙(heap)을 이용해 구현

힙(Heap)

원소들 중에서 최댓값 혹은 최솟값을 빠르게 찾아내는 자료구조

최대 힙: 값이 큰 원소부터 추출
최소 힙: 값이 작은 원소부터 추출
힙은 원소의 삭제와 삽입을 위해 O(logN) 수행 시간 요구
단순한 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일 → O(NlogN)

최대 힙(max heap): 부모 노드가 자식 노드보다 값이 큰 완전 이진 트리

루트 노드가 전체 트리에서 가장 큰 값을 가짐

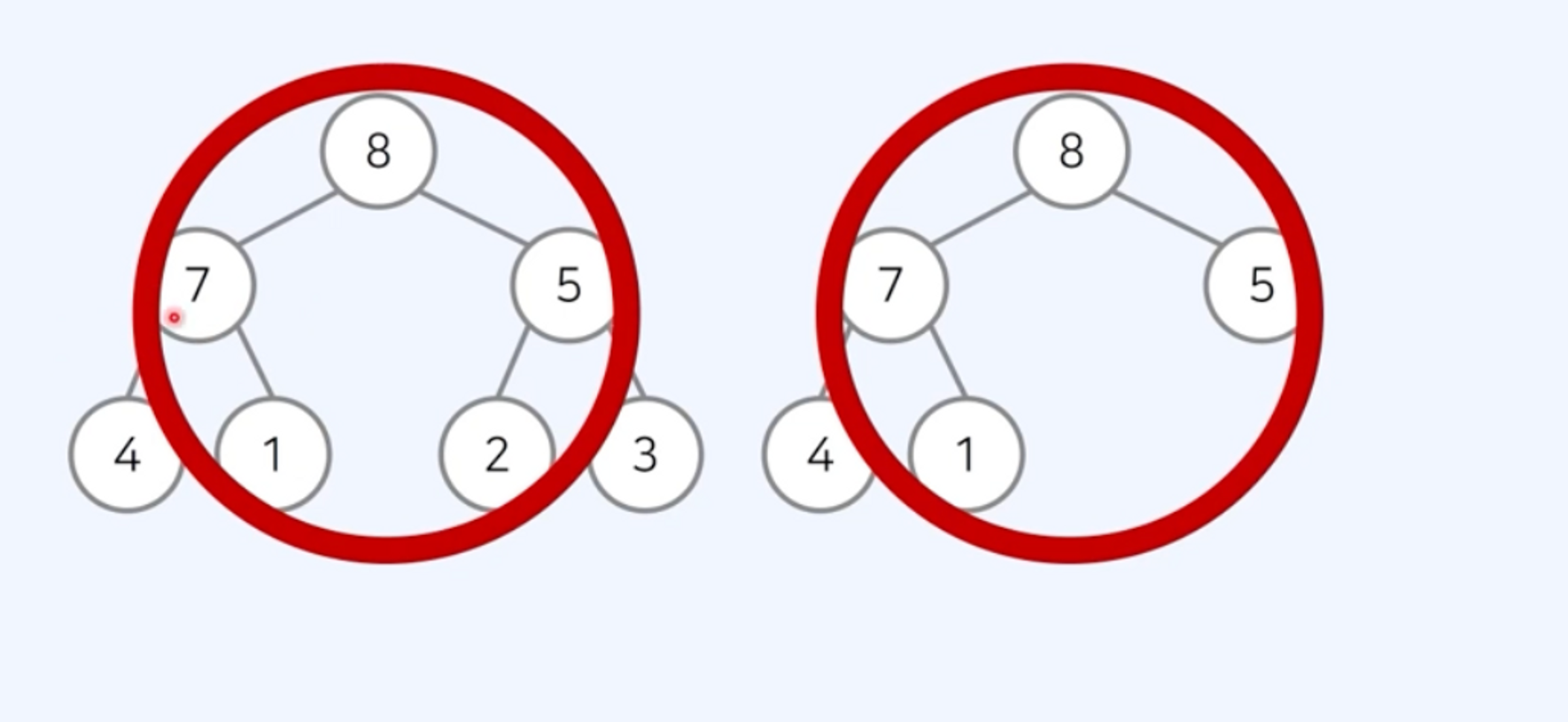
힙의 특징

완전 이진 트리 자료구조 따름
힙에서는 우선순위가 높은 노드가 루트에 위치
최대 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 크다
- 루트 노드가 가장 크며, 값이 큰 데이터가 우선순위를 가짐
최소 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작다
- 루트 노드가 가장 작으며, 값이 작은 데이터가 우선순위를 가짐

구현 방식

리스트 자료형: 삽입 시간 O(1), 삭제 시간 O(N)
힙: 삽입 시간 O(logN), 삭제 시간 O(logN)

우선순위 큐 구현 방법

일반적인 형태의 큐는 선형적인 구조 가짐
우선 순위 큐는 이진 트리 구조를 사용하는 것이 일반적

최소 힙 구성 함수: `Heapify`

(상향식) 부모로 거슬러 올라가며, 부모보다 자신이 더 작은 경우 위치 교체

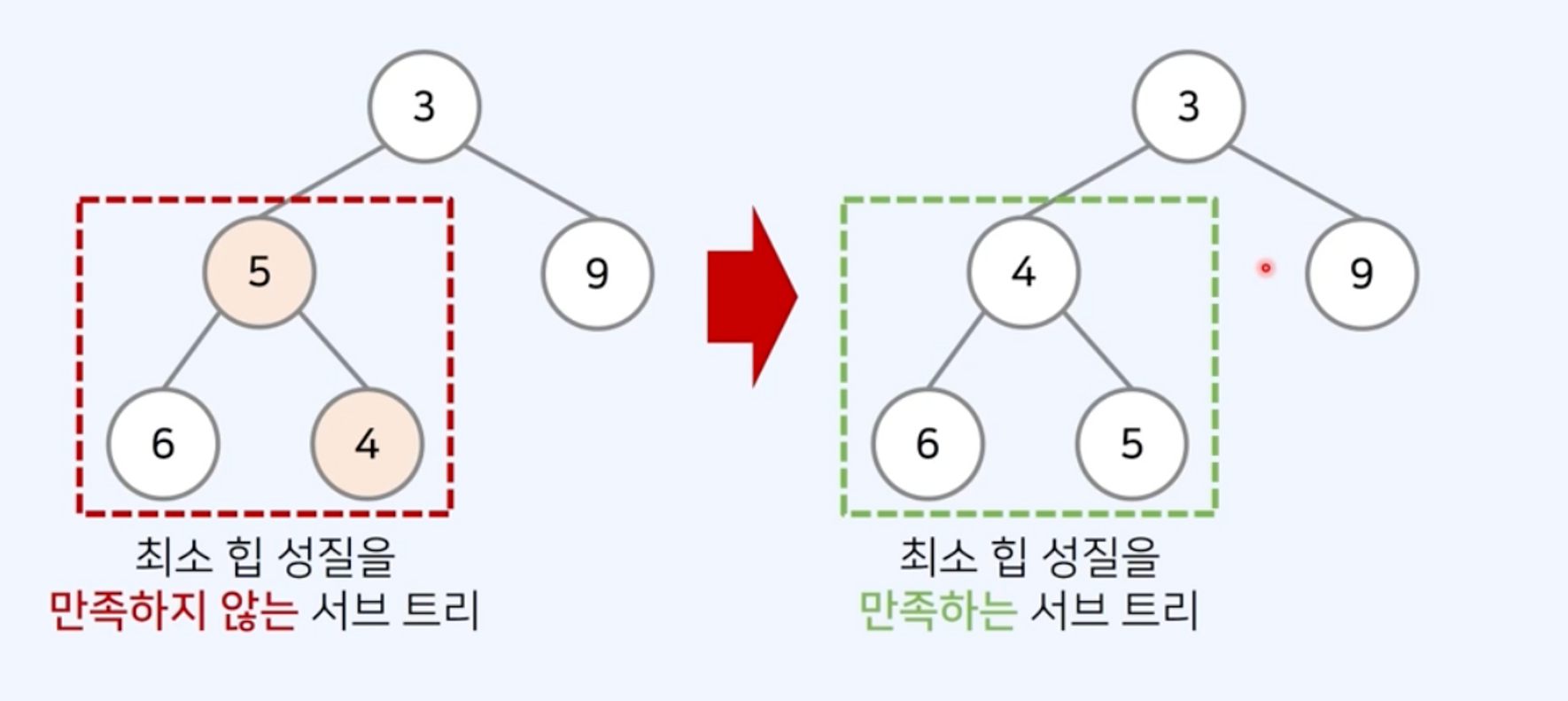
원소 삭제될 때, 가장 마지막 노드가 루트 노드의 위치에 오도록 하고, 루트 노드부터 하향식으로 heapify() 진행

힙의 특징

힙의 삽입과 삭제 연산을 수행할 때, 처리해야 하는 범위에 포함된 원소의 개수가 절반씩 줄어든다. → O(logN)

JS의 힙 라이브러리

JS는 우선순위 큐를 라이브러리로 제공 안함

힙이 필요한 경우 별도의 라이브러리 사용해야함

https://github.com/ndb796/priorityqueuejs/blob/master/index.js

// 최대 힙
let pq = new PriorityQueue(function(a,b) {
	return a.cash - b.cash;
});

pq.enq({cash:250, name:'Doohyun Kim'});
pq.enq({cash:300, name:'Gildong Hong'});
pq.enq({cash:150, name:'Minchul Han'});
console.log(pq.size()); // 3
console.log(pq.deq()); // {cash:300, name:'Gildong Hong'}
console.log(pq.peek()); // {cash:250, name:'Doohyun Kim'}
console.log(pq.size()); // 2

그래프(Graph)의 표현

사물을 정점(vertex)(=노드)과 간선(edge)으로 나타내기 위한 도구

구현 방식
- 인접 행렬: 2차원 배열 사용하는 방식
- 인접 리스트: 연결 리스트를 이용하는 방식

인접 행렬(Adjacency Matrix)

2차원 배열로 표현

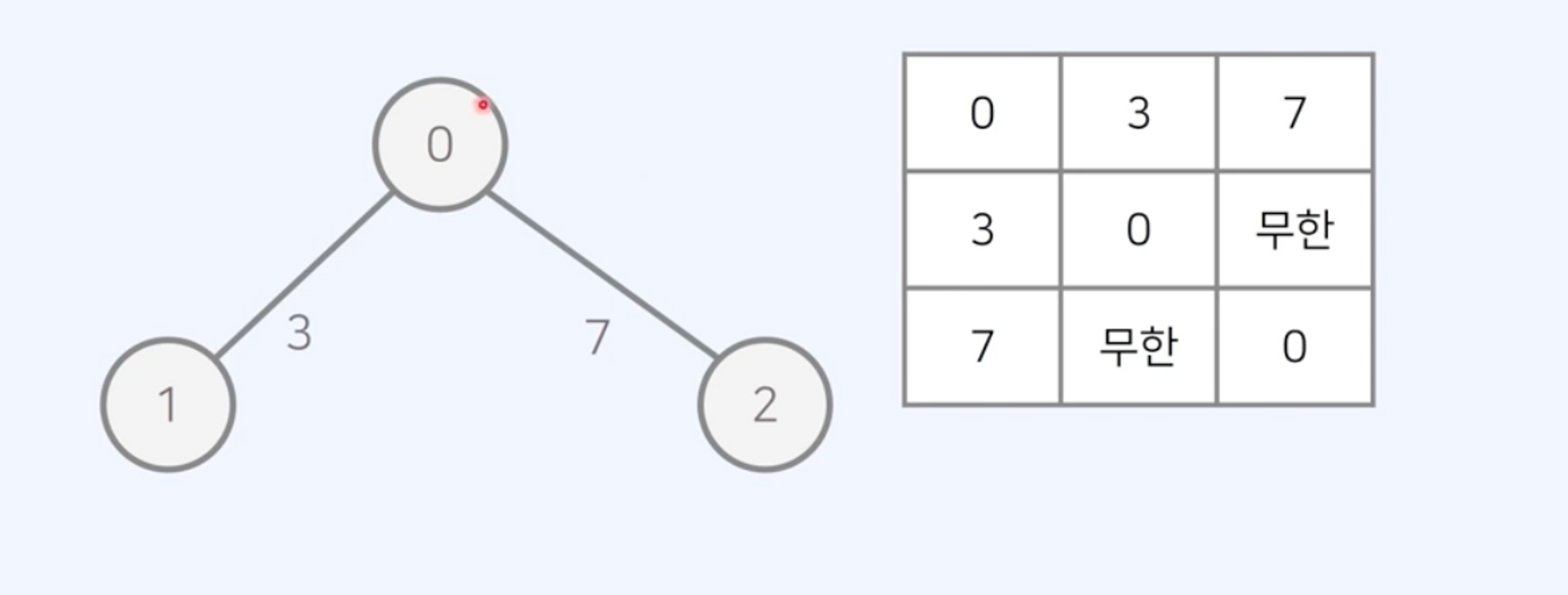
→ 행이 시작 노드, 열이 도착 노드 → 드는 비용 표시

무방향 무가중치 그래프
- 무방향 그래프: 모든 간선이 방향성을 가지지 않는 그래프
- 무가중치 그래프: 모든 간선에 가중치가 없는 그래프

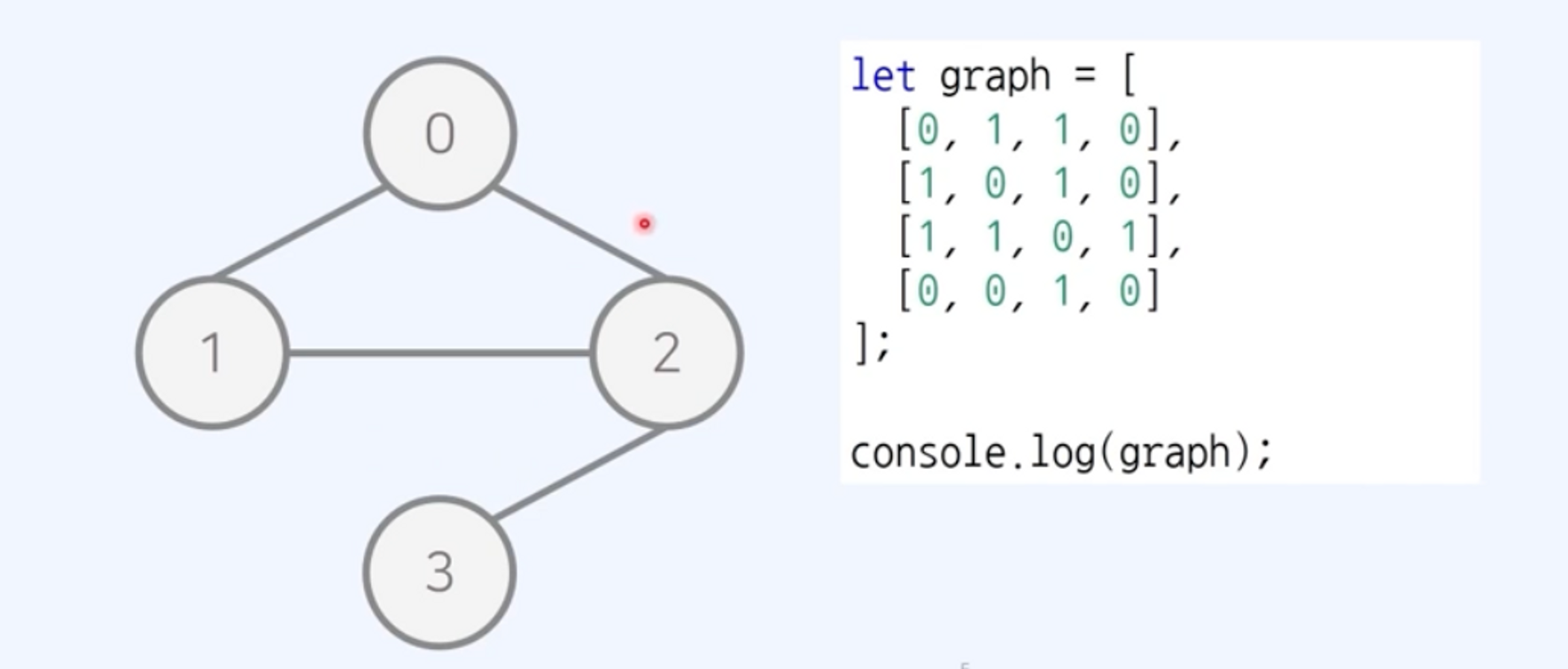
방향 가중치 그래프
- 방향 그래프: 모든 간선이 방향을 가지는 그래프
- 가중치 그래프: 모든 간선에 가중치가 있는 그래프

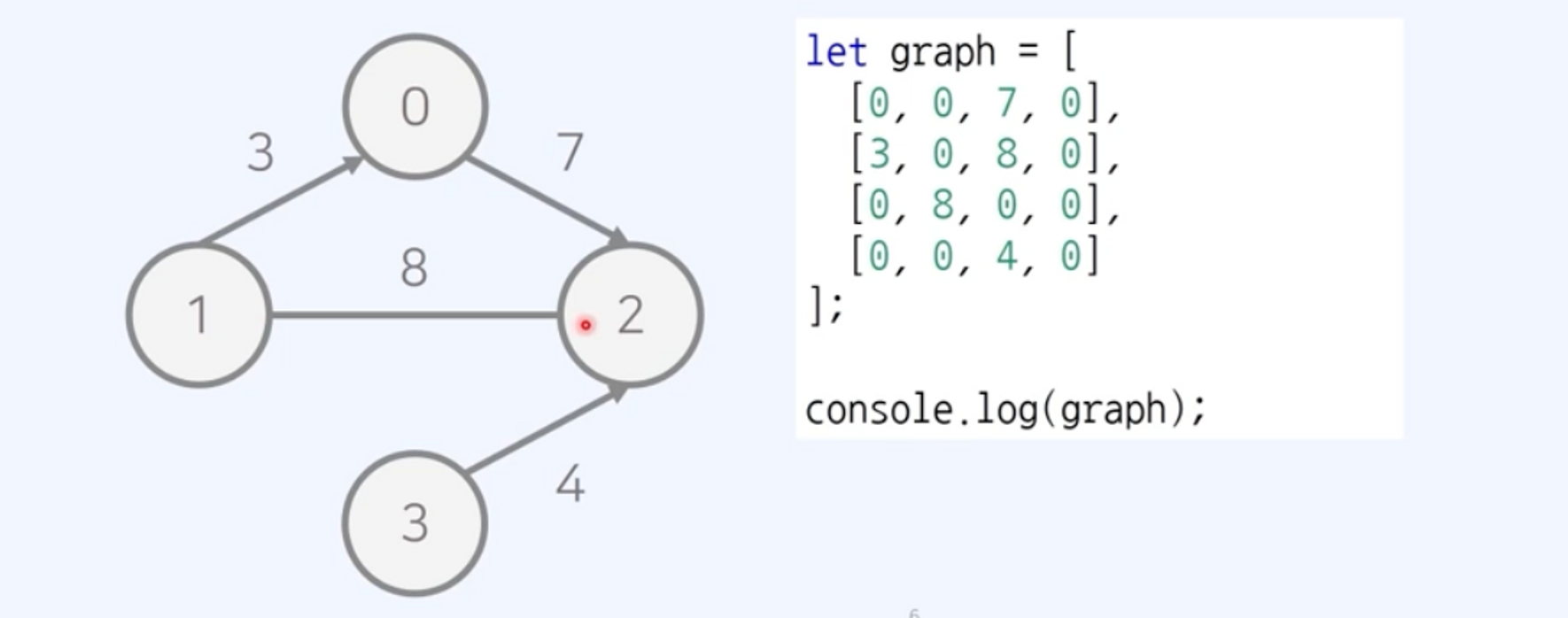
모든 정점들의 연결 여부를 저장해 O(V^2)의 공간 요구
- 공간 효율성 떨어짐
- 두 노드의 연결 여부를 O(1)에 확인 가능

인접 리스트(Adjacency List)

리스트로 표현

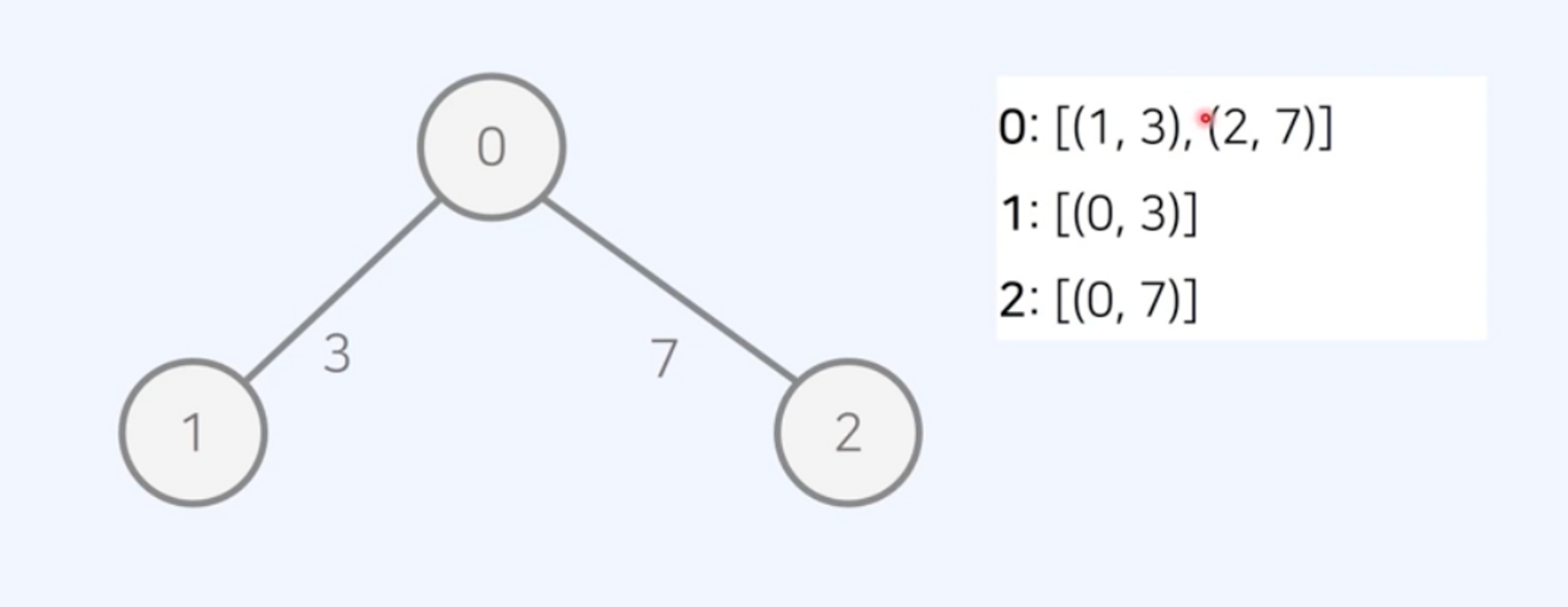
무방향 무가중치 그래프

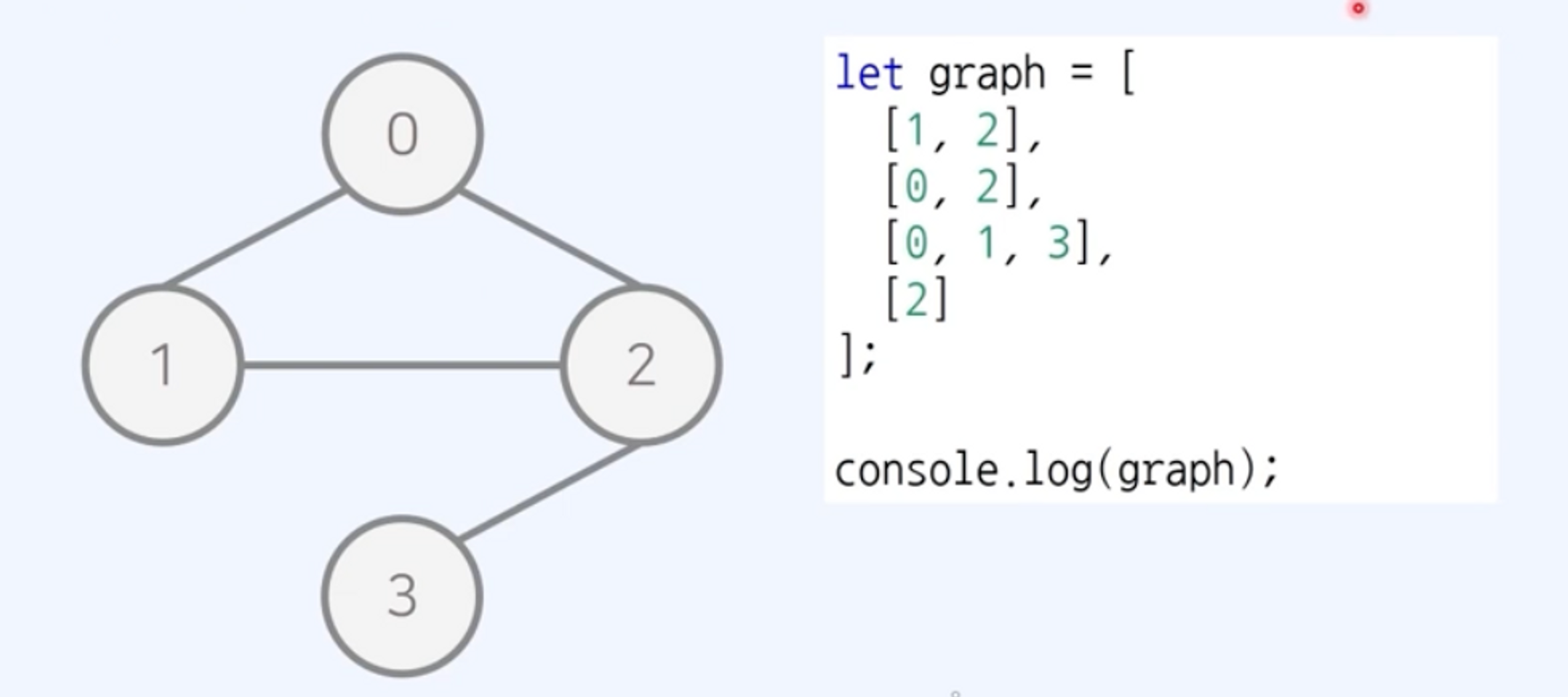
방향 가중치 그래프

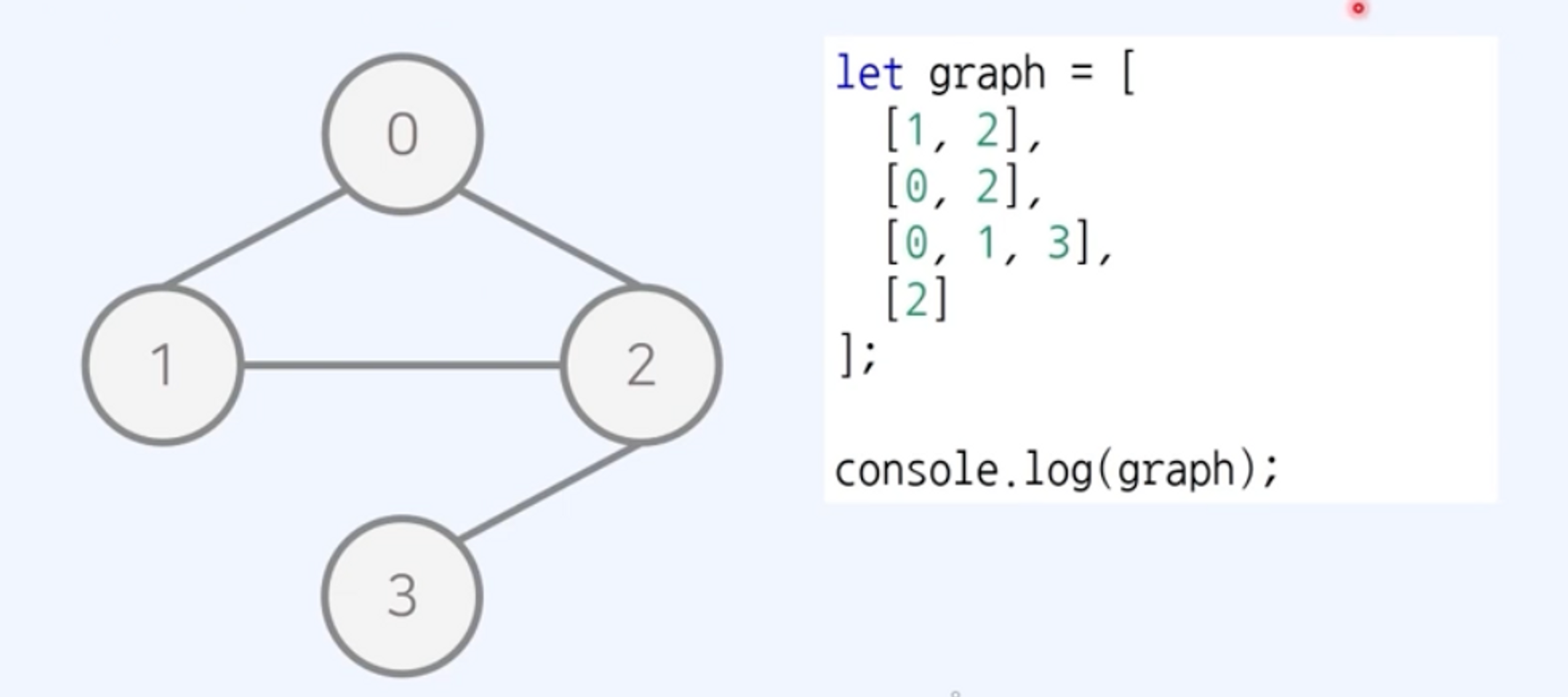
연결된 간선의 정보만을 저장하여 O(V+E)의 공간 요구
- 공간 효율성 우수
- 두 노드의 연결 여부를 O(V)시간 필요

인접 행렬 vs 인접 리스트

각각 근처의 노드와 연결되어 있는 경우가 많으므로, 간선 개수가 적어 인접 리스트가 유리

Minji Lee

이전 포스트

JavaScript 코딩테스트(6)_문자열 문제

다음 포스트

JavaScript 코딩테스트(7)_핵심 자료구조

JS코딩테스트

자료구조(Data Structure)

다수의 자료(데이터)를 담기 위한 구조

자료구조 종류

선형 자료구조

비선형 자료구조

프로그램 성능 측정 방법

배열(Array)과 리스트(List)

배열(Array)

연결 리스트(Linked List)

JavaScript가 제공하는 배열 기능

배열 초기화

JS 배열의 대표적인 메서드

연결 리스트(Linked List)

연결 리스트 vs 배열

스택(Stack)

먼저 들어온 데이터가 나중에 나가는 자료구조 → FILO

스택이 제공하는 연산

JS가 제공하는 메서드

연결리스트로 스택 구현

큐(Queue)

먼저 삽입된 데이터가 먼저 추출되는 자료구조 → FIFO

연결리스트로 큐 구현

JS로 큐 구현하기

트리(Tree)와 우선순위 큐(Priority Queue)

트리: 가계도와 같이 계층적인 구조를 표현할 때 사용할 수 있는 자료구조

트리 용어

이진 트리(Binary Tree)

우선순위 큐(Priority Queue)

힙(Heap)

최대 힙(max heap): 부모 노드가 자식 노드보다 값이 큰 완전 이진 트리

힙의 특징

구현 방식

우선순위 큐 구현 방법

최소 힙 구성 함수: Heapify

힙의 특징

JS의 힙 라이브러리

그래프(Graph)의 표현

사물을 정점(vertex)(=노드)과 간선(edge)으로 나타내기 위한 도구

인접 행렬(Adjacency Matrix)

인접 리스트(Adjacency List)

인접 행렬 vs 인접 리스트

JavaScript 코딩테스트(6)_문자열 문제

JS코딩테스트 문제풀이(Daily Temperatures)

0개의 댓글

최소 힙 구성 함수: `Heapify`