DP(다이나믹 프로그래밍, 동적계획) 알고리즘

Minji Lee·2023년 11월 10일
DPjs동적계획
0

JS코딩테스트

목록 보기
29/156
post-thumbnail

다이나믹 프로그래밍

  • 메모리를 더 사용하여 시간복잡도 개선할 때 사용됨
  • 점화식을 찾는 것이 핵심적!

사용 되는 조건

  1. 최적 부분 구조
    • 큰 문제를 유사한 형태의 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아 큰 문제 해결
  2. 반복되는 부분 문제
    • 동일한 작은 문제를 반복적으로 해결

ex) 피보나치 수열 예시

[1, 1, 2, 3, 5, 8, 13, 21, 35, …] → ana_n = an−1a_{n-1}+an−2a_{n-2} (a1a_1 = 1, a2a_2 = 1)

💡 점화식 구성요소
1. 초기항
2. 인접한 항과의 관계

  • 점화식은 [재귀 함수]로 표현할 수 있음
  • 재귀함수는 [종료 조건]이 있어야 하는데, 이것이 점화식의 초기항과 같은 역할 수행
// 피보나치 함수를 재귀함수로 표현
function fibo(x) { 
	if (x == 1 || x ==2){ // 종료조건이 없으면 무한 루프
		return 1;
	}
	return fibo(x-1) + fibo(x-2); // 실질적인 점화식 부분
}

console.log(fibo(4));

→ 점화식을 그대로 재귀함수로 구현하면 중복되는 부분 문제 발생!(이미 구한 값을 불필요하게 반복 계산) ⇒ DP로 문제 해결가능!

d = new Array(100).fill(0); // 한 번 계산된 결과를 **메모이제이션**하기 위해 리스트 쵝화
function fibo(x){
	if(x == 1 || x ==2){
			return 1;
	}
	// 이미 계산한 적 있는 문제라면 그래도 반환
	if(d[x] != 0){
		return d[x];
	}
	// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
	d[x] = fibo(x-1) + fibo(x-2);
	return d[x];
}
console.log(fibo(99));

❗️DP의 대표적인 코드 형식

function dp() {
	1. 종료 조건
	2. 이미 해결한 문제라면, 정답을 그래도 반환
	3. 점화식에 따라 정답 계산
}

DP 문제 해결 접근 순서

  1. 문제 이해
  2. 점화식 찾아내기 → 핵심!
  3. 구현방식(상향식/하향식) 결정
    • 상향식(bottom-up): 반복문을 이용해 초기 항 부터 계산
      d = new Array(100).fill(0); // DP ㄷ테이블 초기화

// 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1;
d[2] = 1;
n = 99;

// 피보나치 함수 반복문으로 구현
for (let i=3; i <= n; i++) {
	d[i] = d[i-1] + d[i-2];
}

console.log(d[n]);
    • 하향식(top-down): 재귀 함수로 큰 항을 구하기 위해 작은(이전) 항을 호출하는 방식
      d = new Array(100).fill(0);

function fibo(x) {
	if (x == 1 || x == 2){
		return 1;
	}
	// 이미 계산한 적 있는 문제라면 그래도 반환
	if(d[x] != 0){
		return d[x];
	}
	// 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
	d[x] = fibo(x-1) + fibo(x-2);
	return d[x];
}
console.log(fibo(99));
  4. 점화식을 실제 코드로 구현

문제풀이

1. 피보나치 함수(1003)

문제

다음 소스는 N번째 피보나치 수를 구하는 C++ 함수이다.

int fibonacci(int n) {
    if (n == 0) {
        printf("0");
        return 0;
    } else if (n == 1) {
        printf("1");
        return 1;
    } else {
        return fibonacci(n‐1) + fibonacci(n‐2);
    }
}

fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.

  • fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
  • fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
  • 두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
  • fibonacci(0)은 0을 출력하고, 0을 리턴한다.
  • fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
  • 첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
  • fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.

1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때, fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다.

각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. N은 40보다 작거나 같은 자연수 또는 0이다.

출력

각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.

작성한 코드

let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().split("\n");

let T = Number(input[0]); // 테스트 케이스 개수

// DP 테이블 초기화
let dp = new Array(41).fill(0);
dp[0] = 0;
dp[1] = 1;

// DP 테이블 채우기(피보나치 수열) -> 점화식 이용
for (let i = 2; i <= 40; i++) {
  dp[i] = dp[i - 1] + dp[i - 2];
}

for (let i = 1; i <= T; i++) {
  let n = Number(input[i]);
  if (n === 0) console.log(1, 0);
  else console.log(dp[n - 1], dp[n]);
}

풀이

  • 0의 개수는 해당 값의 바로 이전 값
  • 1의 개수는 현재 자신의 값

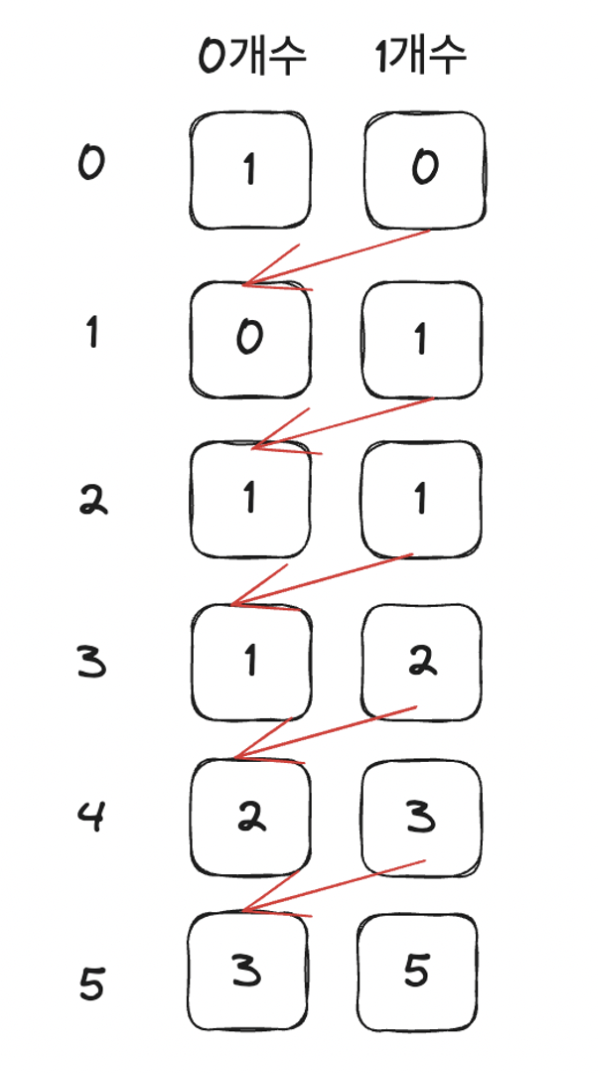
2. 01타일(1904)

문제

지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다.

어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진 00 타일들을 만들었다. 결국 현재 1 하나만으로 이루어진 타일 또는 0타일을 두 개 붙인 한 쌍의 00타일들만이 남게 되었다.

그러므로 지원이는 타일로 더 이상 크기가 N인 모든 2진 수열을 만들 수 없게 되었다. 예를 들어, N=1일 때 1만 만들 수 있고, N=2일 때는 00, 11을 만들 수 있다. (01, 10은 만들 수 없게 되었다.) 또한 N=4일 때는 0011, 0000, 1001, 1100, 1111 등 총 5개의 2진 수열을 만들 수 있다.

우리의 목표는 N이 주어졌을 때 지원이가 만들 수 있는 모든 가짓수를 세는 것이다. 단 타일들은 무한히 많은 것으로 가정하자.

입력

첫 번째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 1,000,000)

출력

첫 번째 줄에 지원이가 만들 수 있는 길이가 N인 모든 2진 수열의 개수를 15746으로 나눈 나머지를 출력한다.

작성한 코드

let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().split("\n");
let N = Number(input[0]);

// DP 테이블 초기화
let d = new Array(1000001).fill(0);
d[1] = 1;
d[2] = 2;

for (let i = 3; i <= N; i += 1) {
	// 값이 매우 커질 수 있으므로 나머지를 값에 넣기
  d[i] = (d[i - 1] + d[i - 2]) % 15746;
}

console.log(d[N]);

❗️값이 매우 커질 수 있음을 고려하기!!!

풀이

N=1일 때, 1 → 1가지

N=2일 때, 00, 11 → 2가지

N=3일 때, 001, 100, 111 → 3가지

N=4일 때, 0000, 0011, 1001, 1100, 1111 → 5가지

N=5일때, 00001, 00100, 10000, 00111, 10011, 11001, 11100, 11111 → 8가지

즉, 점화식은 ana_n = an−1a_{n-1}+an−2a_{n-2}

3. 포도주 시식(2156)

문제

효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다.

  1. 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
  2. 연속으로 놓여 있는 3잔을 모두 마실 수는 없다.

효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오.

예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.

입력

첫째 줄에 포도주 잔의 개수 n이 주어진다. (1 ≤ n ≤ 10,000) 둘째 줄부터 n+1번째 줄까지 포도주 잔에 들어있는 포도주의 양이 순서대로 주어진다. 포도주의 양은 1,000 이하의 음이 아닌 정수이다.

출력

첫째 줄에 최대로 마실 수 있는 포도주의 양을 출력한다.

작성한 코드

let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().split("\n");

let n = Number(input[0]); // 포도주 잔의 개수
let arr = [];
for (let i = 1; i <= n; i++) {
  arr.push(Number(input[i]));
}

// DP 테이블 초기화
let dp = new Array(n).fill(0);
dp[0] = arr[0];
dp[1] = arr[0] + arr[1];
dp[2] = Math.max(arr[0] + arr[1], arr[0] + arr[2], arr[1] + arr[2]);

// 점화식
for (let i = 3; i < n; i++) {
  dp[i] = dp[i - 1];
  dp[i] = Math.max(dp[i], arr[i] + dp[i - 2]);
  dp[i] = Math.max(dp[i], arr[i] + arr[i - 1] + dp[i - 3]);
}

console.log(dp[n - 1]);

풀이

  • 연속으로 마실 수 있는 잔은 최대 2잔

dp[i]: i번째 포도주까지의 최적의 해(최댓값)

최댓값 선택 → 나눠서 생각

  1. i번째 안 마시기: dp[i-1]

  2. i번째 마시고

    1) arr[i]+dp[i-2] → i-1번째는 안마시기

    2) arr[i]+arr[i-1]+dp[i-3] → i-1번째 마시기(i-2번째는 마실 수 없음)

4. 파도반 수열(9461)

문제

오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.

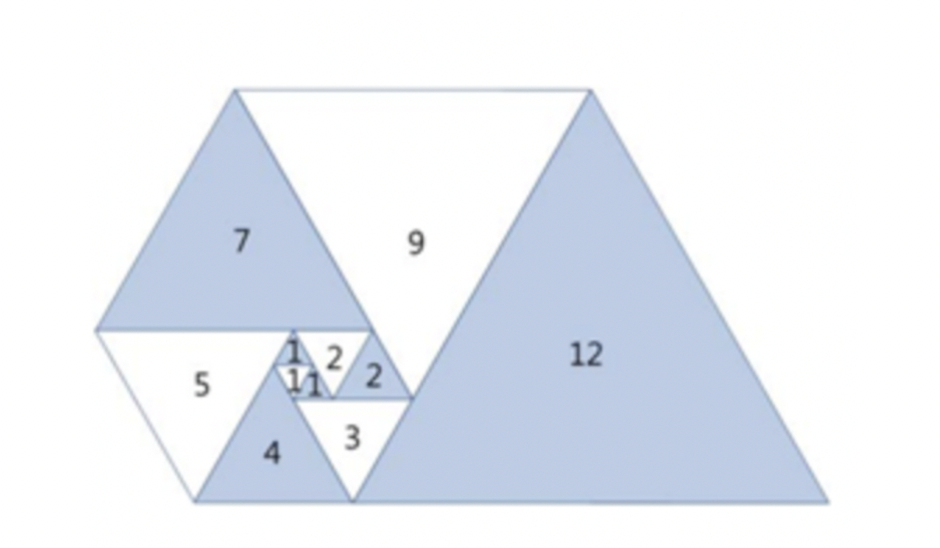
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.

N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)

출력

각 테스트 케이스마다 P(N)을 출력한다.

작성한 코드

let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().split("\n");

let T = Number(input[0]);

let dp = new Array(101).fill(0);
dp[0] = 0;
dp[1] = 1;
dp[2] = 1;

for (let i = 3; i <= 100; i++) {
  dp[i] = dp[i - 2] + dp[i - 3];
}

for (let i = 1; i <= T; i++) {
  let N = Number(input[i]);
  console.log(dp[N]);
}

풀이

N=1일 때, 1

N=2일 때, 1

N=3일 때, 1

N=4일 때, 2

N=5일 때, 2

N=6일 때, 3

N=7일 때, 4

N=8일 때, 5

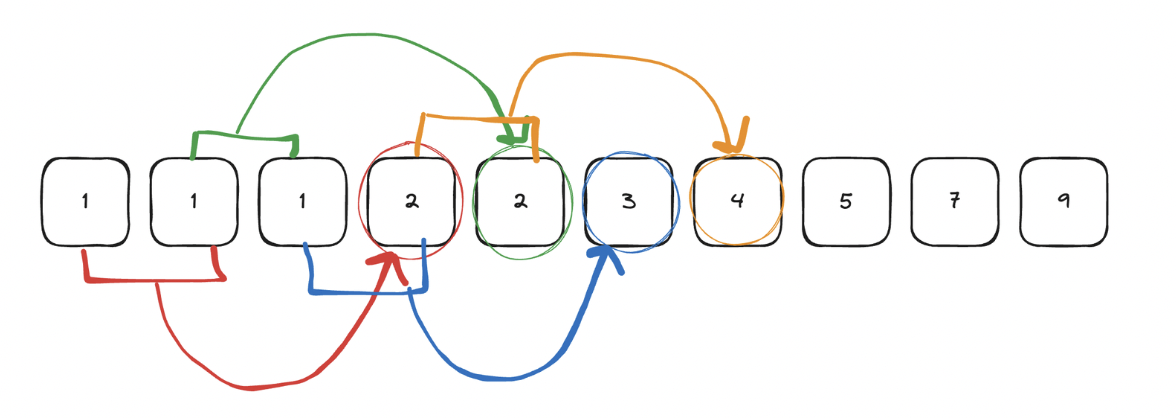
즉, 점화식은 ana_n = an−1a_{n-1}+an−2a_{n-2}

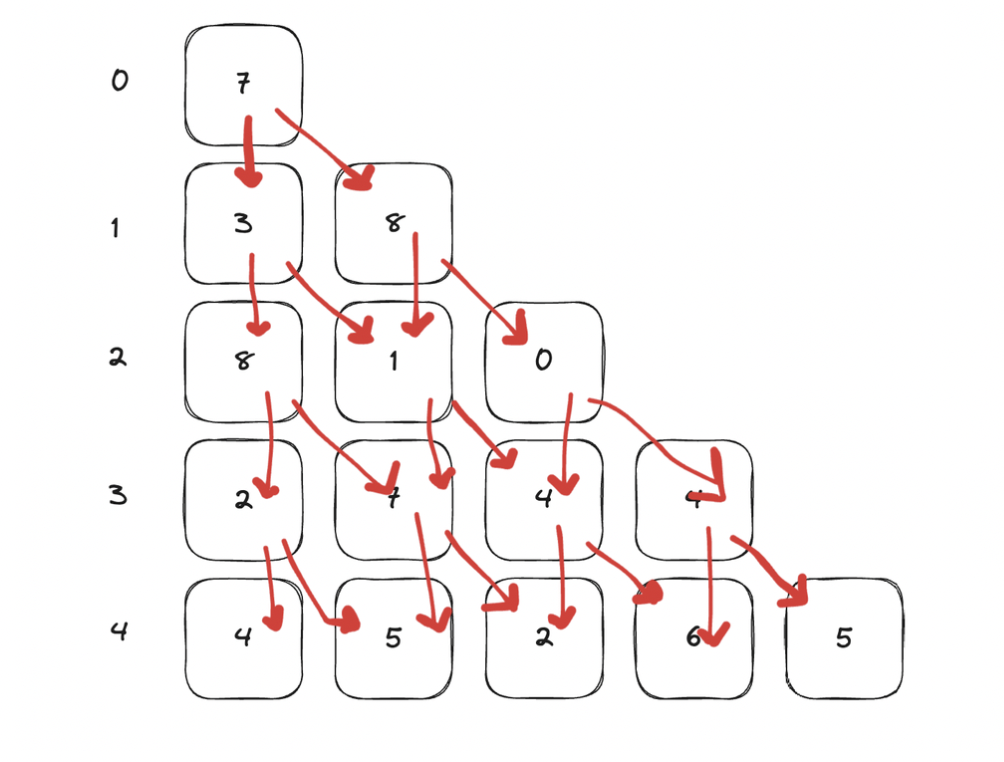
5. 정수 삼각형(1932)⭐️

문제

        7
      3   8
    8   1   0
  2   7   4   4
4   5   2   6   5

위 그림은 크기가 5인 정수 삼각형의 한 모습이다.

맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.

삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.

입력

첫째 줄에 삼각형의 크기 n(1 ≤ n ≤ 500)이 주어지고, 둘째 줄부터 n+1번째 줄까지 정수 삼각형이 주어진다.

출력

첫째 줄에 합이 최대가 되는 경로에 있는 수의 합을 출력한다.

작성한 코드

let fs = require("fs");
let input = fs.readFileSync("/dev/stdin").toString().split("\n");

let n = Number(input[0]); // 삼각형의 크기
let dp = []; // DP 테이블 초기화

for (let i = 1; i <= n; i++) {
  let data = input[i].split(" ").map(Number);
  dp.push(data);
}

// DP로 2번째 줄부터 내려가며 확인
for (let i = 1; i < n; i++) {
  for (let j = 0; j <= i; j++) {
    // 왼쪽 위에서 내려오는 경우
    let upLeft = 0;
    if (j !== 0) upLeft = dp[i - 1][j - 1];
    // 바로 위에서 내려오는 경우
    let up = 0;
    if (j !== i) up = dp[i - 1][j];
    // 최대 합 저장
    dp[i][j] = dp[i][j] + Math.max(upLeft, up);
  }
}
console.log(Math.max(...dp[n - 1]));

풀이

특정한 위치에 도달하기 위해서는 2가지 위치에서만 내려올 수 있음

1) 왼쪽 위 2) 바로 위

dp[i][j] = arr[i][j]+max(dp[i-1][j-1], dp[i-1][j])

❗️ 리스트 범위 벗어나지 않게 주의!

profile
Minji Lee
이전 포스트

정렬(Sorting) 알고리즘 문제풀이

다음 포스트

DFS 알고리즘(깊이 우선 탐색)

0개의 댓글