집합 커버 문제 개요
- n개의 원소를 가진 집합인 U가 있고, U의 부분 집합들을 원소로 하는 집합 F가 주어질 때, 어떤 집합들을 선택하여 합집합이면 U와 같게되는 최소의 집합 수로 결정하는 문제
문제 예시
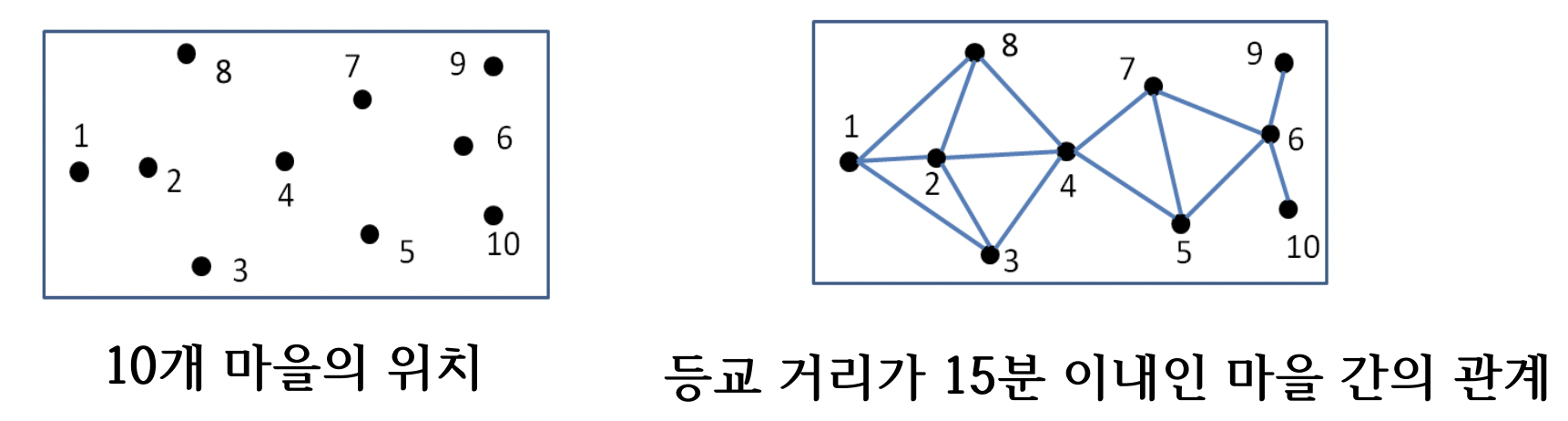
- 만약 신도시를 계획하는데 각 도시를 커버할 수 있는 최소한의 학교를 건설하는 문제를 가질 때 해결 할 수 있는 방법은 여러가지가 있다.
단순한 해결 방법
- 단순한 해결 방법은 모든 경우의 수를 전부 대입하여 풀어보는 브루트 포스 문제
- 해당 방법은 매우 오래걸리는 방법이며, O(2n)이 소요될 수 있다.
- 위의 예제에서는 O(210)이 소요 될 수 있는 상황
- 해당 문제를 극복하기 위해 최적해를 찾는 방법을 이용한다.
효율적인 해결 방법
- 최적해를 가진 근사해를 이용하여 문제를 해결한다.
Peseudo Code
setCover
입력: U,F={S_i}, i= 1,...,n
출력: 집합 커버 C
C= null
while (U=null) do {
U의 원소를 가장 많이 가진 U_i를 선택
U = U - S_i
S_i를 F에서 제거하고, S_i를 C에 추가
return C
수행 과정

- 위의 집합이 있을 때, 가장 큰 부분집합 부터 차례대로 U를 제거
시간 복잡도
- while 루프가 수행되는 횟수는 최대 n회
- 루프가 1회 수행될 때마다 집합 U의 원소가 1개씩만 커버된다면, 최악의 경우 루프가 n번 수행
- 루프가 1회 수행 될 때
- U의 원소들을 가장 많이 포함하고 있는 집합 S를 찾으려면, 현재 남아있는 S_i들 각각을 U와 비교하여야한다.
- S_i들의 수가 최대 n이라면 각 S_i와 U의 비교는 O(n) 시간이 걸리므로 O(n2) 시간 소요
- 집합 U에서 집합 S_i의 원소를 제거하므로 O(n) 시간 소요
- S_i를 F에서 제거하고 C에 추가하는 시간 O(1) 시간
- 따라서 O(n3) 시간 소요



