산점도, 공분산, 상관계수, 검정
- 두 사건 간의 연관성을 분석하기 위해서
- 둘 이상의 변수들이 서로 관련성을 가지고 변화할 때 관계를 분석
- 상관분석, 회귀분석
ex) GDP와 기대수명 간의 관계, 키와 몸무게 간의 관계
여기선 당뇨와 그에 영향을 미치는 변수들 간의 관계를 분석
- Sklearn에서 제공하는 datasets를 불러옴
import pandas as pd
import numpy as np
from sklearn import datasets
data = datasets.load_diabetes()# 자동입력
%config Completer.use_jedi = Falsedata.keys()dict_keys(['data', 'target', 'frame', 'DESCR', 'feature_names', 'data_filename', 'target_filename', 'data_module'])data['data'].shape(442, 10)data['target'].shape(442,)len(data['feature_names'])10df = pd.DataFrame(data['data'], index=data['target'], columns=data['feature_names'])
df| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 151.0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 75.0 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 141.0 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 206.0 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 135.0 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 178.0 | 0.041708 | 0.050680 | 0.019662 | 0.059744 | -0.005697 | -0.002566 | -0.028674 | -0.002592 | 0.031193 | 0.007207 |
| 104.0 | -0.005515 | 0.050680 | -0.015906 | -0.067642 | 0.049341 | 0.079165 | -0.028674 | 0.034309 | -0.018118 | 0.044485 |
| 132.0 | 0.041708 | 0.050680 | -0.015906 | 0.017282 | -0.037344 | -0.013840 | -0.024993 | -0.011080 | -0.046879 | 0.015491 |
| 220.0 | -0.045472 | -0.044642 | 0.039062 | 0.001215 | 0.016318 | 0.015283 | -0.028674 | 0.026560 | 0.044528 | -0.025930 |
| 57.0 | -0.045472 | -0.044642 | -0.073030 | -0.081414 | 0.083740 | 0.027809 | 0.173816 | -0.039493 | -0.004220 | 0.003064 |
442 rows × 10 columns
1. 산점도
- 직교 좌표계를 이용해 두 개 변수 간의 관계를 나타내는 방법
- 상관계수를 파악하기 전에 산점도를 그려서 두 변수 간에 관련성을 시각적으로 파악
# target(당뇨병의 수치), bmi(체질량지수)
# 두 변수는 서로 양의 관계를 나타냄
# Bmi가 증가할수록 Target도 증가함으로 양의 상관관계를 보임
x = df.bmi.values
y = df.index.values
import matplotlib.pyplot as plt
plt.scatter(x, y, alpha=0.5)
plt.title('TARGET ~ BMI')
plt.xlabel('BMI')
plt.ylabel('TARGET')
plt.show()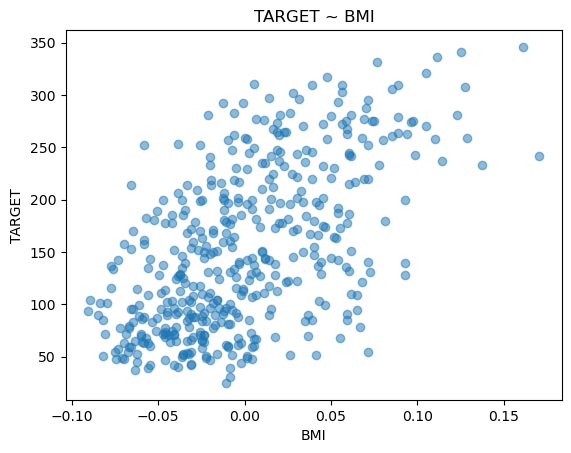
- 산점도를 이용하면 두 변수 간의 직선적인 관계를 대략적으로 표현
- 두 변수 사이의 관계를 어떠한 수치로 표현하지는 못함
- 따라서 두 변수 간의 관계를 수치로 표현하기 위해서 공분산 및 상관계수를 이용
- 공분산(Covariance) 및 상관계수(Correlation Coefficient)
- 공분산
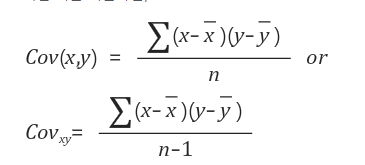
cov = (np.sum(x*y) - len(x)*np.mean(x)*np.me
2.1480435755297007
```python
# numpy를 이용하면 쉽게 이용 cov()
np.cov(x,y)[0,1]2.1529144226397467위와 같이 공분산은 상관관계의 상승 혹은 하강하는 경향을 이해할 순 있으나 2개 변수의 측정 단위의 크기에 따라 값이 달라지므로 절대적 강도를 파악하기에는 한계
- 따라서 공분산을 표준화 시킨 상관계수를 보다 많이 이용
- 각 변수의 표준편차를 분모로 나눔
corr = cov / (np.std(x) * np.std(y))
corr0.5864501344746884numpy corrcoef를 이용
# 상관계수는 -1에서 1 사이의 값을 가지기에 0일 경우에는 두 변수 간의 선형관계가 전혀 없다.
# 0.3과 0.7 사이이면, 뚜렷한 양적 선형관계로 0.7과 1.0 사이는 강한 양적 선형관계로 간주
# 주의할 내용은 상관계수 분석 자체가 특이 값에 민감하게 반응하기 때문에 데이터 pre-processing에 항상 주의를 기울여야함
# 상관관계는 두 변수 간의 관련성을 의미할 뿐, 원인과 결과의 방향을 알려주진 않음
np.corrcoef(x,y)[0,1]0.5864501344746886- 상관계수의 검정
- 상관계수 값 자체가 유의미한가를 검정
- p-value를 많이 이용
- scipy 패키지의 stats.pearsonr()을 이용하면 상관계수와 p-value를 동시에 얻음
# 뒤 결과 값이 p-value인데, 귀무가설 "상관관계가 없다"에 대한 검정 결과 p-value가 3.4~~라는 0에 아주 매우 가까운 값이 나왔으므로
# 귀무가설을 기각할 수 있음을 알 수 있다.
import scipy.stats as stats
stats.pearsonr(x,y)PearsonRResult(statistic=0.5864501344746886, pvalue=3.4660064451655095e-42)통계학에서 , 피어슨 상관 계수(Pearson Correlation Coefficient ,PCC)란 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치다. 피어슨 상관 계수는 코시-슈바르츠 부등식에 의해 +1과 -1 사이의 값을 가지며, +1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다. 일반적으로 상관관계는 피어슨 상관관계를 의미하는 상관계수이다.
# 나머지 변수들도 상관계수를 확인
# 당뇨병수치와 상관관계가 가장 높은것은 bmi이고 age나 sex는 큰 관련이 없음
for item in ['age', 'sex', 'bmi', 'bp']:
print(item)
x = df[item].values
print('Covariance: {:.2f}'.format(np.cov(x,y)[0,1]))
print('Correlation: {:.2f}'.format(stats.pearsonr(x,y)[0]))
print('P-value: {:.4f}'.format(stats.pearsonr(x,y)[1]))
print('\n')age
Covariance: 0.69
Correlation: 0.19
P-value: 0.0001
sex
Covariance: 0.16
Correlation: 0.04
P-value: 0.3664
bmi
Covariance: 2.15
Correlation: 0.59
P-value: 0.0000
bp
Covariance: 1.62
Correlation: 0.44
P-value: 0.0000