백준 6588, 1676, 2004 문제 풀이

1.오늘의 알고리즘 문제

• 1. 골드바흐의 추측
     

public class p6588 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();

        final int MAX_NUM = 1000000;


        boolean[] check = new boolean[MAX_NUM + 1];
        Arrays.fill(check, false);   // true면 지워진거고 false면 안지워진것
        check[0] = true;   // 0은 소수가 아님
        check[1] = true;   // 1은 소수가 아님

        for (int i = 2; i <= MAX_NUM; i++) {
            if (check[i] == false) {
                for (int j = i * 2; j <= MAX_NUM; j += i) {
                    check[j] = true;
                }
            }
        }

        int n = Integer.parseInt(br.readLine());
        while (n != 0) {
            boolean result = false;
            for(int i=n-1; i>=3; i--){
                if(check[i] == false && check[n-i] == false){
                    sb.append(n + " = " + (n-i) + " + " + i + "\n");
                    result = true;
                    break;
                }
            }
            if(result == false) {
                sb.append("Goldbach's conjecture is wrong.");
            }
            n = Integer.parseInt(br.readLine());
        }

        System.out.println(sb);
    }
}


//분류 : 골드 바흐의 추측(수학)
//알고리즘 : 골드 바흐의 추측이 무엇이냐면 "4보다 큰 모든 짝수는 두 홀수 소수의 합으로 나타낼 수 있다." 이다. 예를 들어 8은 3 + 5로 나타낼 수 있고,
//3 과 5는 모두 홀수인 소수이다. 또, 20 = 3 + 17 = 7 + 13, 42 = 5 + 37 = 11 + 31 = 13 + 29 = 19 + 23 이다.
//따라서 풀이 방법은 에라토스테네스의 체를 사용하여 소수들만 남긴 배열을 만들어 준 뒤, n = i + (n-i) 이기 때문에 check[i] 도 false 이고 check[n-i] 도 false
//이면 두개의 소수의 합으로 나타낼 수 있다.
//배운점: Arrays.fill 사용하는게 익숙해졌고, 에라토스테네스의 체 알고리즘을 정확히 숙지한 것 같다.또한 자바 상수 final을 사용해 보는 문제가 되었다.

• 2. 팩토리얼의 0의 개수 세기
     

public class p1676 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());

        //5의 개수만 가지고 판별

        int n1 = n/5; //인수로 5를 하나가지고 있는 n까지의 수
        int n2 = n/25; //인수로 5를 2개 가지고 있는 n까지의 수
        int n3 = n/125; //인수로 5를 3개 가지고 있는 n까지의 수

        System.out.println(n1+n2+n3);

    }
}

//분류 : 팩토리얼의 0의 개수 세기(수학)
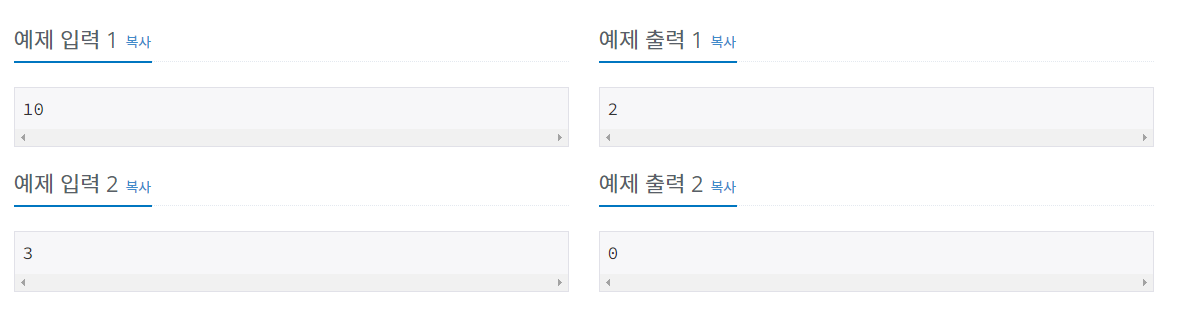
//문제 : N!에서 뒤에서부터 처음 0이 아닌 숫자가 나올 때까지 0의 개수를 구하는 프로그램을 작성하시오.
//알고리즘 : 팩토리얼은 1x2x3x4x5x6.... 을 하는것인데 이것을 계산해서 0의 개수를 구하기란 쉽지않다. 따라서 0이 나올때의 특징을 파악해야하는데 0이 나오기 위해서는
// 소인수 분해를 하였을때 (2x5)가 몇번 나올지 파악하면 된다. 추가적으로 2의 개수는 항상 5의 개수보다 많으므로 인수로 5의 개수가 몇개있는지만 파악해주면 풀 수 있다.
//배운점: 팩토리얼을 구현하여 풀줄만 알지 사실 이런 응용문제를 해결하기 위해서는 어느정도 선행 지식이 필요하다고 느껴졌다.과연 문제로 나왔을때 선행 지식 없이 풀수있을까?
//의문이드는 간단해보이지만 어려운 문제였다.

• 3. 조합 0의 개수
     
     

public class p2004 {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());

        int twoCnt = getCount(n, 2) - getCount(m, 2) - getCount(n - m, 2);
        int fiveCnt = getCount(n, 5) - getCount(m, 5) - getCount(n - m, 5);

        System.out.println(Math.min(twoCnt,fiveCnt));

    }


    public static int getCount(int n, int k) {
        int cnt = 0;

        while (n >= k) {
            cnt += n / k;
            n /= k;
        }

        return cnt;
    }
}


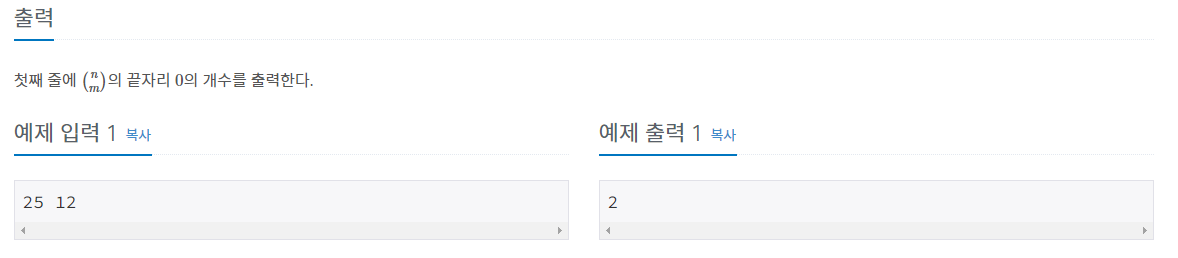
//분류 : 조합 0의 개수(수학)
//알고리즘 : 조합에서는 팩토리얼 0의 개수와 비슷하지만 2의 개수가 5의 개수보다 적은 경우가 존재하기 때문에 2의 개수일때와 5의 개수를 따로 계산하여 더 작은
//수를 출력해 준다.
//배운점 : 이 문제를 풀면서 runtime 에러 /By zero가 엄청 많이 나왔다 왜 나왔을까 의심되는 부분은 처음에 문제를 풀때 k를 제곱해서 n/k 를 계산하는 방법으로
//했지만 int 의 범위가 늘어나는 k의 값이 발생하여 / By zero가 나온것 같다. 그래서 해결하기위해 n을 k로 계속해서 나눠주는 방식으로 바꿔서 해결하게 되었다.