해 탐색 알고리즘
- 백트래킹 기법
- 분기 한정 기법
- 유전자 알고리즘
- 모의 담금질 기법
🟩 백트래킹(Backtracking) 기법
해를 찾는 도중에 '막히면' (즉, 해가 아니면) 되돌아가 다시 해를 찾아가는 기법
- 최적화(optimization) 문제 - NP
- 결정(decision) 문제 - yes/no
를 해결할 수 있다!
DFS(깊이 우선 탐색)을 기반으로 하며 경우의 수를 탐색하여 내려가다가 해당 노드가 조건에 맞지 않는다고 생각 되면 가지치기 한다.
🟣 TSP에서의 백트래킹 알고리즘
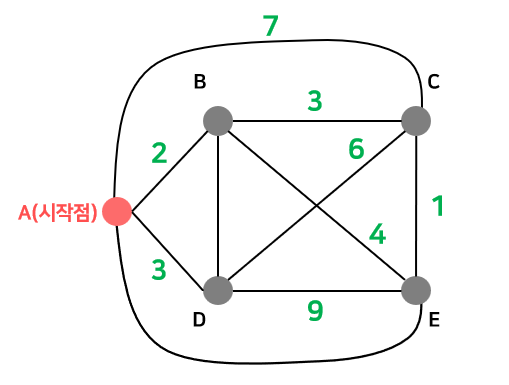
⬜ TSP(Traveling Salesman Problem)
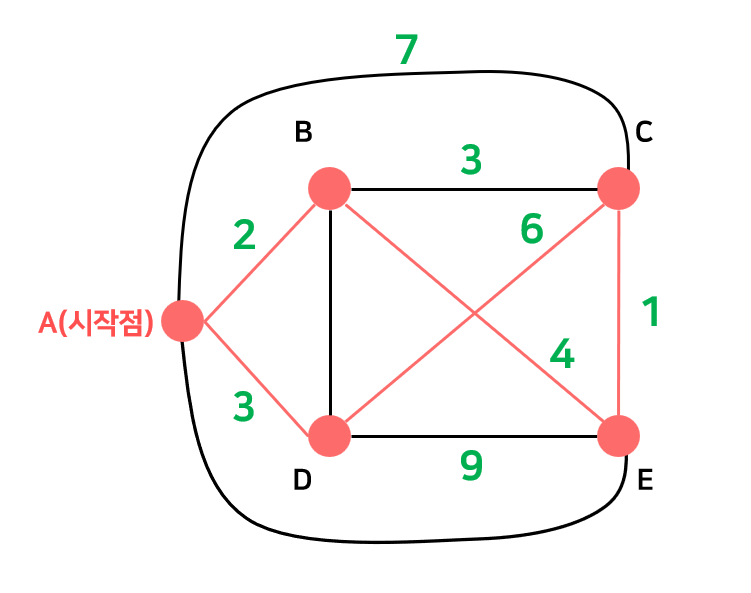
주어진 n개의 지점을 연결하는 최소 비용 경로를 찾는 문제
└▷ 여러 도시들이 있고 한 도시에서 다른 도시로 이동하는 비용이 모두 주어졌을 때, 모든 도시들을 단 한 번만 방문하고 원래 시작점으로 돌아오는 최소 비용의 이동 순서를 구하는 것이다.
⬜ 알고리즘
tour = [시작점] // 방문한 점의 순서 (root node)
bestSolution = (tour, ∞)
// └▷ ∞ : 방문 거리(최소값을 찾기 위해 일단 최대값으로 초기화)
// └▷ bestSolution 은 현재까지 찾은 방문지(해) 중 거리가 가장 짧은 해
// └▷ tour는 점의 순서, tour의 거리는 'bestSolution의 거리'
BacktrackTSP(tour)
1. if(tour가 완전한 해이면) // A에서 출발해 A로 도착하면
2. if(tour의 거리 < bestSolution의 거리)
3. bestSolution = (tour, tour의 거리)
4. else // 자식(인접) 노드를 찾아 깊게 들어간다(재귀호출)
5. for(tour를 확장 가능한 점 v에 대해서)
6. newTour = tour+v // 기존 tour의 뒤에 방문하지 않은 인접 노드 v를 추가
7. if(newTour의 거리 < bestSolution의 거리) // 가지치기
8. BacktrackTSP(newTour)⬜ 예시 (알고리즘 수행 과정)
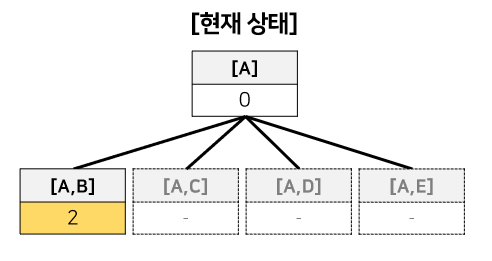
tour = [A]ㅤbestSolution([A], ∞)
#1 - BacktrackTSP([A]) 호출

- tour가 완전한 해가 아니므로 if문 건너뛰기.
- else문 진입
- tour를 확장 가능한 점 v에 대해서 for문을 순회
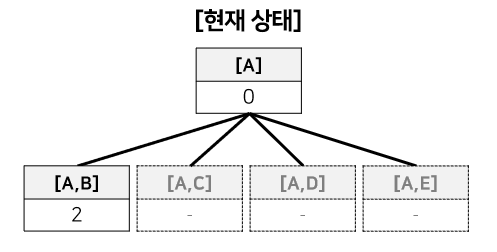
- newTour = [A,B]
- newTour 거리(==2) < bestSolution 거리(==∞) 이므로
- Backtrack(newTour) 재귀함수 호출
#2 - BacktrackTSP([A, B]) 진입
- tour가 완전한 해가 아니므로 if문 건너뛰기.
- else문 진입
- tour를 확장 가능한 점 v에 대해서 for문 순회
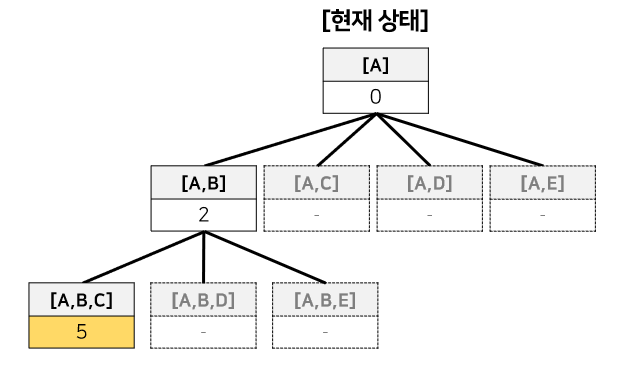
- newTour = [A,B,C]
- newTour 거리(==5) < bestSolution 거리(==∞) 이므로
- Backtrack(newTour) 재귀함수 호출
같은 방식으로 #3 단계 생략…
#4 - BacktrackTSP([A, B, C, D, E, A]) 진입
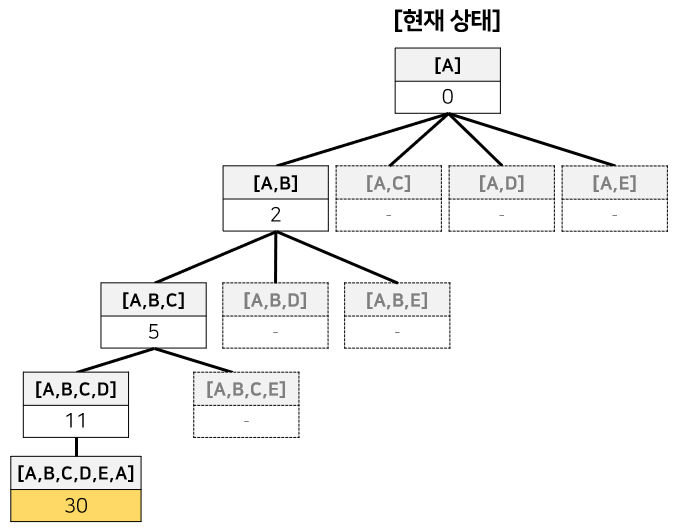
- tour가 완전한 해(A에서 출발해서 A로 도착) 이므로 if문 진입
- tour의 거리(==30) < bestSolution(==∞) 이므로
- bestSolution = [[A,B,C,D,E,A], 30]
- 함수 종료, #4를 호출한 #3으로 돌아감.
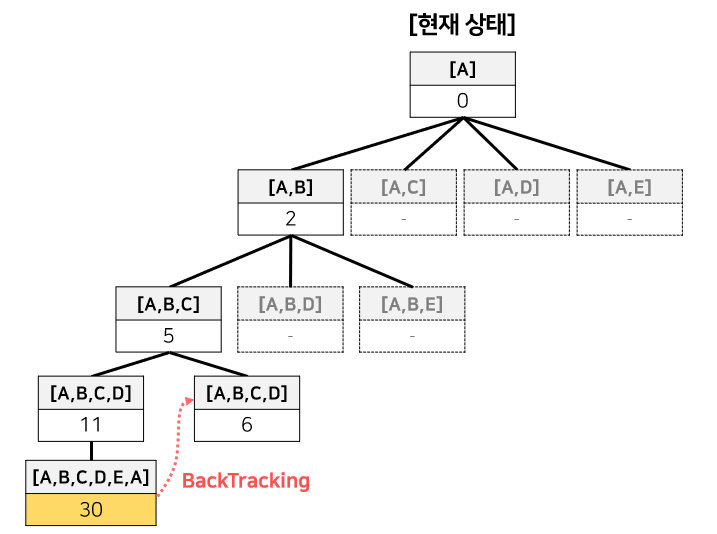
#3으로 돌아와 - 두 번째 for문을 돌고 newTour=[A,B,C,D] → Backtrack(newTour)호출
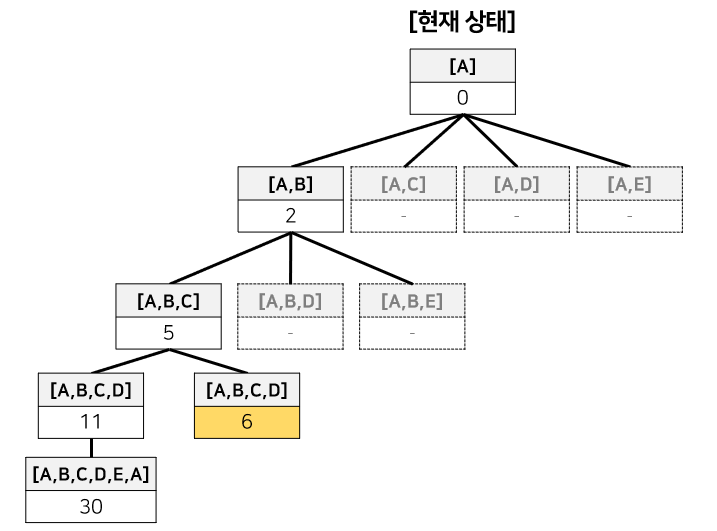
같은 방식으로 두 번째 완전한 해를 찾으면 아래와 같다.
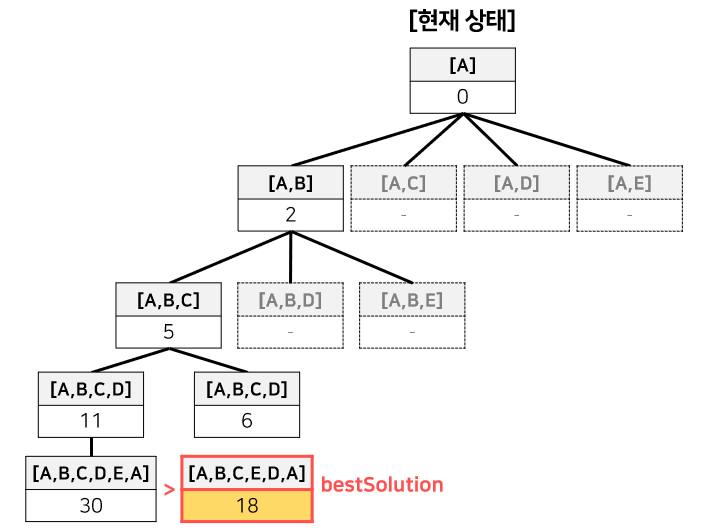
2번째 완전한 해가 앞서 찾은 bestSolution 보다 작으므로 bestSolution이 교체 된다.
#2으로 돌아와 - 두 번째 for문을 돌고 newTour=[A,B,D] → Backtrack(newTour)호출
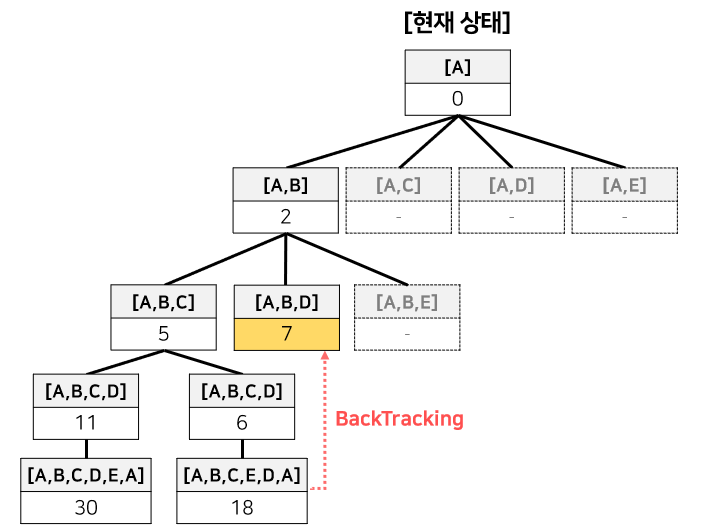
이하동문으로 쭉쭉 완전한 해를 찾아 나서고, 백트래킹 하고, 나서길 반복하면...
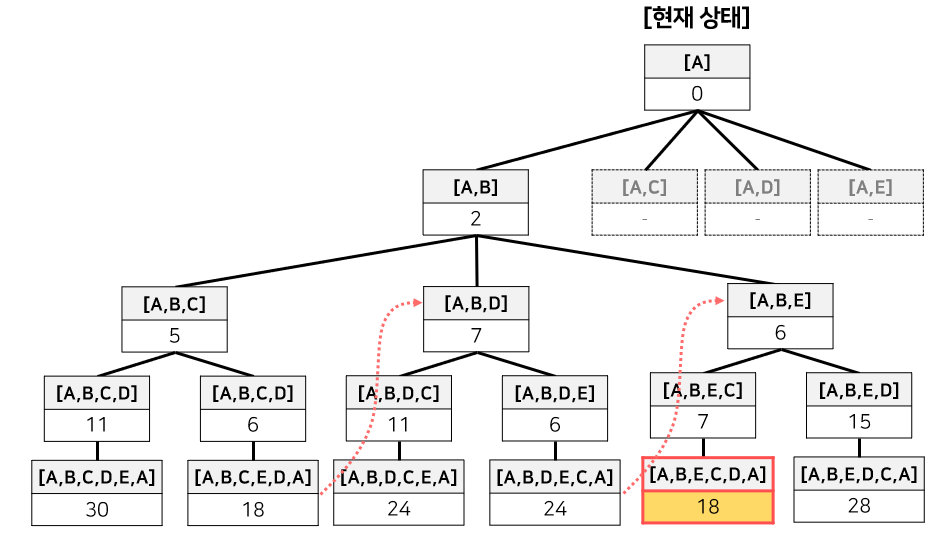
이렇게 tour=[A, B] 에 대한 모든 수행을 마친 결과가 나타난다.
bestSolution=([A,B,E,C,D,A], 16) 이 된다.
마찬가지로 tour=[A,C]에 대한 결과
지금부터 신기한 일이 발생한다.
완전한 해를 구하기도 전에 bestSolution 보다 큰 경로를 얻게 되고, 그렇다는 말은 즉 더이상 해를 탐색하지 않고 다음 해로 넘어가도 된다는 뜻이다.
이걸 가지치기(pruning)라고 한다.
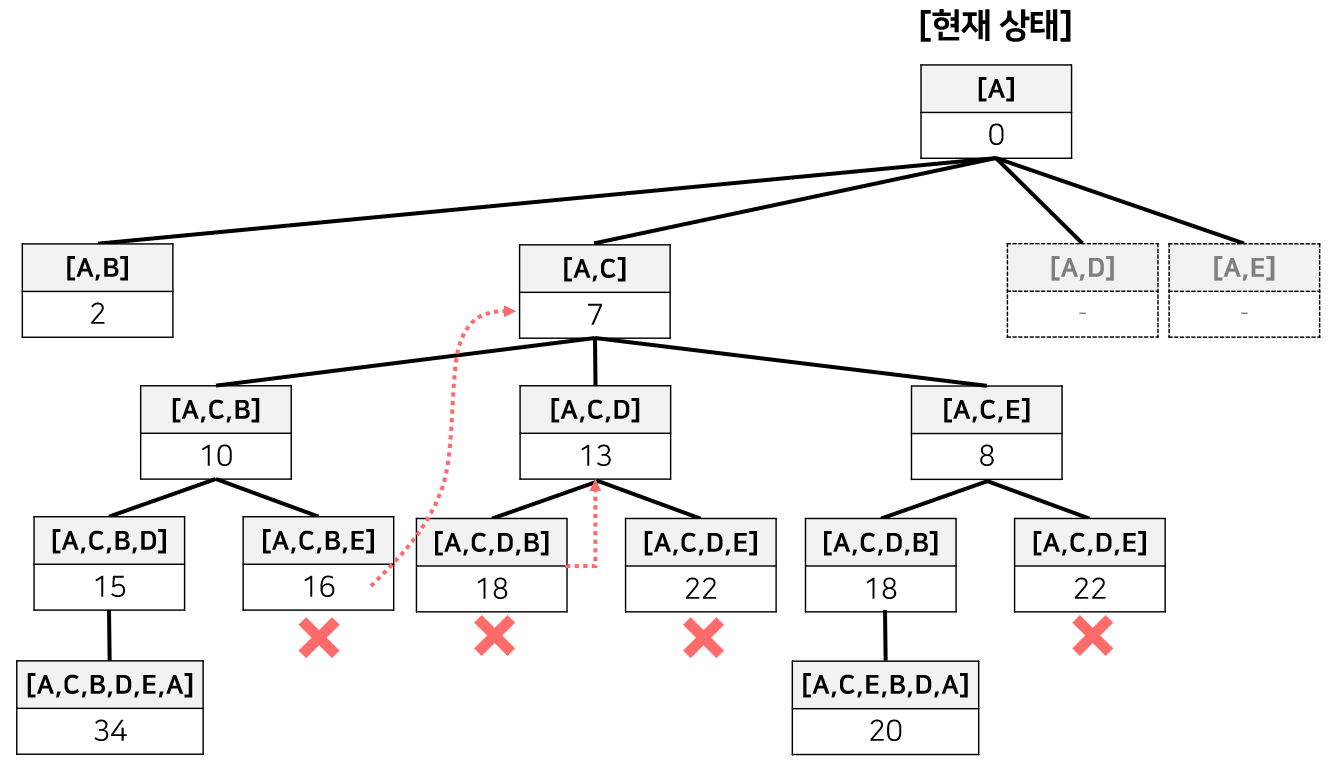
이를 토대로 tour=[A,E]까지 탐색하면
최종해 = [A, B, E, C, D, A] 거리 = 16
이 된다!!
⬜ 시간복잡도
Backtracking 알고리즘의 시간 복잡도는 상태 공간 트리의 노드 수에 비례한다.
└▶ n개의 점이 있는 입력 그래프에 대해서 BacktrackTSP 알고리즘이 탐색하는 최대 크기의 상태 공간 트리
ㅤㅤ(root)
ㅤㅤ 1개
ㅤㅤㅤ|
ㅤㅤ(n-1) 개 : 시작점 빼고 방문
ㅤㅤㅤ|
ㅤ(n-1)(n-2) 개 : 부모+시작점 빼고 방문
ㅤㅤㅤ|
ㅤ(n-1)(n-2)(n-3) 개
ㅤㅤㅤ.
ㅤㅤㅤ.
ㅤㅤㅤ.
(n-1)(n-2)(n-3)…2*1 개 = leaf 개수
= 트리의 이파리 노드 수만 계산해도 (n-1)!
최악의 경우 가지치기를 하나도 못 하게 되고 2^n 개의 노드를 대부분 탐색해야 하므로 지수 시간이 걸린다.
이는 모든 경우를 다 검사하여 해를 찾는 완전 탐색(Exhaustive Search)의 시간 복잡도와 같다.
그러나 일반적으로 백트래킹 기법은 가지치기를 하기 때문에 완전 탐색보다 훨씬 효율적이다.

