[Python]백준_25373 : 벼락치기

Alal11·2022년 12월 25일

출처

https://www.acmicpc.net/problem/25373

문제

부산사이버대학교에 다니는 대희는 강의 영상 보는 것을 매일 미뤘다. 오늘은 중간고사가 일주일 남은 날이다. 대희는 더 이상 미루면 큰일이 날 것 같아서 오늘부터 밀린 영상을 보기로 했다. 그런데 아직 정신을 못 차린 대희는 영상을 본 다음 날은 그 전날보다 영상을 적게 본다. 이때 영상을 모두 듣기 위해 첫날 들어야 하는 영상의 개수 중 가장 작은 값을 출력하자.

영상을 하나도 보지 않은 날부터는 계속 영상을 보지 않는 것에 유의하자.

입력

밀린 영상 개수 $N$ 이 주어진다.

출력

첫날 봐야 하는 영상의 개수 중 가장 작은 값을 출력한다.

제한

$1 \leq N \leq 10^{17}$

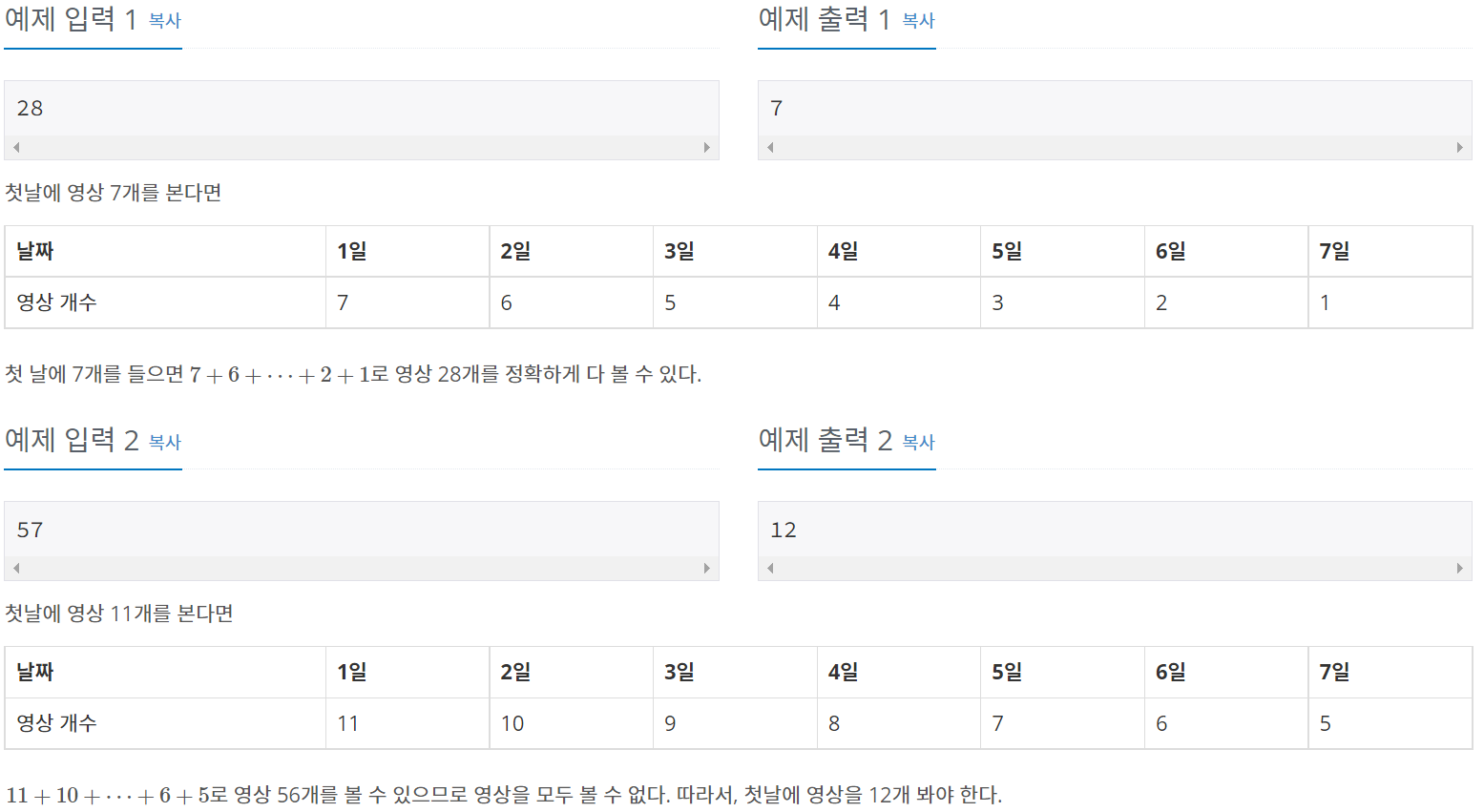
예제 입출력

알고리즘 분류

수학
많은 조건 분기

➡️문제 분석

일주일 안에 n개의 영상을 모두 봐야 한다.
전날은 항상 다음날보다 영상을 적게 본다.
첫날 들어야 하는 영상 개수의 최솟값을 출력한다.

7+6+...+1 = 28을 기준으로 나눈다.

n이 28보다 작은 경우

n=1이면
1

n=2이면
2

n=3이면
2 1

n=4이면
3 1

n=5이면
3 2

n=6이면
3 2 1

n=7이면
4 3 또는 4 2 1

n=8이면
4 3 1

n=9이면
4 3 2

n=10이면
4 3 2 1

n=11이면
5 4 2

…

n=15이면
5 4 3 2 1

…

n=21이면
6 5 4 3 2 1

…

n=28이면
7 6 5 4 3 2 1

즉, 반복문으로 1부터 7까지 계속 더해주면서 크기를 비교해주는데

k+(k-1)+(k-2)+…+1 < n ≤ (k+1)+k+(k-1)+…+1 이라면 첫날 들어야 되는 영상 개수의 최솟값은 k+1이다.

예를 들어, n=8이면 3+2+1보다는 크고 4+3+2+1보다는 작다. 따라서 이때의 정답은 4가 된다.

n이 28보다 큰 경우

n이

29(8+6+5+4+3+2+1)에서 35(8+7+6+5+4+3+2) 사이 → 8

36(9+7+6+5+4+3+2)에서 42(9+8+7+6+5+4+3) 사이 → 9

43(10+8+7+6+5+4+3)에서 49(10+9+8+7+6+5+4) 사이 → 10

…

즉, 7을 주기로 영상의 개수가 1씩 증가한다.

이제 규칙을 찾아보자.

(n-29)이
0~6 사이 → 8
7~13 사이 → 9
14~20 사이 → 10

…

(n-29)을 7로 나눈 몫이
0이면 → 8
1이면 → 9
2이면 → 10

…

따라서 (n-29)을 7로 나눈 몫 + 8을 해주면
n이 28보다 큰 경우에 첫날 들어야 하는 최소의 영상 개수를 구할 수 있다.

➡️코드(⭕)

n = int(input())

if n <= 28:
    for i in range(1, 8):
        if n <= sum(range(1, i+1)):
            print(i)
            break

else:
    print((n-29)//7+8)