출처
https://www.acmicpc.net/problem/13301
문제
대구 달성공원에 놀러 온 지수는 최근에 새로 만든 타일 장식물을 보게 되었다. 타일 장식물은 정사각형 타일을 붙여 만든 형태였는데, 한 변이 1인 정사각형 타일부터 시작하여 마치 앵무조개의 나선 모양처럼 점점 큰 타일을 붙인 형태였다. 타일 장식물의 일부를 그리면 다음과 같다.
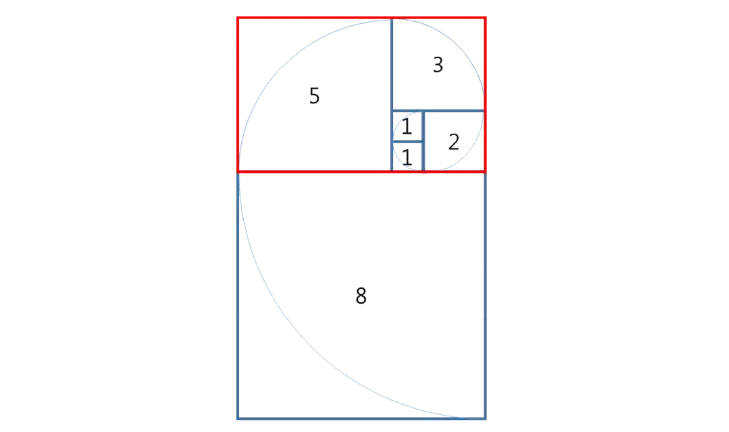
그림에서 타일에 적힌 수는 각 타일의 한 변의 길이를 나타낸다. 타일 장식물을 구성하는 정사각형 타일 한 변의 길이를 안쪽 타일부터 시작하여 차례로 적으면 다음과 같다.
1, 1, 2, 3, 5, 8, ...
지수는 문득 이러한 타일들로 구성되는 큰 직사각형의 둘레가 궁금해졌다. 예를 들어, 처음 다섯개의 타일이 구성하는 직사각형(위에서 빨간색으로 표시한 직사각형)의 둘레는 26이다.
타일의 개수 N(1 ≤ N ≤ 80)이 주어졌을 때, N개의 타일로 구성된 직사각형의 둘레를 구하는 프로그램을 작성하시오.
입력
표준 입력으로 다음 정보가 주어진다. 입력은 한 줄로 구성되며 이 줄에는 타일의 개수를 나타내는 정수 N(1 ≤ N ≤ 80)이 주어진다.
출력
표준 출력으로 N 개의 타일이 구성하는 타일 장식물 직사각형의 둘레를 출력한다.
64비트 정수형인 “long long” 자료형을 써야할 수 있음
서브태스크

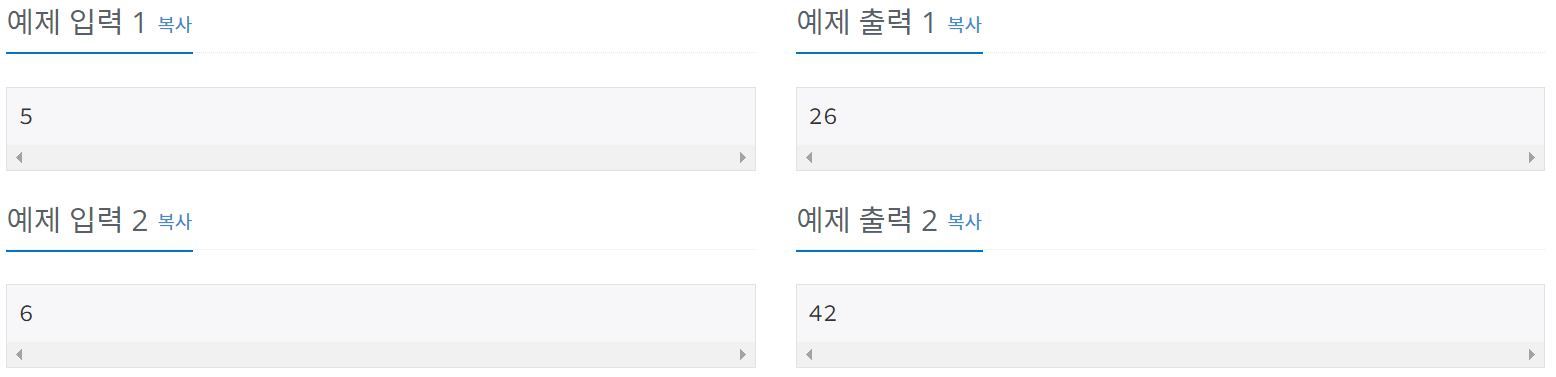
예제 입출력
알고리즘 분류
- 수학
- 다이나믹 프로그래밍
➡️문제 분석
직사각형 둘레의 길이의 합은 바로 직전의 정사각형 둘레와 전전의 정사각형 둘레의 합과 같다. 따라서 타일이 1개와 2개인 경우에만 따로 둘레 길이를 4와 6으로 설정해주고 이후부턴 전과 전전의 합으로 둘레의 길이를 구할 수 있다.
➡️코드(⭕)
n = int(input())
d = [0]*81 # d의 81개의 요소를 전부 0으로 채움
d[0] = 4
d[1] = 6
for i in range(2, n+1):
d[i] = d[i-1]+d[i-2] # 전과 전전 직사각형의 둘레 길이 합
print(d[n-1])
➡️코드 분석
-
타일의 개수 n을 입력받는다.
-
둘레의 길이를 담을 리스트 d의 81개의 요소를 전부 0으로 채운다. (81개인 이유는 타일의 개수 n의 최대가 80이기 때문에)
-
d의 인덱스 0과 1인(직사각형 개수가 1개와 2개) 경우는 따로 예외처리를 해줘서 4와 6 값을 직접 넣어준다.
-
반복문으로 i에 인덱스 2부터 n까지 반복해준다.
-
i번째 타일의 둘레 길이는 i-1번째와 i-2번째 타일의 둘레 길이를 합한 것과 같다.
-
d의 인덱스는 0부터, n은 1부터 시작이므로 d[n-1] 값을 출력한다.
➡️end
규칙을 찾아서 푸는 좋은 문제였다!