강화학습 논문 리뷰 CQL (Conservative Q-Learning for Offline Reinforcement Learning)

이 글은 논문 Conservative Q-Learning for Offline Reinforcement Learning에 대한 설명입니다. 논문 원본에 대한 링크는 아래에 적어놓았습니다.

1. 논문 원본 : https://arxiv.org/abs/2006.04779
2. 깃헙 링크 : https://github.com/aviralkumar2907/CQL

Abstract

• Challenge : 데이터셋(Transitions : State, Action, Next_State, Reward)을 수집하는 것
• 실제 환경에 강화학습을 적용하기 위해서는, 실제 환경에서 수많은 데이터를 수집해서 학습에 사용해야 함.
• Offline RL(Reinforcement Learning) 알고리즘은 추가적인 데이터 수집 없이(=env와의 상호작용 없이), 기존에 수집된 데이터 내에서 Policy를 효율적으로 학습할 수 있게 함.

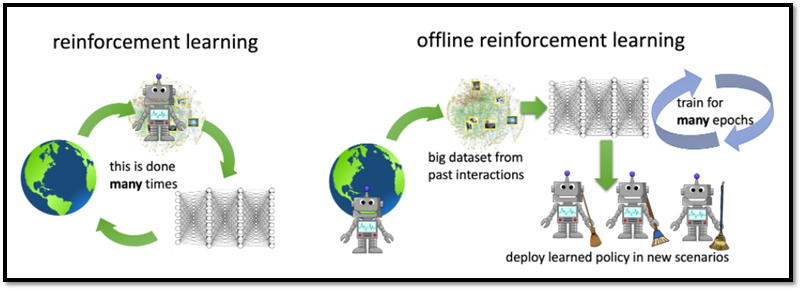
기존 RL과 Offline RL의 차이점 // 출처 : https://bair.berkeley.edu/blog/2020/12/07/offline/

• 하지만 Offline RL에는 한계점이 존재 : Q-value(Action-Value Function)의 과대 현상(Overestimation)발생
  
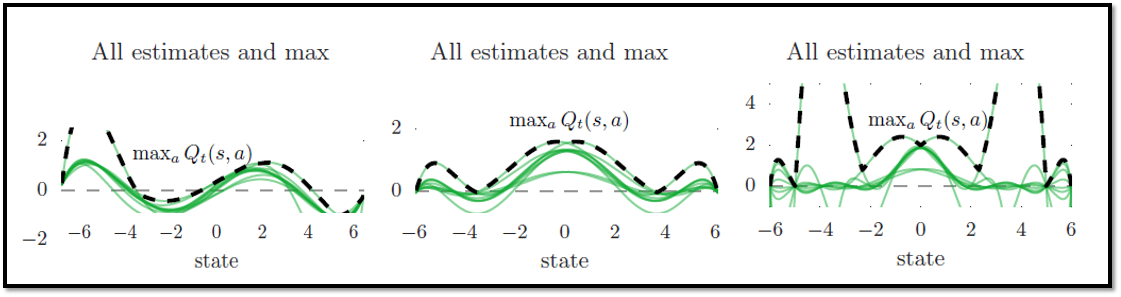
  Q-value의 Overestimation 현상 // 출처 : DDQN paper

• Overestimation의 원인은 여러가지가 있지만, 본문에서는 아래의 원인을 언급함.

• Overestimation의 원인 : Data Distributional Shift (데이터 분포 변화)

• Offline RL의 데이터 종류는 offline 데이터(behavior policy로 수집한 데이터)와 online 데이터(기존 RL 방식으로 학습 진행 시 수집되는 데이터)로 2가지인데, 이 두 데이터의 분포가 상당히 다른 것을 아래의 그림에서 확인할 수 있음
  
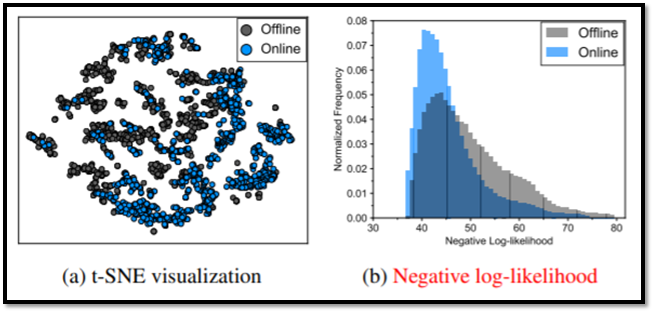
  D4RL 알고리즘에서 walker2d-medium의 데이터로 학습했을 때, online과 offline 데이터의 분포의 시각화 // 출처 : ADDRESSING DISTRIBUTION SHIFT IN OFFLINE-TO-ONLINE REINFORCEMENT LEARNING (paper)

<해결책 : Conservative Q-Learning>

• 본문에서는 Q-value의 Overestimate 현상을 해결하기 위해, CQL : Conservative Q-Learning 알고리즘을 제안함

• CQL는 아래의 그림과 같이, Q-function에 따른 policy의 Q-value(estimate Q-value)가 true Q-value보다 낮아지도록 유도
  
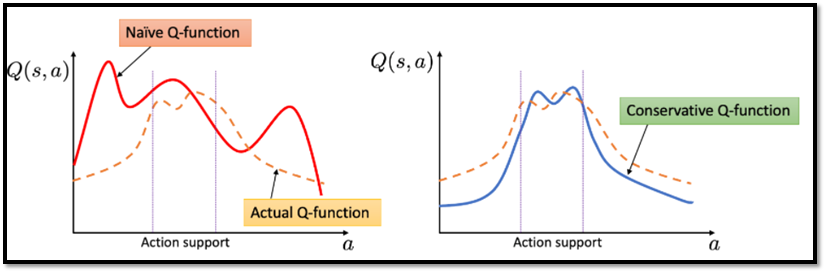
  기존 Q-function과 Conservation Q-function의 비교 // 출처 : https://bair.berkeley.edu/blog/2020/12/07/offline/

• 본문에서 CQL이 이론적으로 현재 policy의 Q-value의 하한을 산출하고, 이론적 수식 개선을 통해 policy 학습 절차에 통합되어최적화에 용이한 것을 보여줌

• 실제로 CQL은 기존의 Deep Q-learning(Discretre Domain)과 Actor-Critic(Continuous Domain) 알고리즘 위에 구현하기 쉬운 간단한 Q-value Regularizer를 사용하여 Standard Bellman error objective를 강화할 수 있음
  

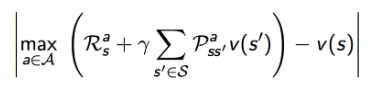
• 본 연구 실험 결과에서 볼 수 있듯이, Discrete하고 Continuous한 Control Domain에서 모두, CQL은 기존 Offline RL보다 2~5배 높은 final return을 달성함

Introduction

<Offline RL 장점 및 한계점>

• 최근 RL은 Deep Neural Network로 Q-function을 근사화함으로써 많은 진보가 있었고, Robotics[31], Strategy Games[4] 그리고 Recommendation System[37] 분야에서 뛰어난 성과가 나오고 있음
  
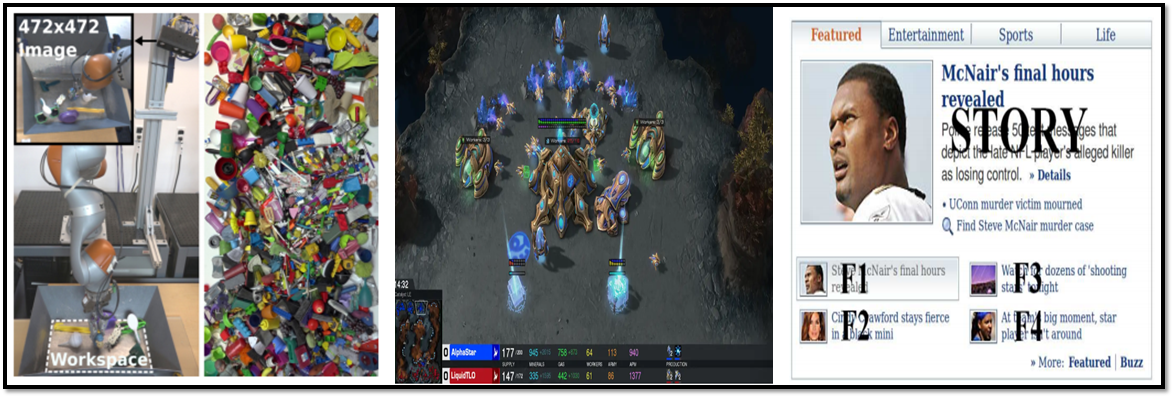
  (좌) : Robotics_Pick & Place, (중) : Game_AlparStar, (우) : Recommendation System_yahoo // 출처 : 본문 참고문헌 31, 4, 37
• 그러나 RL을 실제 세계에 적용하는 것은 Practical Challenge가 존재함
• RL Challenge : RL은 학습 시, environment와 active한 상호작용(interaction)을 통해 얻을 수 있는 Online 데이터가 필요
• 실제 세계 혹은 환경과 상호작용하는 것(=online 데이터를 수집하는 것)은 offline 데이터 수집에 비해, 비용이 많이 들고 위험함 (실제 로봇을 학습하려면 실제 로봇을 구비해야 하고, 학습 도중에 로봇이 고장나면...쉣...)
  이를 보완하기 위해 Offline Reinforcement Learning(또는 Batch RL이라고도 불림) 알고리즘이 등장!!
  
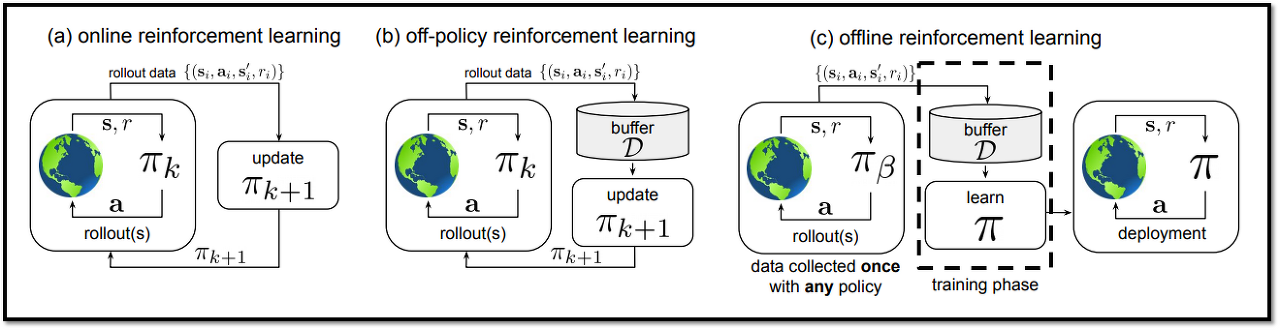
  기존 RL vs Offline RL 차이 도식도 // 출처 : Offline Reinforcement Learning: Tutorial, Review, and Perspectives on Open Problems (paper)
• Offline RL은 env와 상호작용 없이, 이전에 수집된 대량의 데이터셋으로부터 학습 진행
• Offline 데이터 수집의 대표적인 방법 : 시뮬레이션에서 데이터 수집
  
  Offline 데이터 수집 예시 : 자율주행을 위해 GTA 게임에서 데이터 수집 // 출처 : https://techrecipe.co.kr/posts/29186
• 그러나! Offline RL에는 한계점이 있음 : Data를 수집하는 Policy와 학습하는 Policy 사이의 Distributional Shift 발생
• 직관적으로 생각해봤을 때, 시뮬레이션에서의 데이터와 현실 데이터는 시각적으로도, 물리적으로도 차이가 있기 때문에 이러한 Shift가 발생한다고 이해하면 될 것 같습니다!
• Distributional Shift의 이해에 대해 도움이 될만한 링크 -> 4.9.1.1. Covariate Shift와 4.9.2.2. Self-Driving Cars를 참고하면 됩니다! : https://d2l.ai/chapter_multilayer-perceptrons/environment.html

<Offline RL 한계점 원인 및 극복 방안>

• Offline RL의 구현 방법 중 하나인 Offline 셋팅에 Off-Policy RL 알고리즘을 적용하는 것은 Out of Distribution과 Overfitting 문제 때문에 좋지 않은 성능을 보임
• 이러한 문제의 원인 : Q-Value의 Overestimate 현상 때문
• 본 연구에서는 이 현상을 true Q-value보다 낮은 값을 제공할 수 있는 Conservative Q Learning을 통해 극복하고자 함
• 실제로 policy 개선과 평가에서 policy 값만을 사용하기 때문에, true Q-value보다 낮은 값을 산출하는 것이 가능함
• 본문에서는 standard value-based RL 알고리즘(DQN, Actor-Critic)에 간단한 수정을 통해 Conservative Q-functions을 학습하는 방법을 제안함
• 이 방법의 핵심 아이디어는 Dataset에 없는 action들의 distribution에서 계산되는 Q-value 값을 최소화하고, 데이터 distribution에 속한 action에 대해 max term을 추가함으로써 이 lower bound를 잘 찾게 하는 것임 (max term에 대한 내용은 3절에서 설명!)

<본문 : CQL의 기여점>

주요 기여점 : CQL 알고리즘 프레임워크 제안 -> 학습 도중에 Out-of-Distribution Action들의 Q-value를 regularizing함으로써, value function의 낮은 추정치를 산출
이론적 분석 : CQL은 lower-bounded Q-functions으로부터 발생할 수 있는 추가적인 under-estimation을 방지 (이에 대한 이론적 분석 내용은 3절에서 설명!)
실험 결과 : 여러 벤치마크에서 CQL이 기존 기법에 비해 2~5배 높은 score을 보여줌으로써, Q-function estimation error에 대해 본문의 접근 방식의 robustness함을 보여줌 (실험 결과에 대한 내용은 6절에서 설명!)

Perliminaries

<MDP 정의>

• 강화학습의 목표 : MDP(Markov Decision Process)에서 누적된 reward의 기댓값을 가장 극대화하는 policy를 학습하는 것
• MDP 구성 : tuple -> (State, Action, Dynamic, Reward, Discount factor)
• Dynamic Function : Next_State로 갈 확률 분포

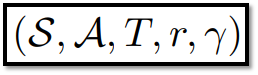MDP의 형태 // 출처 : 원문
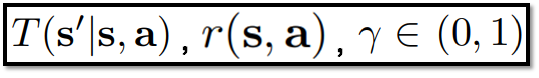Dynamic, Reward, Discount Factor의 정의 // 출처 : 원문

• Behavior Policy, πβ(a|s) : Offline 데이터 수집에 사용되는 policy
• Discounted Margnial State-Distribution of Behavior policy, dπβ(s) : policy π를 따랐을 때의 state 확률 분포
• D : Dataset

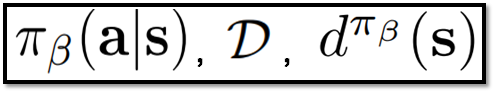
behavior policy, Dataset, discounted marginal state-distribution of behavior policy의 정의 // 출처 : 원문

• 모든 state는 Dataset D에 포함됨
• empirical behavior policy, ^πβ(a|s) : state s에서 action a를 할 확률
• r(s,a)는 정의한 R_max 값보다 크지 않음

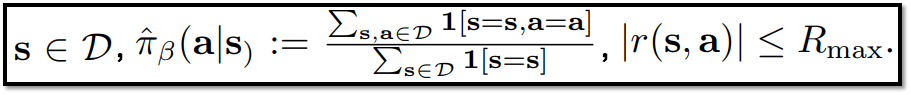state 범위, empirical behavior policy, reward 범위에 대한 정의 // 출처 : 원문

<Off-Policy & Actor-Critic 개요>

• Off-policy RL은 파라미터화된 Q함수와 policy를 포함
• Actor-Critic의 경우, Q함수 : Critic Network, Policy : Actor Network

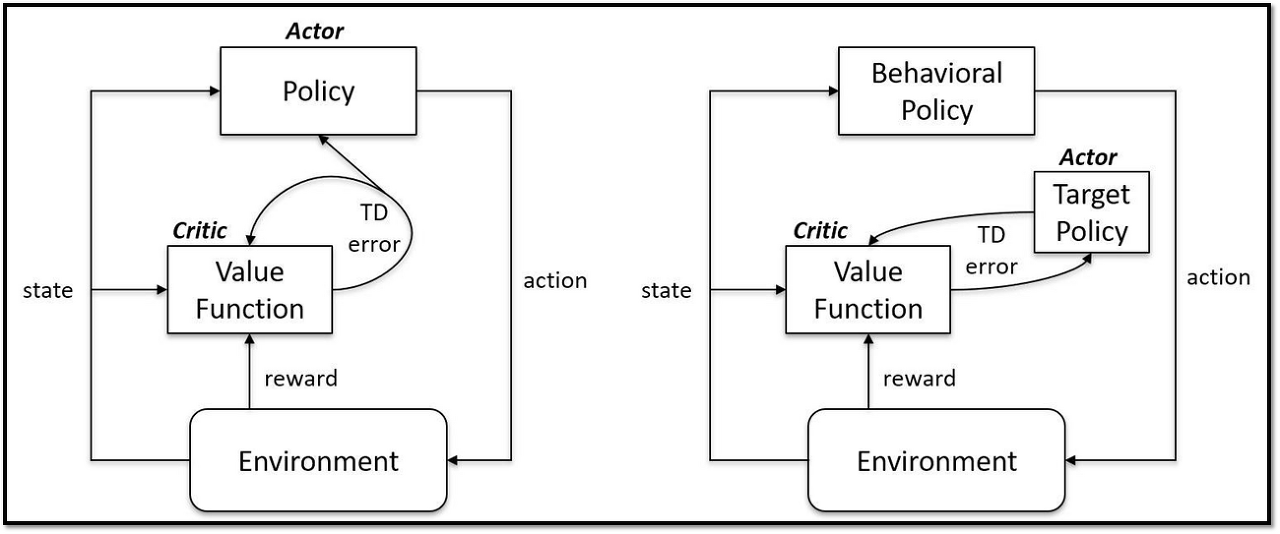
On-policy (좌), Off-policy (우) // 출처 : https://www.reddit.com/r/reinforcementlearning/comments/hd35zt/onpolicy_vs_offpolicy_actorcritic/

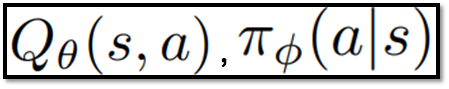
파라미터화된 Q함수와 policy 정의 // 출처 : 원문
Q Learning의 학습 과정 : Bellman optimality operator와 True Q-Value의 차이를 파리미터에 업데이트하는 것을 반복 적용

Bellman Operator 수식 // 출처 : 원문

Q-vlaue의 기댓값이 최대화 되는 action을 향하도록 policy를 improve 및 evaluation

Actor-Critic 내용 정리 -> 위 수식은 Critic Network, 아래 수식은 Actor Network의 업데이트 대한 내용 // 출처 : 원문

<Offline RL 개요>

• Off-policy를 기반으로 한 Offline RL 알고리즘들은 학습 도중 action distribution shift 문제 발생

• action distribution shift 원인 : policy evaluation에서 estimate Q-function, ^Q(s, a)는 learned policy π_k에서 sample된 action을 사용하지만, True Q-function, Q(s,a)은 오로지 dataset D를 수집할 때 사용하는 behavior policy π_b, 즉 데이터셋에서 sample된 action을 사용 -> Dataset에 없는 action에 대해 평가해야 하는 경우 발생
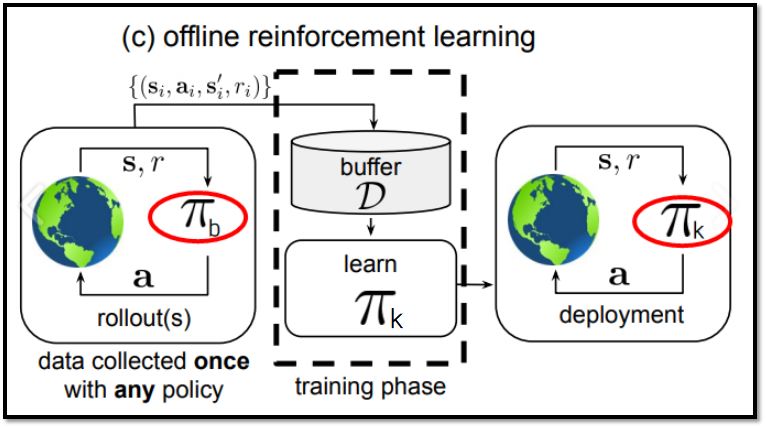  action distribution shift 원인 : 서로 다른 policy의 action을 학습에 사용 // 출처 : Offline Reinforcement Learning: Tutorial, Review, and Perspectives on Open Problems (paper)

• policy는 Q-value를 극대화하는 방향으로 학습되기 때문에, 본적 없는 action들은 높은 Q-value로 out-of-distribution actions으로 편향될 가능성이 큼

• 이 원인은 데이터를 수집하는 behavior policy π_b와 Q-function 값을 예측하는 learned policy π_k가 분리되어 있기 때문에 발생하므로, 하나의 policy로 합쳐서 모든 데이터 수집 및 학습을 실제 환경에서 action을 시도하고 실제 값을 관찰하면 이러한 error를 수정할 수 있음

• 하지만 환경과의 상호작용은 비용이 많이 들고 위험하기 때문에 거의 불가능하므로, Offline RL에서 OOD (out of distribution) action에 대한 Q-value 수정이 어려움 (policy를 합치는건 Offline RL을 사용하는 목적이 사라지는 것이기도 함...)

• 전형적인 offline RL 알고리즘은 learned policy π_k에 제약을 걸어서 이 문제를 완화시킴

• 그러나 근본적인 원인을 기반으로 제시한 해결책이 아니므로, 실제 환경에서 test를 할 때 state distribution shift 문제가 발생할 수 있으며, π_k의 true 값 기준을 측정하는 estimator를 추가 생성해야해서 알고리즘이 복잡해짐

The Conservative Q-Learning (CQL) Framework

1. Conservative Off-Policy Evaluation

<목표에 대한 개요>

목표 : Value Function인 Vπ(s)의 값(state s에 대한 기댓값)을 예측하는 것
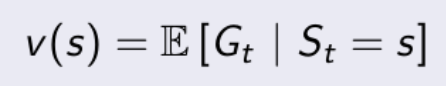Value Function 정의 // 출처 : https://dnddnjs.gitbooks.io/rl/content/value_function.html
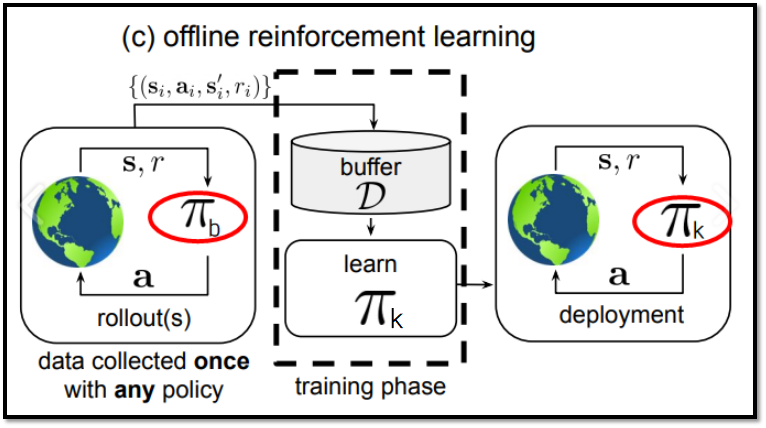Offline RL 개념도 // 출처 : Offline Reinforcement Learning: Tutorial, Review, and Perspectives on Open Problems (paper)

• Vπ(s) : behavior policy π_β(a|s)에 의해 생성되는 데이터셋 D에 의해 학습되는 Learned policy π_k의 Value Function
• 본 연구의 관심사 : overestimation 현상을 방지
• 해결책 : standard Bellman error objective에서 out-of-distribution action들의 Q-values를 최소화함으로써 conservative, lower-bound Q-function을 학습 -> OOD action의 Q-value에 대한 규제화 필요 (regularization 혹은 penalty)

<아이디어 구체화 1 : Objectives for Q-function training -> lower bounds Q-value>

• 핵심 아이디어 : state-action 쌍인 µ(s,a)의 특정 distribution, 그 중에서 Dataset D에 없는 action도 포함하는 Q-function을 계산하는데, 이에 대한 Q-function 값을 최소화시킴 (수식 1의 빨간 박스 영역)
• μ(a|s) : 데이터셋에 있는 state를 input으로 받고 action을 output으로 내는데, 이 때의 action은 데이터셋이 속하지 않은 action일 수도 있음
• 수식 1의 빨간 박스 영역은 trade off 계수 α로 값의 영향력을 조절할 수 있으며(아래 수식 1의 빨간 박스), α가 충분히 크면 모든 state, action에 대해 ^Qπ(s, a) <= Qπ(s,a)를 만족
• 이에 대한 증명은 Theorem 3.1에서 볼 수 있음
  수식 (1) : Basic CQL evaluation // 출처 : 원문
  수식 (1)의 부가 설명 // 출처 : CQL (long presentation) - Google Slides
  수식 (1)의 증명 // 출처 : 원문

<아이디어 구체화 2 : Value Function에 집중>

• Action-value Function, Q(s, a) 대신 Value Function, Vπ(s)의 estimate하는 것에 집중한다면, lower-bounds : ^Qπ <= Qπ 를 더 좋게 개선할 수 있음
• 수식 (2)의 빨간 부분 같이, Q-value maximization term을 추가
• Q-value maximization term의 특징은 data distribution인 ^πβ(a|s)의 범위에서 존재
• 파란색 영역을 최소화하는 Q 값을 찾아야 하는데, 파란색 영역 중 왼쪽 기댓값은 Dataset에 없는 action에 대해서도 Q-function을 계산하기 때문에 overestimate 경향 존재 -> 이에 따라 오른쪽 기댓값(Offline 데이터 수집에 사용하는 behavior policy에 속하는 action을 사용)도 값이 커져야 파란색 영역을 최소화할 수 있으므로, 오른쪽 기댓값(빨간 글씨)을 maximize하게 됨
• 이로써 µ(s,a) = π(a|s)일 때, ^Vπ(s) <= Vπ(s)를 보장할 수 있음 (^Qπ <= Qπ는 보장하지 못하지만!)
• • 이때의 policy는 learned policy 같지만... 논문에 정확한 언급이 없네요 ㅜㅜ
• 이에 대한 증명은 Theorem 3.2에서 확인 가능
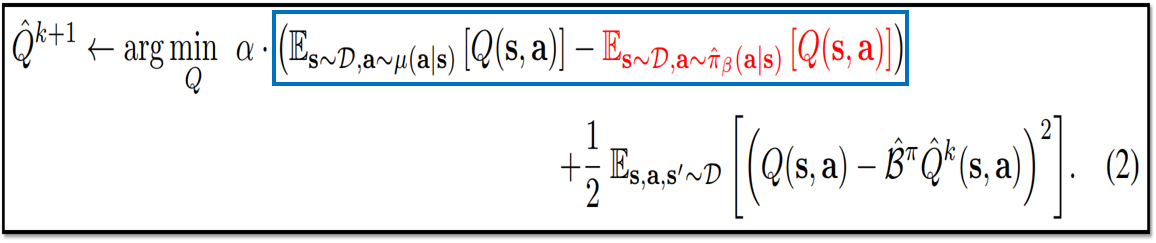  수식 (2) : CQL evaluation의 변형 수식 // 출처 : 원문
  수식 (2)의 부가 설명 // 출처 : CQL (long presentation) - Google Slides
  수식 (2)의 증명 // 출처 : 원문

In summary

• 수식 (1) - basic CQL evaluation : Qπ(a,s)(true Q-function)보다 작은 값을 지니는 ^Qπ(a,s)(estimate Q-function) 학습
• 수식 (2) - variations CQL evaluation : Vπ(s)(true Value-functnon)보다 작은 값을 지니는 ^Vπ(estimate Value-function) 학습
• trade off 계수 α : 적합한 α의 경우, 위 수식 1,2의 lower bounds를 항상 보장

2. Conservative Q-Learning for Offline RL

<아이디어 구체화 3 : Conservative Q-function for Policy Improvement>

• 기존 수식 1, 2(Off-Policy)를 Offline RL에 적용하는데 발생하는 한계점 : policy의 최적화를 위해 policy evaluation(target policy or Critic Network)와 policy improvement(behavior policy or Actor Network)를 번갈아가며 연산하기 때문에, Policy Optimization의 연산량이 너무 큼

• Optimization 해결책 : policy evaluation과 improvement를 한번에 진행하기 -> policy ^π_k는 Q-function에서 유도되기 때문에, policy improvement는 현재 Q-function 값을 최대화하는 policy를 근사화할 수 있는 µ(s,a)를 선택하면 됨 (max µ)

• 수식 (3)에서 R(µ)이라는 regularizer를 추가함으로써 CQL(R)이라고 명명함

• R(µ)의 종류에 따라 CQL 특성이 변화하며, 이에 대한 내용은 (CQL Variants)에서 설명 예정

• CQL은 Q-learning 알고리즘 뿐만 아니라 Actor-Critic 알고리즘에도 적용 가능

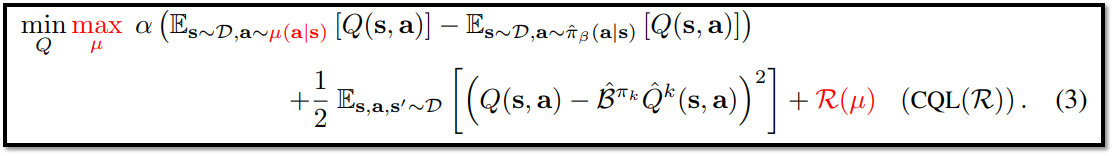  수식 (3) : CQL evaluation의 변형 수식 // 출처 : 원문 수식 (3)의 부가 설명 // 출처 : CQL (long presentation) - Google Slides
  수식 (3)의 부가 설명 // 출처 : CQL (long presentation) - Google Slides

• Theorem 3.3을 통해 CQL은 모든 state에 대해 ^V(s) <= V(s) 임을 증명

• learned policy(^πk+1)와 optimal policy(π^Qk)가 같으면, Theorem 3.3의 LHS(Dtv(^π_k+1, π^Qk))은 CQL update의 k+1번째의 ^V_k+1의 값에서 발생한 conservatism 값과 같음

• D_tv : Total Variation Divergence

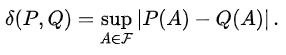  Total Variation Divergence 수식 // 링크 : https://en.wikipedia.org/wiki/Total_variation_distance_of_probability_measures

• 그러나 learned policy와 optimial policy는 다를 수도 있기 때문에, RHS(ε)는 두 policy의 차이로 인해 발생하는 overestimate의 최댓값으로 볼 수 있음

• lower bound를 얻기 위해서, underestimation 값이 커야 하는데, 이는 ε를 작을 경우, 즉 policy가 천천히 변경되어야 함

Theorem 3.3 CQL의 Lower bounds 성능 증명 // 출처 : 원문

• 마지막으로 CQL의 Q-function이 "gap-expanding" 하게 업데이트 됨을 보여줌
• Gap-Expanding : PDataset에 있는 action(In distribution action)의 Q-value와 Dataset에 없는 action(Out of distribution action)의 Q-value의 차이가 Predict Q-function이 True Q-function 보다 해당하는 차이보다 큰 경우를 의미
• 이것은 policy π_k(a|s)가 dataset distribution πˆβ(a|s)에 더 가까워지도록 하는 것을 의미함
• 따라서 CQL update는 Offline RL에서 주요 관심사였던 OOD action과 distribution Shift 문제를 방지할 수 있음
• 만약에 sampling 오류로 인해 OOD action가 발생하고, 이에 따라 학습된 Q-value보다 높아지면, in-distribution actions을 선호하는 Q-value를 사용하여 policy가 업데이트된다는 점에서, CQL backups은 보다 robust해질 것이라고 예상됨
  Theorem 3.4 Gap-Expanding 정의 // 출처 : 원문

(CQL Variants)

• 유형 (1) : CQL(H)

• R(µ)를 H(µ)로 설정하고 풀이한 결과가 수식 (4).
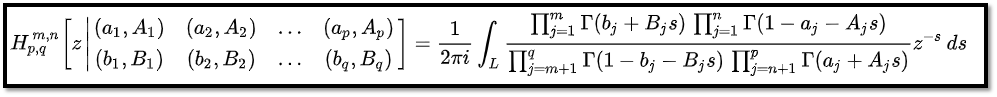  H(x) 함수 정의! 그만 알아보도록 하자.. // 출처 : https://en.wikipedia.org/wiki/Fox_H-function
  수식 (4) 정의 -> H(µ) regularizer을 사용했을 때의 CQL 수식 // 출처 : 원문

• 유형 (2) : CQL(ρ)

• R(µ) 대신 KL-divergence regularizer로 설정하고 풀이한 결과가 수식 (7)

• CQL(ρ)는 고차원 action space에서 더 안정적으로 수렴하며, 이에 대한 분석은 6.Experimental Evaluation의 Table 2에서 진행할 예정.

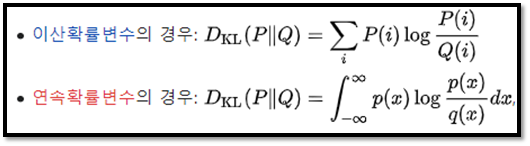KL-divergence 정의! 그만 알아보도록 하자.. // 출처 : https://ko.wikipedia.org/wiki/%EC%BF%A8%EB%B0%B1-%EB%9D%BC%EC%9D%B4%EB%B8%94%EB%9F%AC_%EB%B0%9C%EC%82%B0

In summary

• (1) CQL RL 알고리즘은 충분한 α값과 함께 Q-value의 lower-bound를 학습할 수 있음
• 이는 final policy가 최소 estimated value를 얻을 수 있음을 의미함
• (2) CQL Q-function이 Gap-Expanding임을 보여줌
• 이는 in-distribution action과 out-of-distribution actions 간의 gap을 over-estimate하여 OOD action을 방지해야 함

3.Safe Policy Improvement Guarantess

(Provide a safe policy improvement result for CQL)

• empirical return of any policy π, J(π, ^M) : Dataset D에 의 해 관찰된 transitions(s, a, r, s')에 의해 생성된 emprical MDP, ^M에 대한 policy π의 discounted return을 의미
• J(π, M) : actual underlying MDP, M에 대한 policy π의 discounted return을 의미

Theorem 3.5 CQL의 최적화 과정 // 출처 : 원문

• Theorem 3.5은 CQL이 RL empirical objective의 최적화 과정을 보여줌 (파라미터 업데이트)
• 또한 D_cql에 의존하는 penalty를 통해 learned policy π이 behavior policy ^πβ와 크게 차이 나지 않는 것을 보장함
  Theorem 3.5의 증명 일부 // 출처 : 원문

• Learned Policy와 Behavior Policy가 다르면 D_CQL 값은 양수가 됨 -> 이 값이 J(π, ^M) 즉 기댓값에서 빠지게 되므로, 두 policy가 같아지도록 학습하게 됨

위 내용에 대한 설명 // 출처 : BAIR LAB의 CQL 논문 리뷰 PPT

(In summary)

• (1) CQL은 penalized empirical RL objective를 최적화하며, high-confidence safe policy improvement를 보장함

Practical Algorithm and Implementation Details

• CQL 알고리즘은 두 유형을 기반으로 만듦 : Q-learning & Actor-Critic -> Discrete & Continuous Domain을 모두 고려함
• Q-Learning은 DQN(Deep Q Network)을 참고했고, Actor-Critic은 SAC(Soft Actor Critic)를 참고함
• 모델 학습하는데 CQL(H)를 사용
• CQL은 이전 Offline RL 알고리즘에서 사용했던 policy constraint를 사용하지 않음
• 따라서 추가적인 behavior estimator를 설정할 필요가 없어서, 본 알고리즘은 간단해짐
• α 값은 Discrete control에서는 고정했고, Continuous Control에서는 Lagrangian Dual Gradient Descent를 통해 자동으로 조절함
  CQL 수도 코드 // 출처 : 원문

Experimental Evaluation

<실험 개요>

• CQL 모델 1 : actor-critic CQL, using CQL(H)
• CQL 모델 1의 데이터셋 : continuous control datasets from the D4RL benchmark
• CQL 모델 1과 비교한 이전 offline RL 모델들 : BEAR, BRAC, SAC, BC
  D4RL 데이터셋 종류 // 출처 : https://sites.google.com/view/d4rl/home

(Gym domains : Continuous Control by actor-critic CQL)
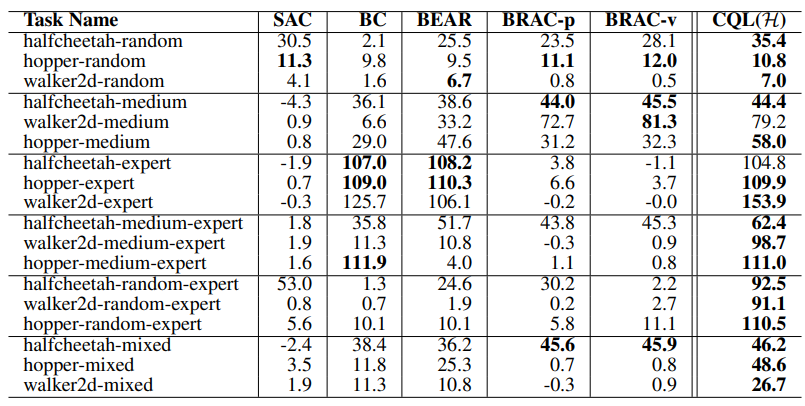Tabel 1. D4RL의 gym domain에서 CQL(H)와 prior methods의 성능 비교 // 출처 : 원문

GYM Domain 사진 예시 // 출처 : GYM 홈페이지

• CQL(H)는 BEAR, BRAC, SAC 그리고 BC와 같은 prior methods와 유사하거나 더 좋은 성능(game score)을 냈으며, 특히 난이도가 mix된 (mixed, meduim-expert, random-expert) 도메인에서 prior method보다 2~3배 더 높은 성능을 달성하면서 robust함을 증명

(AntMaze, Adroit, Kitchen : Continuous Control by actor-critic CQL)
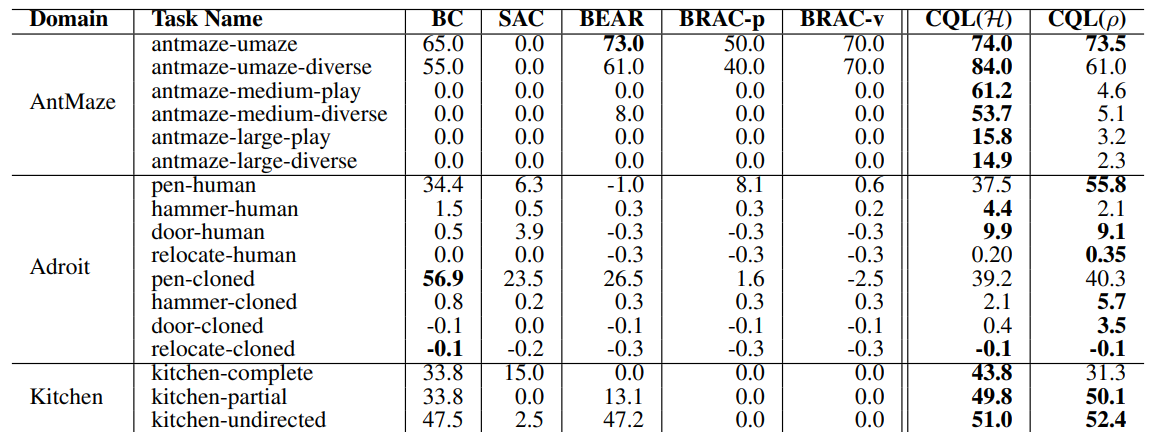Tabel 2. D4RL의 Antmaze, Adroit, Kitchen의 성능 비교 // 출처 : 원문
AntMaze, Adroit, FrankaKitchen 예시 // 출처 : https://sites.google.com/view/d4rl/home

• Antmaze : medium, large task에서 prior methods는 모두 점수가 0인데, CQL만 유일하게 0이 아닌 점수를 얻음
• Adroit tasks : 24 자유도의 로봇 손 제어로 인해 action space 차원이 매우 높으나, CQL이 prior methods 중에서 가장 성능이 좋음 & CQL(H)보다 CQL(ρ = ^π_k−1)이 더 높은 성능을 보이는데, 고차원의 action space에 대한 해석이 뛰어난 것으로 보임
• Kitchen : 9자유도의 로봇 머니퓰레이터 제어를 해야 하며, 역시 CQL 성능이 가장 뛰어남

Figure 1. Atari Domain에서 CQL, REM, OR-DQN의 성능 비교 // 출처 : 원문
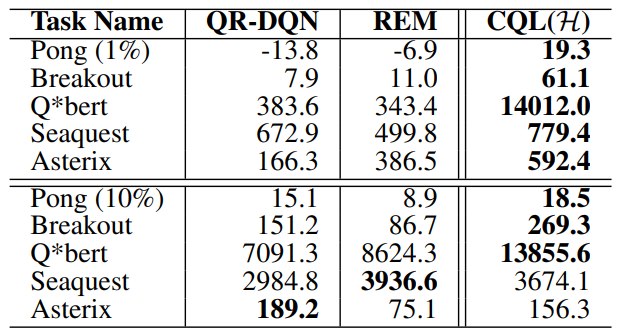Tabel 3. CQL, REM, QR-DQN의 성능 비교표 // 출처 : 원문

• Discrete Domain에서 역시, CQL이 prior methods와 성능이 비슷하거나 더 높은 것을 확인할 수 있음
  Tabel 4. True Policy Value와 Predict Policy Value와의 차이에 대한 표

• CQL의 Predict Policy Value는 True Policy Value보다 작음을 보여줌으로써, Theorem 3.2를 실험 결과로써 증명함

• CQL(H)는 CQL(Eq 1)보다 덜 적게 conservative함

Discussion

• 본 연구에서는 Conservative Q-Learning(CQL) : policy value보다 lower bound를 배우는 offline RL을 위한 알고리즘 프레임워크를 제안함
• 본 실험 결과에서 CQL이 복잡한 제어와 raw image observation을 포함한 광범위한 offline RL task에서 기존 방법들을 능가하는 것을 보여줌
• CQL의 단순성과 효율성은 광범위한 실세계 offline RL 문제에 대해 좋은 선택임
• 그러나 아직 여러가지 문제가 남아 있음
• 문제 (1) : 선형 및 비선형 함수 근사 사례의 부분 집합에서 Q 함수에 대한 하한을 학습한다는 것을 증명하지만, Deep Neural Networks를 갖춘 CQL에 대한 이론 분석은 향후 연구를 위해 남겨져 있음
• 문제 (2) : Offline RL 방법은 지도 학습과 같은 방식이기 때문에 over fitting 문제가 발생할 수 있으므로, 지도 학습에서 사용되는 early stopping 방법과 같이 효과적인 조기 중지 방법을 고안해야 함