
알고리즘 성능 평가
알고리즘의 성능 평가는 어떻게 할 수 있을까?
알고리즘 성능을 평가하기 위해 '복잡도(Complexity)'의 척도를 사용한다.
그중 시간 복잡도와 공간 복잡도의 개념이 나오며, 동일한 기능을 수행하는 알고리즘이 있을 때 복잡도가 낮을 수록 좋은 알고리즘이라 말한다.
복잡도 (Complexity)
- 알고리즘의 성능, 효율성을 나타내는 척도
- 시간 복잡도(Time Complexity)와 공간 복잡도(Space Complexity)로 나눌 수 있다.
- 각 알고리즘이 주어진 특정 크기의 입력(n)을 기준으로 수행시간(연산) 혹은 사용공간이 얼마나 되는지 객관적으로 비교할 수 있는 기준을 제시한다.
다시 말해, 복잡도는 어떤 알고리즘이 효율적인지를 판단하는 척도!
시간 복잡도 (Time Complexity)
시간 복잡도는 특정 알고리즘이 어떤 문제를 해결하는데 걸리는 시간을 의미 한다.
시간 복잡도이지만 실행 시간이 아닌 연산 횟수를 세는 이유
- 모든 OS, IDE, 플랫폼에서 동일한 결과가 나오지 않는다.
- 실행 시간 측정을 위한 또다른 방법이 필요하다.
빅-오 표기법
빅오 표기법(Big-O notation)은 복잡도를 나타내는 점근 표기법 중 가장 많이 사용되는 표기법이다.
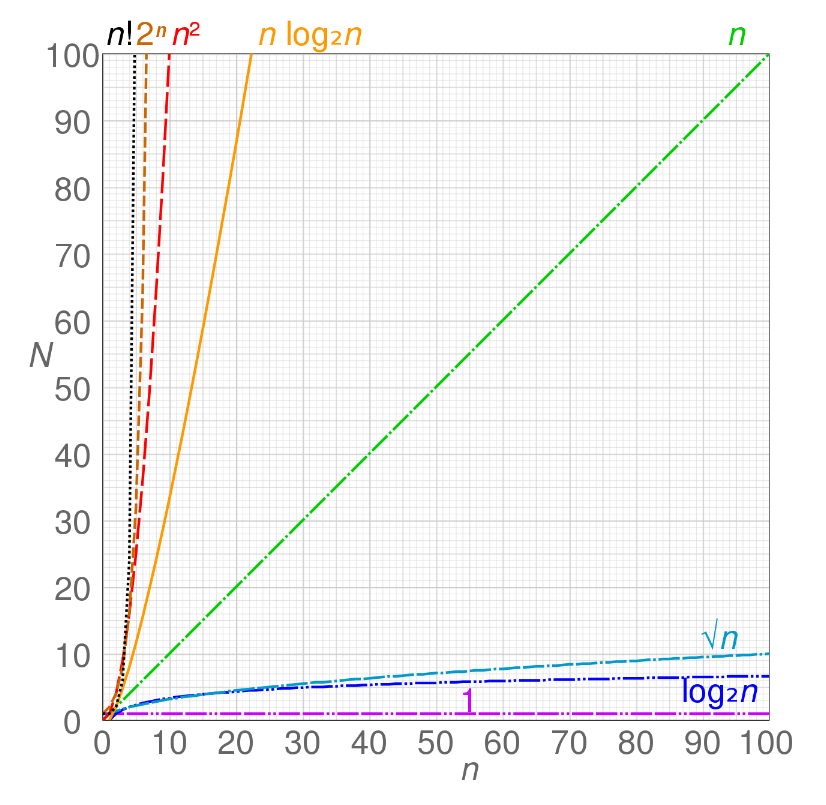
알고리즘 효율성을 상한선 기준으로 표기하기 때문에 최악의 경우를 계산하는 방식이다. (알고리즘 효율성은 값이 클수록, 즉 그래프가 위로 향할수록 비효율적임을 의미)
O(1) (Constant)
입력 데이터의 크기에 상관없이 언제나 일정한 시간이 걸리는 알고리즘.(push, pop)
function f(arr,i) {
return arr[i]
}
let result = f([1,2,3,4,5], 1)
console.log(result) // 2O(log n) (Logarithmic)
입력 데이터의 크기가 커질수록 처리 시간이 로그(log: 지수 함수의 역함수) 만큼 짧아지는 알고리즘.
예를 들어 데이터가 10배가 되면, 처리 시간은 2배. (이진 트리 탐색)
function binarySearch(arr, target) {
let left = 0;
let right = arr.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
if (arr[mid] === target) {
return mid; // 찾은 경우 인덱스 반환
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // 찾지 못한 경우 -1 반환
}O(n) (Linear)
입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘.
예를 들어 데이터가 10배가 되면, 처리 시간도 10배(for문)
function f(n){
let count = 0;
for (let i = 0; i < 5*n; i++){
count+=1;
}
return count;
}입력된 n번에 대하여 count에 n * 5번만큼 더하는 연산을 수행하고 있으므로 f(n) = 5n 이다. 하지만 빅오표기법에서는 모든 상수는 무시한다.
O(n log₂ n) (Linear-Logarithmic)
데이터가 많아질수록 처리시간이 로그(log) 배만큼 더 늘어나는 알고리즘.
예를 들어 데이터가 10배가 되면, 처리 시간은 약 20배(퀵 정렬(quick sort), 병합정렬(merge sort), 힙 정렬(heap Sort))
function mergeSort(arr) {
if (arr.length <= 1) {
return arr; // 배열이 하나 이하의 요소만을 포함하면 정렬이 끝난 것으로 간주
}
const middle = Math.floor(arr.length / 2);
const left = arr.slice(0, middle);
const right = arr.slice(middle);
// 재귀적으로 왼쪽과 오른쪽 배열을 정렬하고 병합
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
let result = [];
let leftIndex = 0;
let rightIndex = 0;
// 두 배열을 병합하여 정렬된 결과 생성
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex++;
} else {
result.push(right[rightIndex]);
rightIndex++;
}
}
// 남은 요소들을 결과에 추가
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
O(n²) (quadratic)
데이터가 많아질수록 처리시간이 급수적으로 늘어나는 알고리즘.
예를 들어 데이터가 10배가 되면, 처리 시간은 최대 100배(이중 for 문, 삽입정렬(insertion sort), 버블정렬(bubble sort), 선택정렬(selection sort))
function f(n){
for (let i = 0; i < n; i++){
for(let j = 0; j< n; j++ ){
// do something for 1second
}
}
}O(2ⁿ) (Exponential)
데이터량이 많아질수록 처리시간이 기하급수적으로 늘어나는 알고리즘. (피보나치 수열)
function f(n){
if(n < 1){
return 1
}
return f(n - 1) + f(n - 2)
}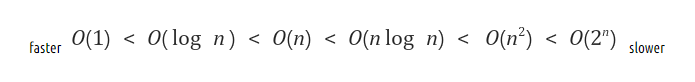
공간 복잡도 (Space Complexity)
공간 복잡도(Space Complexity)란 작성한 프로그램이 얼마나 많은 공간(메모리)을 차지하느냐를 분석하는 방법.
하지만 예전에 비해 컴퓨터 성능의 발달로 인해 메모리 공간이 넘쳐나다 보니 중요도는 많이 떨어짐.
알고리즘을 실행시키기 위해 필요한 공간(space)는 두 가지로 나눌 수 있다.
- 알고리즘과 무관한 공간(고정 공간)
코드가 저장되는 공간, 알고리즘 실행을 위해 시스템이 필요로 하는 공간 등 - 알고리즘과 밀접한 공간(가변 공간)
문제를 해결하기 위해 알고리즘이 필요로 하는 공간. 변수를 저장하는 공간, 순환 프로그램일 경우 순환 스택(recursion stack) 등
시간 복잡도 vs 공간 복잡도
시간 복잡도는 얼마나 빠르게 실행되는지, 공간 복잡도는 얼마나 많은 자원(메모리 공간)이 필요한지를 판단한다.
시간 복잡도와 공간 복잡도는 반비례하는 경향이 있어, 보통 알고리즘의 성능을 판단할 때는 시간 복잡도를 위주로 판단한다.