다리 놓기 1010번 python

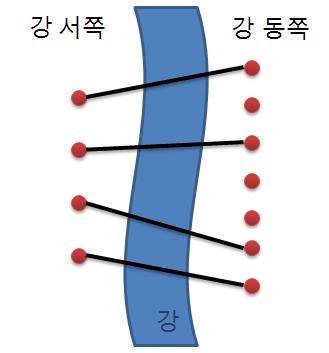
문제 설명

강 서쪽에서 동쪽으로 이어진 다리가 서로 겹쳐지지않게 놓을 수 있는 경우의 수를 구하여라

제한 사항

• 입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
• 각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.

문제 풀이

문제 분석을 위해 주어진 예시를 보며 다리를 놓을 수 있는 경우의 수를 하나씩 세보았다. 강의 서쪽에서 동쪽으로 하나씩 선택하면 경우의 수가 바뀌게 되고 주어진 입축력 예시에서 서쪽 13개 동쪽 29개에서 경우의 수가 엄청나게 많은 걸 봤을때 완전탐색으로 하나씩 세면서 경우의 수를 구하게 되면 불리하다는 생각이 들었다. 수학적 귀납법에 착안해 서쪽과 동쪽에 지점을 하나에서 하나씩 늘려가면서 생각해보니 dp(동적계획법)을 활용하는 문제라는 점을 알았다.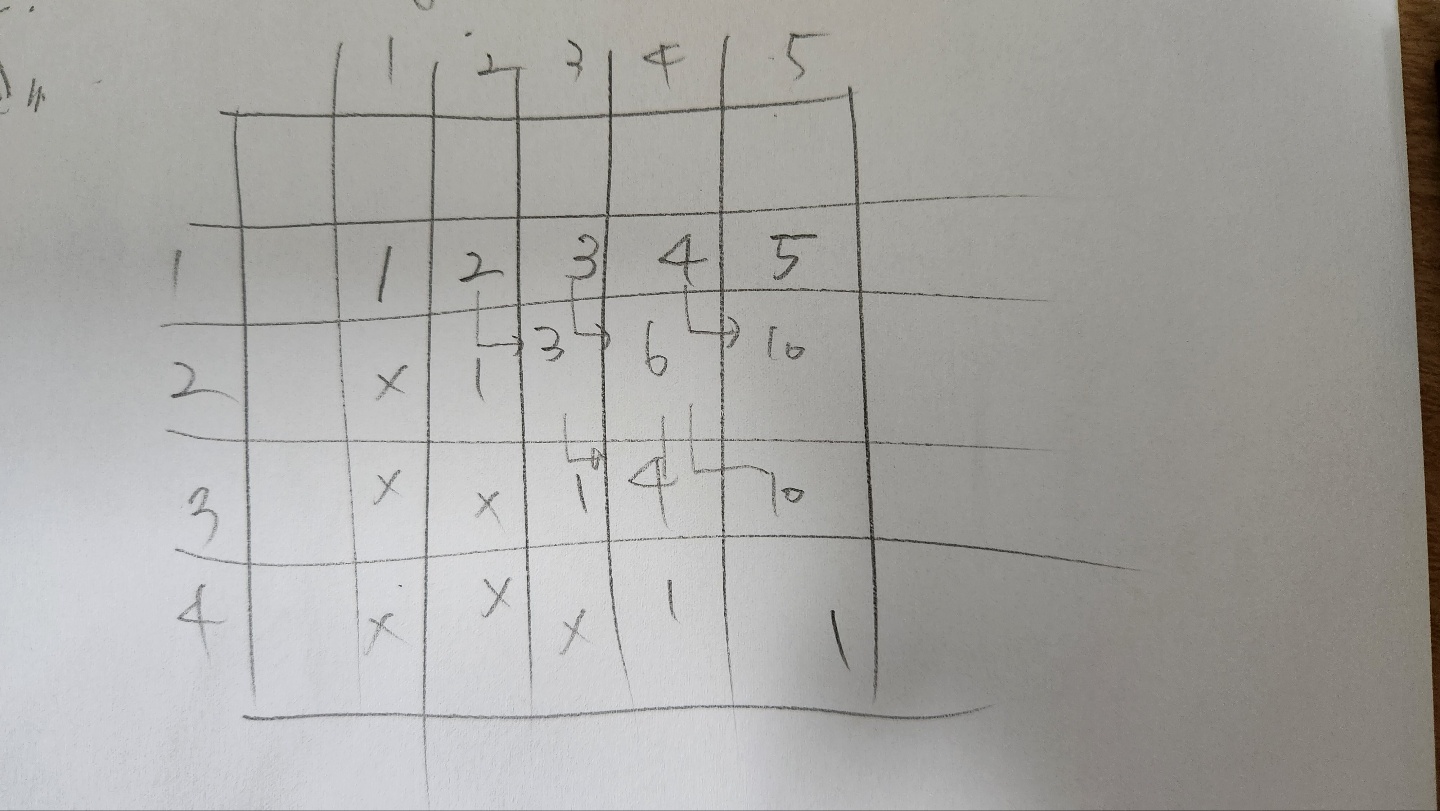
위의 그림은 dp 테이블을 나름 정리한 것이다.
행과 열의 인덱스는 동쪽과 서쪽의 point의 갯수를 의미하고 i -> i의 경우의 수는 1개 고정 1행의 i열은 i개 고정이란 점을 바탕으로 dp테이블을 초기화 하였고, 서쪽과 동쪽의 point를 한 개씩 늘려가며 이전 상태가 다음 상태의 부분집합으로써 가지는 규칙으로 점화식을 세웠다.
코드는 다음과 같다.

tc = int(input())
for _ in range(tc):
    n, m = map(int, input().split())
    dp = [[0] * (m + 1) for i in range(m + 1)]
    for i in range(1, m + 1):
        dp[i][i] = 1
        dp[1][i] = i

    for i in range(2, m + 1):
        for j in range(i + 1, m + 1):
            dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1]
    print(dp[n][m]) # n개의 서쪽에서 m개의 동쪽으로의 경우의 수