컴퓨터 언어 체제(1)

1. 언어

• Context : 프로그래밍 언어를 공부하다보면 "Context(문맥)" 라는 단어를 종종 마주치게 된다.
  왜냐하면, 프로그래밍 언어도 우리가 일상적으로 사용하는 언어와 마찬가지로 문맥이 결과에 영향을 끼치기 때문이다.
  예를 들어 "눈" 이라는 단어에는 두가지 의미가 있다. 신체 중 얼굴의 일부분을 뜻하는 "눈" 과 기상현상에 의해 하늘에서 내리는 무언가를 의미하는 "눈". 만약 문맥을 파악하지 못한다면, 어떠한 문장에서 "눈" 이 의미하는 것이 무엇인지 알기 힘들어진다. 이를통해 문맥이 내장한 의미를 식별하는 데에 얼마나 중요한지를 알 수 있다.

• 문자 : "집" 이라는 단어를 분해하면 'ㅈ', 'ㅣ', 'ㅂ' 으로 나눌 수 있다. 세개의 기호를 조합하여 하자의 문자를 만드는 것이다. 하지만 이를 조합하는 데에는 순서 또한 중요하다. 집이 빚으로 조합될 수도 있다! 때문에 문자는 그 조합과 순서 또한 중요하다. 지금 쓰는 한글의 구성요소가 (기호, 상자에 들어갈 기호, 상자의 순서) 이렇게 볼 수 있다면, 프로그래밍 언어 또한 똑같은 구성요소를 갖는다고 볼 수 있다.

2. 컴퓨터의 문자 "bit"

Binary(2진법) + Digit(숫자) = Bit

• 비트는 2진법을 사용한다. 비트 문자 상자에는 모스부호처럼 점(.)과 선(-) 처럼 두가지 기호 중에 하나만 담을 수 있다. 여기서 또한 조합과 순서가 중요하다. A는 '-.'이지만 '.-'은 N이 된다. 문맥도 중요한 것이, 기호는 추상적이기 때문에 그 문자 상자에 들어갈 수 있는 기호가 0/1 일 수도 있고, 쌀/보리 일 수도 있다. 문맥이 없다면 언어가 제대로 작동할 수 없다. 누구는 001 이라고 하지만 누구는 쌀쌀보리 라고 할 수도 있기 떄문이다.

3. 논리연산

public class Main {
    public static void main(String[] args) {
        boolean judge = true;
        int num1 = 1;
        int num2 = 1;

        if (num1 + num2 == 2){
            judge = true;
            int sum = num1 + num2;
            logic(sum);
        } else {
            judge = false;
        }
    }
    public static int logic(int sum){
        int answer = 0;
        answer = sum / 2;
        
        return answer;
    }
}

• 프로그래밍 언어를 공부한다면 참과 거짓에 익숙하다. "예" 또는 "아니오" 로 대답할 수 있는 문장을 좀 더 확장시켜서 보자.
• 위의 코드에는 if문을 사용하여, "만약 num1 + num2가 2가 참이면 (확장)두 값의 합에 logic 메서드를 실행하라" 라고 표현하는 것이다. 여기서 다른 비트들이 표현했던 내용으로 다른 비트를 만들어 내는 동작(logic)을 논리연산(logic operation) 이라고 한다.

4. George Boole이 만들어낸 Boolean algebra(불리언 대수)

결합법칙, 교환법칙, 분배법칙이 적용가능한 비트에 대해 사용할 수 있는 연산 규칙 집합

• 기본 불리언 연산자: NOT, AND, OR
  합성연산자: XOR

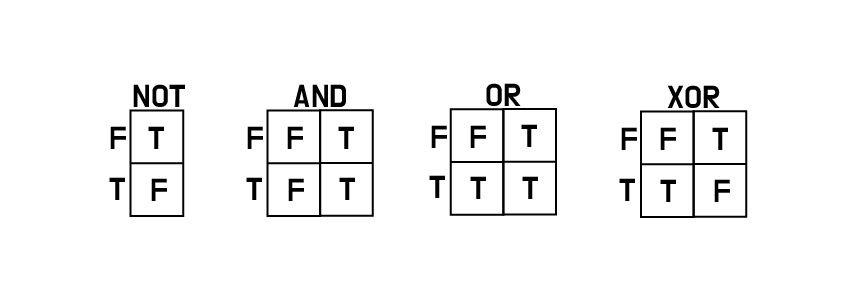
1. NOT: 논리적 반대를 의미한다. 거짓에 NOT을 더하면 참이 되고 참에 NOT을 더하면 거짓이 된다.
2. AND: 둘 이상의 비트에 작용하며 2비트 연산인 경우 모든 비트가 참인 경우만 참이 된다.
3. OR: 둘 이상의 비트에 작용하며 첫번째 비트와 두번째 비트가 다른 값인 경우, 첫번째와 두번째가 둘다 참인 경우에 참이 된다. 더 많은 비트에 연산을 하는 경우 한 비트라도 참이면 결과도 참이다.
4. XOR(exclusive or): OR는 둘 다 참인 경우에도 참이 되었지만 XOR은 둘 다 참이면 거짓이 된다.
5. 불리언 진리표

5. De Morgan's law 드모르간 법칙

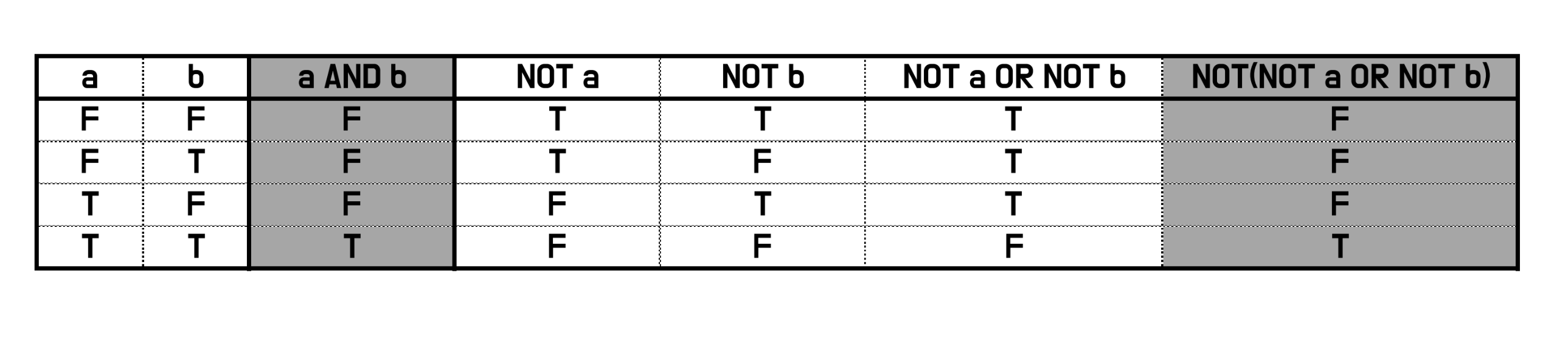
불리언 대수에 적용할 수 있는 법칙: a AND b == NOT(NOT a OR NOT b)

• 드모르간의 법칙 진리표
• 드모르간의 법칙의 진리표를 보면 "NOT 을 충분히 사용하면 AND 연산을 OR 연산으로 대신할 수 있다" 는 것을 알 수 있다. 반대로 OR을 AND로 대신할 수도 있다.
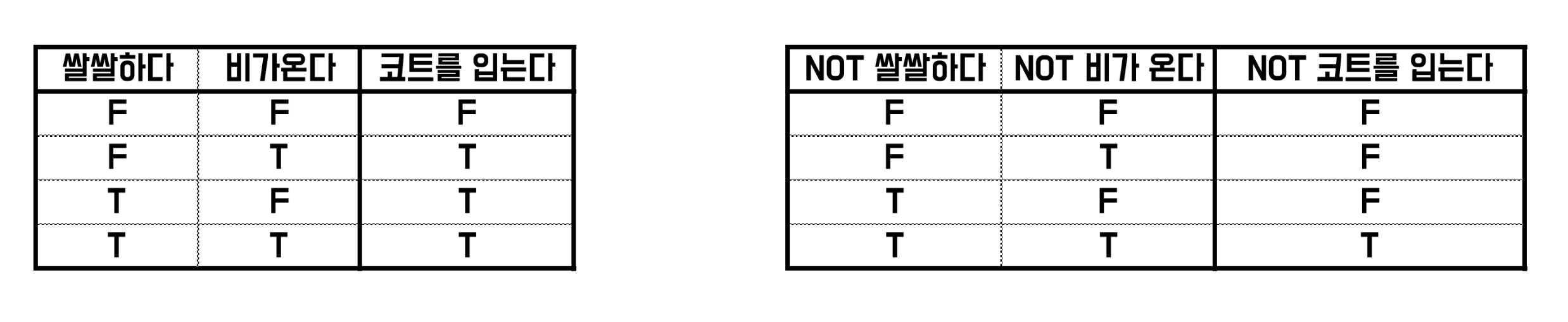
• 입력이 '쌀쌀하다' 와 '비가 온다' 라는 형식일 수 있지만, 'NOT 쌀쌀하다' 와 'NOT 비가 온다' 라는 형식이 될 수도 있다. 위의 예시에서 긍정적인 논리를 정논리 , 부정적인 논리를 부논리 라고 짧게 부르기도 한다.
• 
• 드모르간의 법칙은 부정적인 논리를 구현할 떄에 'NOT NOT 춥다 OR NOT NOT 쌀쌀하다' 로 OR를 사용해야 했을테지만, 연산을 최소로 사용하면 비용을 절약할 수 있다. NOT 연산은 실제 수행에 하드웨어에 비용이 들기 떄문이다. 연산은 연쇄적으로 사용하면 계산이 느려지는데 드모르간의 법칙은 연산비용을 최소화한다는 장점이 있다.

참고서적
"한권으로 읽는 컴퓨터 구조와 프로그래밍", 조너선 스타인하트