[자료구조] 파이썬 자료구조_첫 단계

9e0na·2023년 4월 17일
data structurepython
2

[자료구조]

목록 보기
1/7
post-thumbnail

주제: 파이썬에서 자료구조를 배우기 위한 준비 단계

파이썬과 함께하는 자료구조의 이해[개정판] pp.14-30 참고해서 내용 작성하였습니다.

1. 자료구조와 추상적 데이터타입

1.1 자료구조(Data Structure)

: 일련의 동일한 타입의 데이터를 정리하여 저장한 구성체이다.

  • 데이터를 정돈하는 목적?
    : 프로그램에서 저장하는 데이터에 대해 탐색, 삽입, 삭제 등의 연산을 효율적으로 수행하기 위함

자료구조를 설계할 때에는 데이터와 데이터에 관련된 연산들을 함께 고려해야 한다.

일상생활에서의 예해당 자료구조
그릇을 쌓아서 보관하는 것
어르신들께서 자주 보는 채널 추천		스택
마트 계산대의 줄큐
버킷 리스트리스트
영어사전사전
지도그래프
컴퓨터의 디렉토리 구조트리

1.2 추상데이터타입(ADP)

정의
: 데이터와 그 데이터에 대한 추상적인 연산들로써 구성된다. 여기서 '추상'이란 연산을 구체적으로 구현을 포함하기보다는 관련 연산을 구현하는 것이다. 즉, 시스템의 핵심적인 구조나 동작에만 집중한다는 것이다.

  • 객체: 추상 데이터 타입에 속하는 객체가 정의된다.
  • 연산: 객체들 사이의 연산이 정의된다. 이 연산은 추상 데이터 타입과 외부를 연결하는 인터페이스의 역할을 수행한다.

2. 알고리즘

정의
: 주어진 문제를 유한한 시간 내에 해결하는 단계적 절차를 의미한다.

  • 프로그램 = 자료구조 + 알고리즘

  • 관심사: '좋은' 알고리즘과 자료구조를 설계한다.

  • "좋은"의 척도
    : 알고리즘과 자료구조 작업에 소요되는 실행시간 / 기억장소 사용량

    어떤 알고리즘과 자료구조를 "좋다"고 분류하기 위해서는, 분석하기 위한 정밀한 수단이 필요하다.

2.1 알고리즘의 기술 방법 & 표기

<알고리즘의 기술 방법>

1) 영어나 한국어와 같은 자연어
: 인간이 읽기 쉽지만, 자연어를 정확하게 정의하지 않으면 의미 전달이 모호해질 수도 있다.
ex) 배열에서 최대값 찾기 알고리즘_ArrayMax(list,n)

2) 흐름도(flow chart)
: 직관적이고 이해하기 쉽지만, 복잡한 알고리즘의 경우 상당히 복잡해진다.

3) 프로그래밍 언어
: 알고리즘의 가장 정확한 기술이 가능하지만, 실제 구현 시 많은 구체적인 사항들이 알고리즘의 핵심적인 내용에 대한 이해를 방해할 수 있다.

4) 의사 코드(pseudo-code)
: 알고리즘을 설명하기 위한 고급언어를 의미한다.
-> 자연어 문장보다 더 구조적이지만, 프로그래밍 언어보다는 덜 상세하다. 이 표기법은 알고리즘을 설명하는데 선호된다.
ex) 배열의 최대값 원소 찾기

2.2 의사 코드 문법

* 문법 이해 참고 사항
- exp: 수식
- var: qustn
- arg: 매개변수
- ...: 임의의 명령문들
- [x]: x가 선택적 구문 (x가 없어도 상관 없음)
- x|y|z: x,y,z 택일
- x*는 x가 0회(없어도 상관 없음) 이상 반복 가능

1) 제어(control flow)

if(exp)...
[elseif (exp)...]*  # 0회 이상 중첩 elseif절 가능
[else...] # else 절 생략 가능

for var <- exp1 to|downto exp2 
# var의 값이 exp1에서 exp2 이를 때까지 1씩 증가(혹은 감소)하며 0회 이상 반복
	...
for each var '포함' exp 
# 집합 exp이 포함하는 각 원소 var에 대해 0회 이상 반복
	...
while (exp)
# exp이 참인 동안 0회 이상 반복
	...
do
# exp이 참인 동안 1회 이상 반복
	...
    while(exp)

주의: 들여쓰기로 범위를 정의한다.

2) 연산(arithmetic)

  • <- [치환]
  • =,ㅡ,<=,>,>= [관계 연산자]
  • &, ||, ! [논리 연산자]
  • s1<=n^2 [첨자 등 수학적 표현 허용]

3) 메소드(method) 정의, 반환, 호출

* Alg method([arg],arg]*])
: 메소드 정의

* return [exp],exp]*]
: 메소드로부터의 반환

* method([arg],arg]*]
: 메소드 호출

4) 주석(comments)

input ... # 메소드의 입력 명세
output... # 메소드의 출력 명세
{This is a comment} # 코드 내 주석

2.3 기본 연산

  • 기본연산이란?
    : 탐색, 삽입, 삭제와 같은 연산이 아닌, 데이터 간 크기 비교, 데이터 읽기 및 갱신, 숫자 계산 등과 같은 단순한 연산을 의미한다.
  • 예시
    -산술식/논리식의 평가 (EXP)
    -변수에 특정값을 치환 (ASS)
    -배열원소 접근 (IND)
    -메소드 호출 (CAL)
    -메소드로부터 반환 (RET)

2.4 기본 연산 수 세기

  • 의사코드를 조사함으로써, 알고리즘에 의해 실행되는 기본 연산의 최대 개수를 입력크기의 함수 형태로 결정할 수 있다.
Alg arrayMax(A,n) # 배열에서 최대값 찾기 알고리즘
 input array A of n integers
 output maximum element of A
 						
                        {operations  count}
1. currentMax < - A[0] 	{IND, ASS	    2} < - 1

2. for i < - 1 to n-1    {ASS, EXP		1+n} < - 2
    if (A[i]>currentMax) {IND, EXP   2(n-1)} <- 3
      currentMax <- A[i] {IND, ASS   2(n-1)} <- 4
    {increment counter i} {EXP, ASS  2(n-1)} <- 5
    
3. return current Max     {RET.           1} <- 6
						  {Total.      7n-2}
  • 1번 코드는 '<-' 치환(ASS)연산과 배열원소 접근(IND) 연산으로 2 기본 시간이 필요하다.

  • 2번코드는 for문으로, 반복문 내부에서 기본 연산들이 동작된다. 이 코드에서는 '<-'치환(ASS)연산으로 1 기본 시간이 필요하다. 그리고 평가 및 비교(EXP) 연산이 작동되는데, 1번째 인덱스부터 n-1번째 인덱스까지 반복한다. 종료되는 시점인 n번째 인덱스도 포함되기 때문에 1+n-1 = n 기본 시간이 필요하다. 즉, (1+n) 기본 시간이 필요하다는 것을 알 수 있다.

  • 3번코드는 if문으로 값을 비교한다. 먼저 A[i] 에 n-1번 반복하여 원소 접근(IND)하기 때문에 (n-1) 시간이 필요하다. 그리고 '>' 비교 연산자로 n-1번 반복하여 두 값을 비교(EXP)해주기 때문에 (n-1) 시간이 필요하다. 즉, 2(n-1) 기본 시간이 필요하다.

  • 4번코드도 마찬가지로 (n-1)번 반복하기 때문에 A[i]에 n-1번 원소 접근(IND)하고, 치환(ASS)하기 때문에 2(n-1) 기본 시간이 필요하다.

  • 5번코드는 i = i+1이라는 의미로 i <- i+1라는 의미와 같다. (n-1)번 치환(ASS)되고, increment도 (n-1)번 산술식을 비교해주기 때문에(EXP) 2(n-1) 기본 시간이 필요하다

  • 6번코드는 메소드로부터 값을 반환해 주기 때문에 1 기본 시간이 필요하다.

  • 정리하면, 2+(1+n)+2(n-1)+2(n-1)+2(n-1) = 7n-2 기본 시간이 필요하다는 것을 알 수 있다.

2.5 실행시간 추정

  • 위에서 자세하게 본 것 같이 ArrayMax는 최악의 경우 7n-2개의 기본 연산을 실행한다.
  • a = 가장 빠른 기본 연산 실행에 걸리는 시간
    b = 가장 느린 기본 연산 실행에 걸리는 시간

  • T(n)을 ArrayMax의 최악인 경우의 시간이라 하면,
    a(7n-2) <= T(n) <= b(7n-2)

  • 실행시간 T(n)은 두 개의 선형함수 사이에 있다.

    <실행시간의 증가율
    만약 하드웨어나 소프트웨어 환경을 변경하면?

    • T(n)에 상수 배수 만큼의 영향을 주지만
    • T(n)의 증가율을 변경하지는 않는다.

      즉, 선형의 증가율을 나타내는 실행시간 T(n)은 ArrayMax의 고유한 속성이다.

3. 실행시간의 분석

  • 자료구조와 알고리즘의 효율성은 실행되는 연산의 수행시간으로 측정한다.
  • 자료구조에 대한 연산 수행시간 측정 방식은 알고리즘의 성능을 측정하는 방식과 동일하다.
  • 알고리즘의 성능은 실행시간을 나타내는 시간복잡도와 알고리즘이 실행하는 동안 사용되는 메모리 공간의 크기를 나타내는 공간복잡도에 기반하여 분석할 수 있다.

3.1 시간 복잡도

  • 시간 복잡도는 수행 시간이라 부르고, 실행되는 동안에 사용된 기본적인 연산 횟수를 입력 크기의 함수로 나타낸다.
  • 대부분의 알고리즘의 수행 시간은 최악 경우 분석으로 표현한다.
  • 알고리즘의 실행시간은 대체로 입력의 크기와 함께 증가한다.

알고리즘의 수행시간은 3가지 방법으로 분석한다.

1) 최악 경우 분석 (Worst-case Analysis)
: '어떤 입력이 주어지더라도 알고리즘의 수행 시간이 얼마 이상은 넘지 않는다'라는 상한의 의미를 갖는다. 분석에 비교적 용이하고, 게임, 재정, 로봇 등의 응용에서 결정적 요소이다.

2) 평균 경우 분석(Average-case Analysis)
: 입력의 균등 분포를 가정하여 분석하는데 즉, 입력이 무작위로 주어진다고 가정한다. 종종 결정하기 어렵다.

3) 최선 경우 분석(Best-case Analysis)
: 가장 빠른 수행 시간을 분석하는 것으로 거의 사용되지 않지만 최적 알고리즘을 찾는데 사용되기도 한다.

4. 실행 시간의 점근 표기법

  • 실행시간은 알고리즘이 수행하는 기본 연산 횟수를 입력 크기에 대한 함수로 표현한다.

  • 주로 다항식으로 함수를 표현되고, 이를 입력의 크기에 대한 함수로 표현하기 위해 점근 표기법(Asymptotic Natation)을 사용한다.

다음은 3가지의 대표적인 점근 표기법이다.

1) O(Big-Oh)- 표기
: 최악의 경우

2) (Big -Omega) -표기
: 최선의 경우

3) (Theta)-표기
: 평균의 경우

4.1 Big-Oh-표기

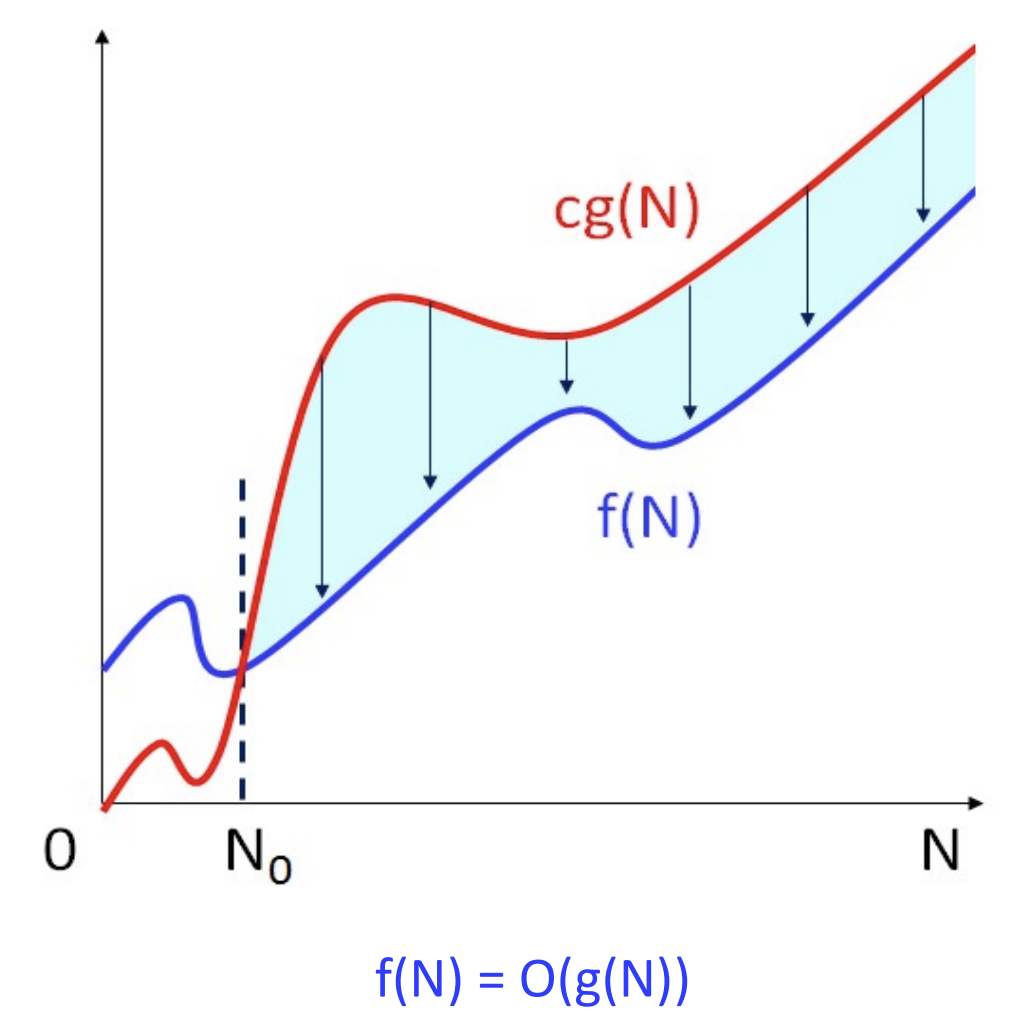
정의
: 주어진 두 개의 함수 f(N)과 g(N)에 관해, 만약 모든 N >= N에 대해서 f(N) <= cg(N)이 성립하는 양의 상수 c와 N0이 존재하면, f(N) = O(g(N))이다.

  • 주어진 수행시간의 다항식에 대해 O-표기를 찾기 위해서는 다항식에서 최고 차수 항만을 취한 뒤, 그 항의 계수를 제거 하여 g(N)을 정한다.
    ex) 5N^2+10N+3에서 최고 차수항은 5N^2이고, 여기서 계수인 5를 제거하면 N^2이다.

    5N^2+10N+3 = O(N^2)

  • 자료의 개수가 많은 경우, 차수가 가장 큰 항이 가장 영향을 크게 미치고 다른 항들은 상대적으로 무시될 수 있다는 단점이 있다.

    ex) T(n) = n^2 + n + 1

    • n=1일 때, T(n) = 1+1+1=3 (n^2항이 33.3%)
    • n=10일 때, T(n) = 100+10+1=111 (n^2항이 90%)
    • n=100일 때, T(n) = 10000+100+1=111 (n^2항이 99%)
    • n=1,000일 때, T(n) = 1000000+1000+1=1001001 (n^2항이 99%)

4.2 Big-Omega-표기

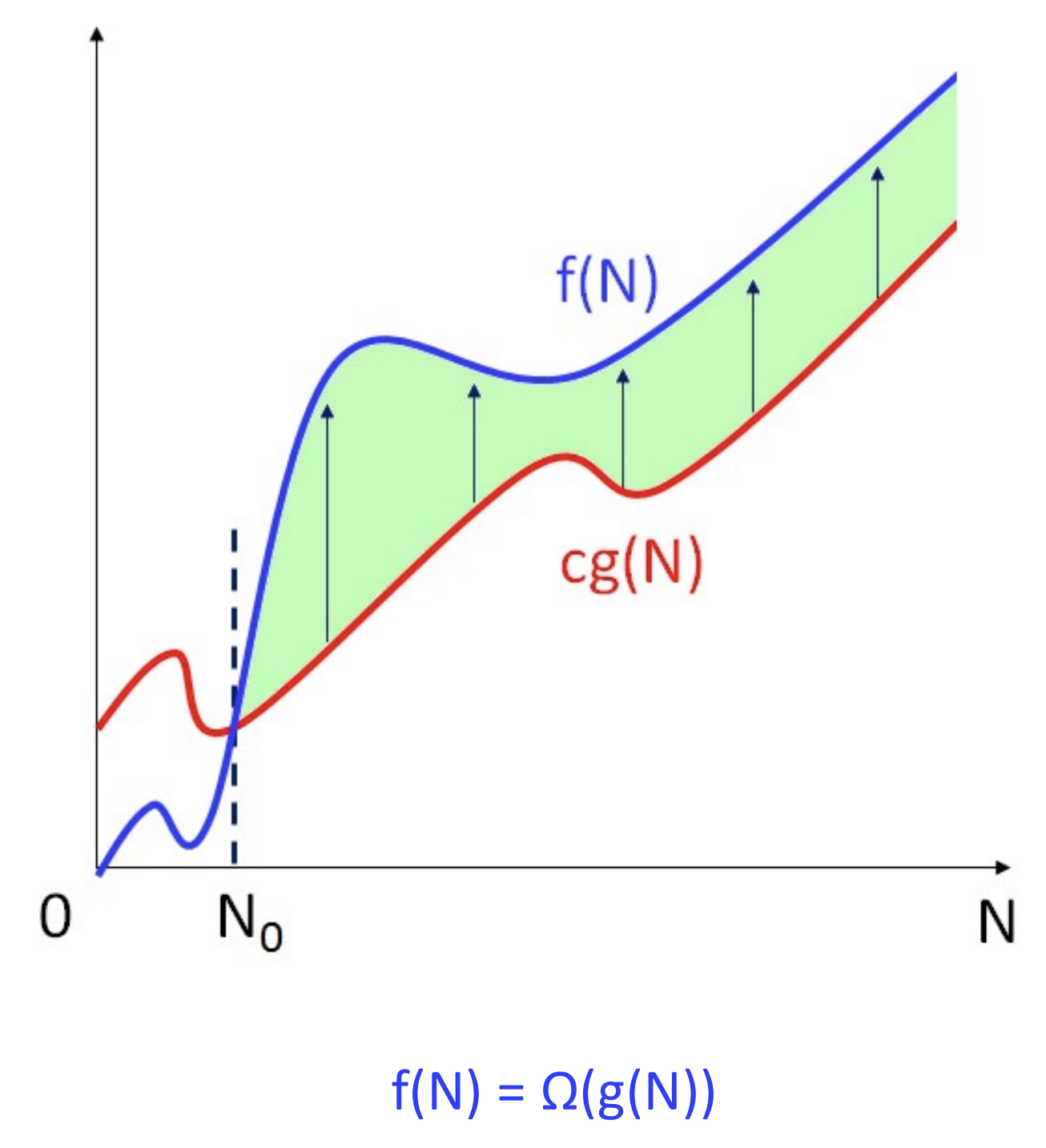
정의
: 모든 N >= N0에 대해서 f(N) >= cg(N)이 성립하는 양의 상수 c와 N0이 존재하면, f(N) = Omega(g(N))이다.

  • Omega-표기는 N0보다 큰 모든 N에 대해서 f(N)이 cg(N)보다 크다는 의미이다.

  • f(N) = Omega(g(N))은 양의 상수를 곱한 g(N)이 f(N)에 미치지 못한다는 의미이다.

  • g(N)을 f(N)의 하한(Lower Bound)이라고도 한다.

4.3 Theta-표기

정의
: 모든 N >= N0에 대해서 c1g(N) >= f(N)>=c2g(N)이 성립하는 양의 상수 c1, c2, N0가 존재하면, f(N) = Theta(g(N))이다.

  • Theta-표기는 수행시간의 Oh-표기와 Omega-표기가 동일한 겨웅에 사용한다.

  • 2N^2+3N+5 = 0h(N^2)과 동시에 Omega(N^2)이므로, 2N^2+3N+5 = Theta(N^2)

  • Theta(N^2)은 N^2과 (2N^2+3N+5)이 유사한 증가율 즉 평균 을 가지고 있다는 의미이다.

4.4 점근표기법 정리

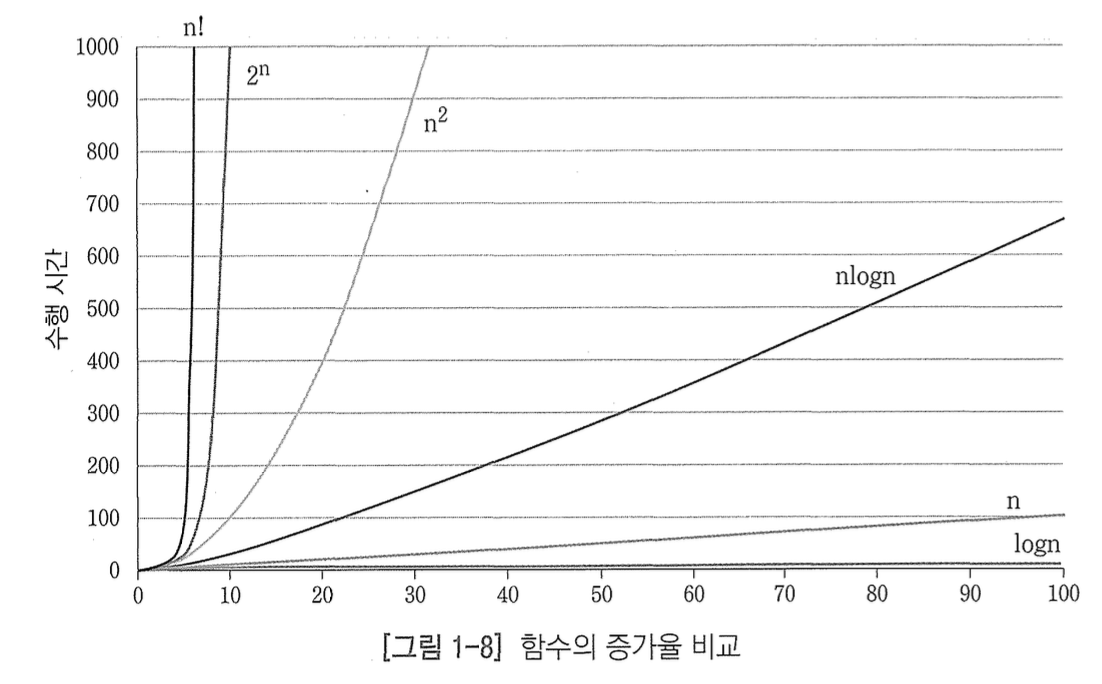
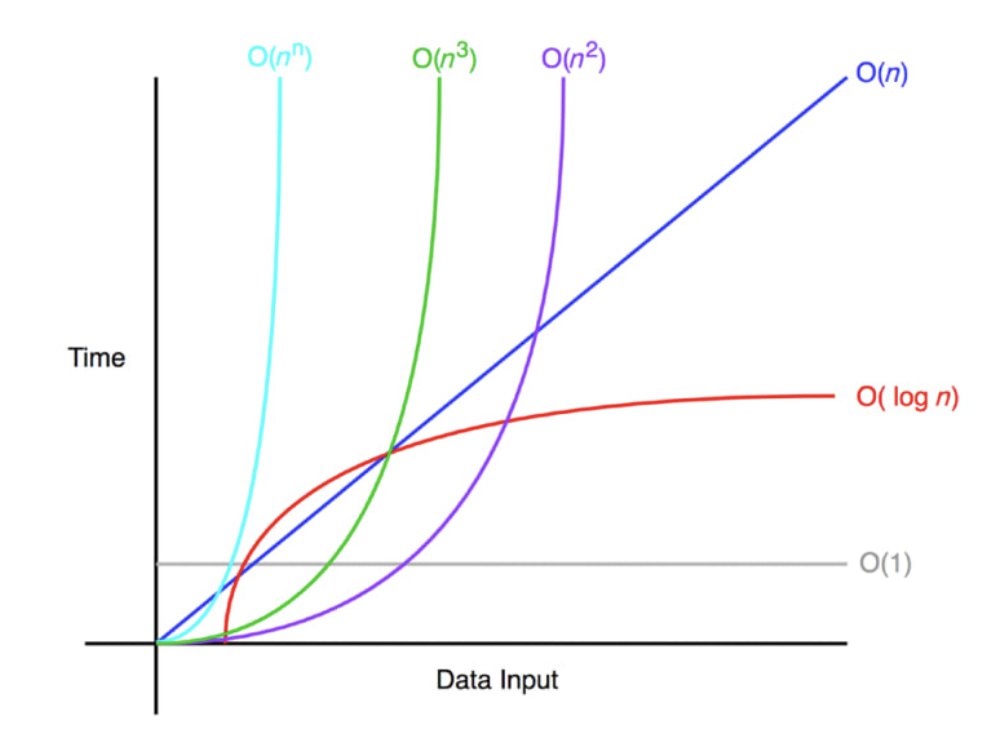
4.5 빅오 표기법의 종류

빅오 표기법종류
O(1)상수시간
O(logN)로그(대수)시간
O(N)선형시간
O(NlogN)로그선형시간
O(N^2)제곱시간
O(N^3)세제곱시간
O(2^N)지수시간
  • 밑으로 갈 수록 시간이 많이 걸리고, 비효율적이다.

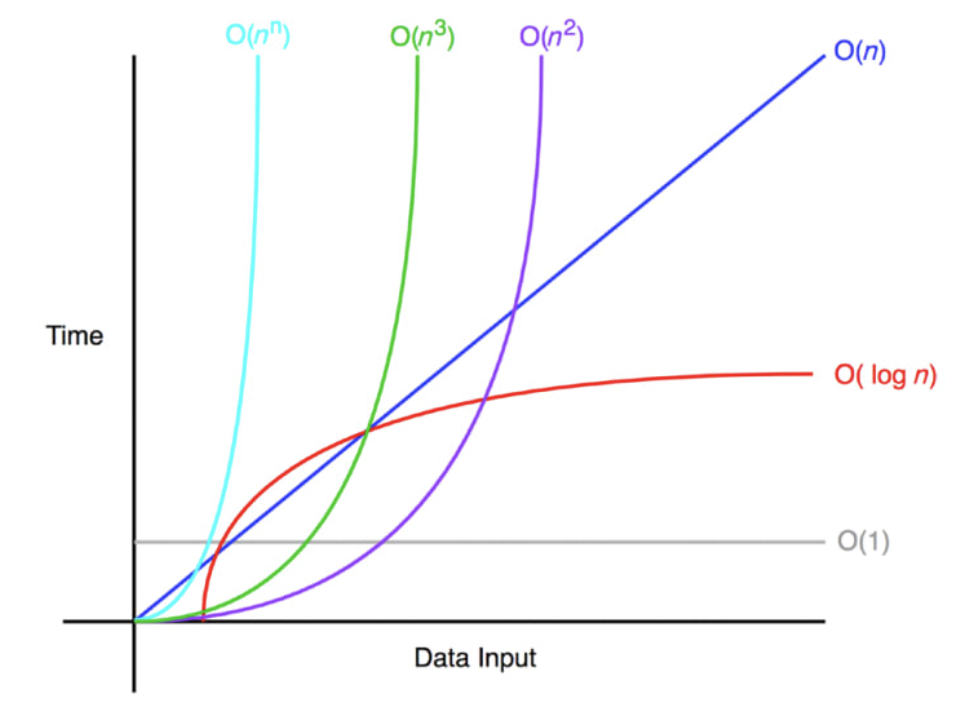
Big-O그림 출처:
DEV, Bonvic Bundi(2019.10.10.),"Understanding Big-O Notation With JavaScript",
https://dev.to/b0nbon1/understanding-big-o-notation-with-javascript-25mc (검색일: 2023.04.18.).

🎯 Summary

지금까지 실행시간과 메모리의 크기를 신경 쓰지 않고 코드를 직접 구성하고 구현했었다. 특히 지난 2학기 머신러닝 컴피티션에서 자료구조를 신경 쓰지 않고 코드를 구성하다보니 코드의 실행시간이 오래 걸렸고, 비효율적인 느낌을 너무 많이 받았었다. 그렇기 때문에 나에게 있어서 자료구조 공부는 너무 필요하였다.

초반 내용 중 '기본 연산 수 세기'부분이 살짝 이해가 안됐다. '이게 이러한 과정을 통해서 동작되는건가?'생각하며 이해한 내용을 기술하였다. 또한, 알고리즘은 대부분 최악의 경우를 생각하며 코드를 구성해야 되는 점을 알게 되었다. 많은 표기법이 있었지만, 여러 번 복습함으로써 내것으로 만들어야겠다.

자료구조 공부 1일차지만 너무 재밌다. 말로만 듣던 스택과 큐 구현하는 날까지 열심히 공부해야겠다!

📚 References

profile
9e0na
디지털 마케터가 되기 위해 [a-zA-Z]까지 정리하는 거나입니다 😊
다음 포스트

[자료구조] 재귀 알고리즘

0개의 댓글