주제: 파이썬에서 큐 구현하기

파이썬과 함께하는 자료구조의 이해[개정판] pp.101-104 참고해서 내용 작성하였습니다.
파이썬으로 배우는 자료구조 핵심 원리 pp.74-77 참고해서 내용 작성하였습니다.

1. 덱(DEQUE)

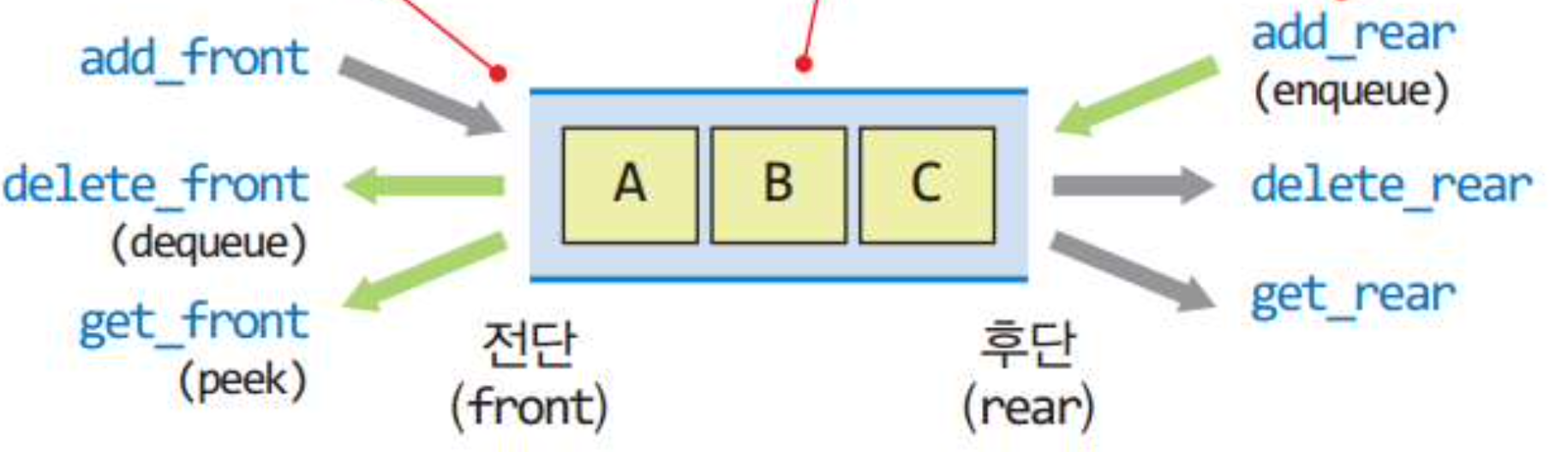
정의
양쪽 끝에서 삽입과 삭제를 허용하는 자료구조이다.

• 특징
  -스택과 큐 자료구조를 혼합한 자료구조
  -스택이나 큐보다 입출력이 자유로운 자료구조
  -덱은 double-ended queue의 줄임말
  -전단(front)와 후단(rear)에서 모두 삽입과 삭제가 가능한 큐
  -하지만 여전히 중간에 넣거나 빼지는 못함
  -큐나 스택과 비슷한 연산들이 많음
  -스크롤(Scroll), 문서 편집기 등의 undo연산, 웹 브라우저의 방목 기록 등에 사용됨
  -파이썬의 리스트나 이중연결리스트로 구현 가능

단순연결리스트보다 이중연결리스트에 적합한 이유는?

: rear가 가리키는 노드의 이전 노드의 레퍼런스를 알아야 삭제가 가능하기 때문에 이중연결리스트가 적합하다.

• 덱 ADT

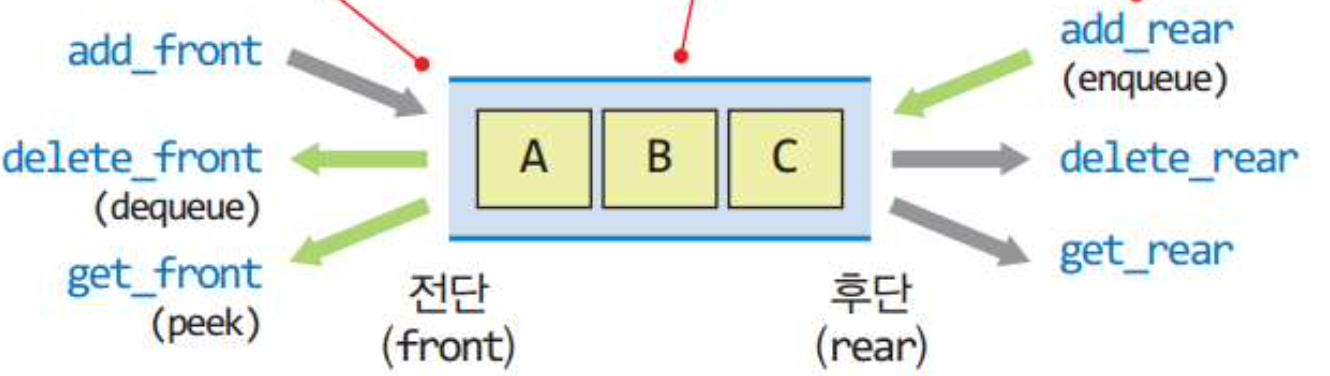
데이터: 전단과 후단을 통한 접근을 허용하는 항목들의 모음

• Deque(): 비어 있는 새로운 덱을 생성
• isEmpty(): 덱이 비어있으면 True를 아니면 False 반환
• addFront(x): 항목x를 덱의 맨 앞에 추가
• deleteFront(): 맨 앞의 항목을 꺼내서 반환
• getFront(): 맨 앞의 항목을 꺼내지 않고 반환
• addRear(x): 항목 x를 덱의 맨 뒤에 추가
• deleteRear(): 맨 뒤의 항목을 꺼내서 반환
• getRear(): 맨 뒤의 항목을 꺼내지 않고 반환
• isFull(): 덱이 가득 차 있으면 True를 아니면 False 반환
• size(): 덱의 모든 항목들의 개수 반환
• clear(): 덱을 공백상태로 만듬

---

1.1 원형 덱의 연산

1) 큐와 알고리즘이 동일한 연산

• addRear(), deleteFront(), getFront()
  = 큐의 enqueue, dequeue, peek 연산과 동일
• 덱의 후단을 스택의 상단으로 사용하면,
  addRear(), deleteRear(), getRear()
  = 스택의 push, pop, peek 연산과 동일

2) 큐와 데이터가 동일하고 연산도 유사함

3) 원형 큐에서 추가된 연산

• delete_rear(), add_front(), get_rear()
  = 반 시계방향 회전 필요

front <- (front -1 + MAX_QSIZE) % MAX_QSIZE
rear <- (rear -1 + MAX_QSIZE) % MAX_QSIZE

---

2. 덱의 구현

1) 원형 큐를 상속하여 원형 덱 클래스를 구현

class CircularDeque(CircularQueue) #CircularQueue에서 상속

2) 덱의 생성자 (상속되지 않는다)

def __init___(self): # CircularDeque의 생성자
	super().__init__() # 부모 클래스의 생성자를 호출

• front,rear,items와 같은 변수는 추가로 선언X
• 자식클래스에서 부모를 부르는 함수가 super()

3) 재 사용: isEmpty, isFull, size, clear

4) 인터페이스 변경

def addRear(self, item):self.enqueue(item) # enqueue호출
def deleteFront(self): return self.dequeue() # 반환에 주의
def getFront(self): return self.peek() 

---

2.1 Collections 패키지를 활용한 덱의 구현

🤜 입력

from collections import deque
dq = deque('data')  #  새 데크 객체를 생성
for elem in dq:
    print(elem.upper(), end='')
print()
dq.append('r')  # 맨 뒤와
dq.appendleft('k')  # 맨 앞에 항목 삽입
print(dq)
dq.pop()  # 맨 뒤와
dq.popleft()  # 맨 앞의 항목 삭제
print(dq[-1]) # 맨 뒤의 항목 출력
print('x' in dq)
dq.extend('structure')  # 맨 뒤와 
dq.extendleft(reversed('python')) # 맨 앞에 여러 항목 삽입 
print(dq)

💻 출력

DATA
deque(['k', 'd', 'a', 't', 'a', 'r'])
a
False
deque(['p', 'y', 't', 'h', 'o', 'n', 'd', 'a', 't', 'a', 's', 't', 'r', 'u', 'c', 't', 'u', 'r', 'e'])
1

---

2.2 원형 덱의 구현

🤜 입력

def addFront(self, item):  # 새로운 기능: 전단 삽입
    if not self.isFull():
        self.items[self.front] = item # 항목 저장
        self.front = self.front -1 # 반시계 방향으로 회전
        if self.front <0: self.front = MAX_QSIZE -1
            
def deleteRear(self): # 새로운 기능: 후단 삭제
    if not self.isEmpty():
        item = self.items[self.rear]; # 항목 복사
        self.rear = self.rear -1  # 반시계 방향으로 회전
        if self.rear <0: self.rear = MAX_QSIZE -1
        return item # 항목 반환
    
def getRear(self):  # 새로운 기능: 후단 peek
    return self.items[self.rear]

---

3. 이중연결리스트의 응용: 연결된 덱

---

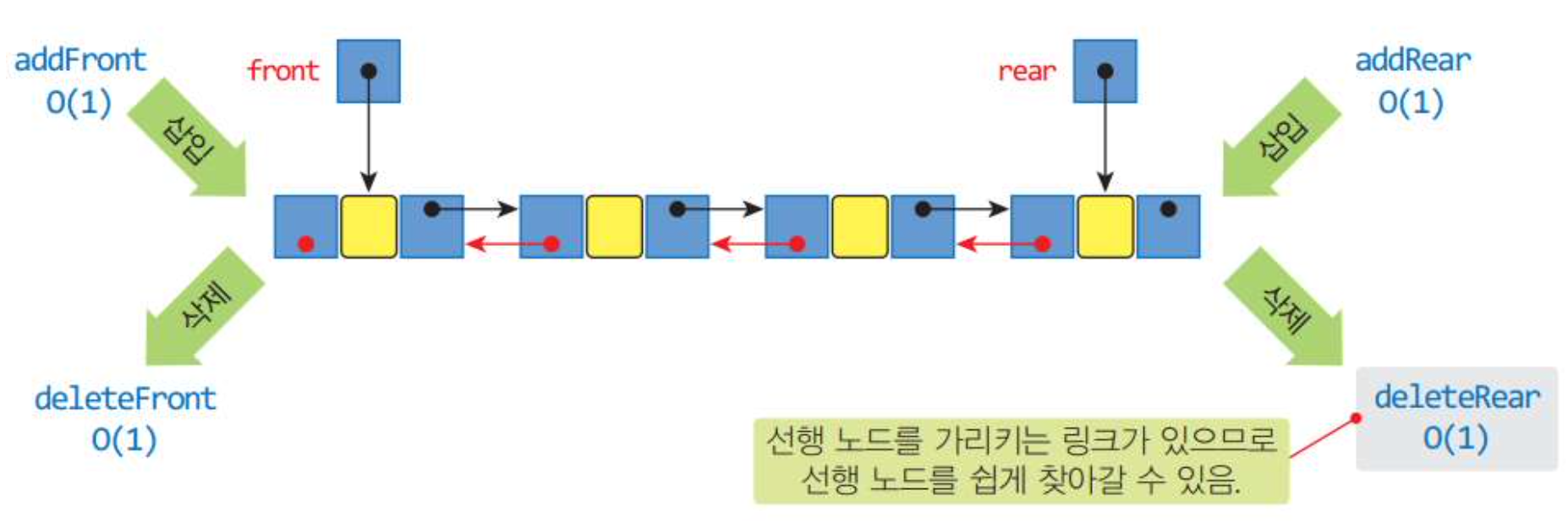
3.1 이중연결리스트로 구현한 덱 문제 풀기

🎲 주의 : 연산 수행 도중 원소가 모두 삭제되어 데크가 비는 경우에도, 초기화 상태가 되어야 한다
🎯 위의 그림과 같이 입력을 하면, 출력의 결과가 위와 같아야 한다.

💻 입출력 형식:
1) 첫 번째 라인 : 연산의 개수 n
2) 두 번째 이후 라인: n개의 연산이 한 줄에 하나씩 차례로 입력됨.
- 하나의 줄에는 연산의 종류, 추가인 경우 원소가 주어짐 (원소는 양의 정수로 표기). 
- 연산의 종류: 다음의 연산 이름이 대문자로 주어짐.
* AF (add_front),
* AR (add_rear), 
* DF (delete_front), 
* DR (delete_rear), 
* P (print_depue) 
* underflow 발생 시, 화면에 underflow를 출력하고 프로그램 종료.

---

3.2 이중연결리스트를 위한 노드

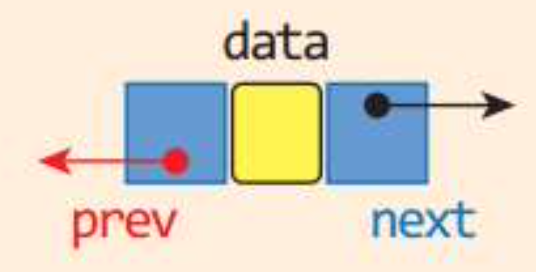
class DNode: # 이중연결리스트를 위한 노드
            def __init__(self, elem, prev = None, next = None):
                self.data = elem
                self.prev = prev
                self.next = next

---

3.3 연결된 덱 클래스

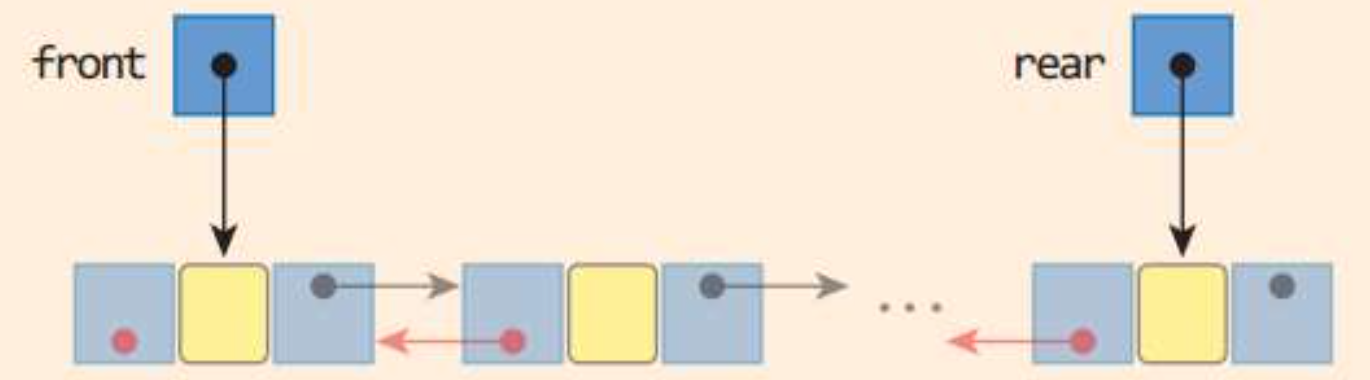
class DoublyLinkedDeque<:
	def __init__(self):
            self.front = None
            self.rear = None

        def isEmpty(self): return self.front == None
        def clear(self): self.front = self.front = None 

---

3.4 add_front(), add_rear()

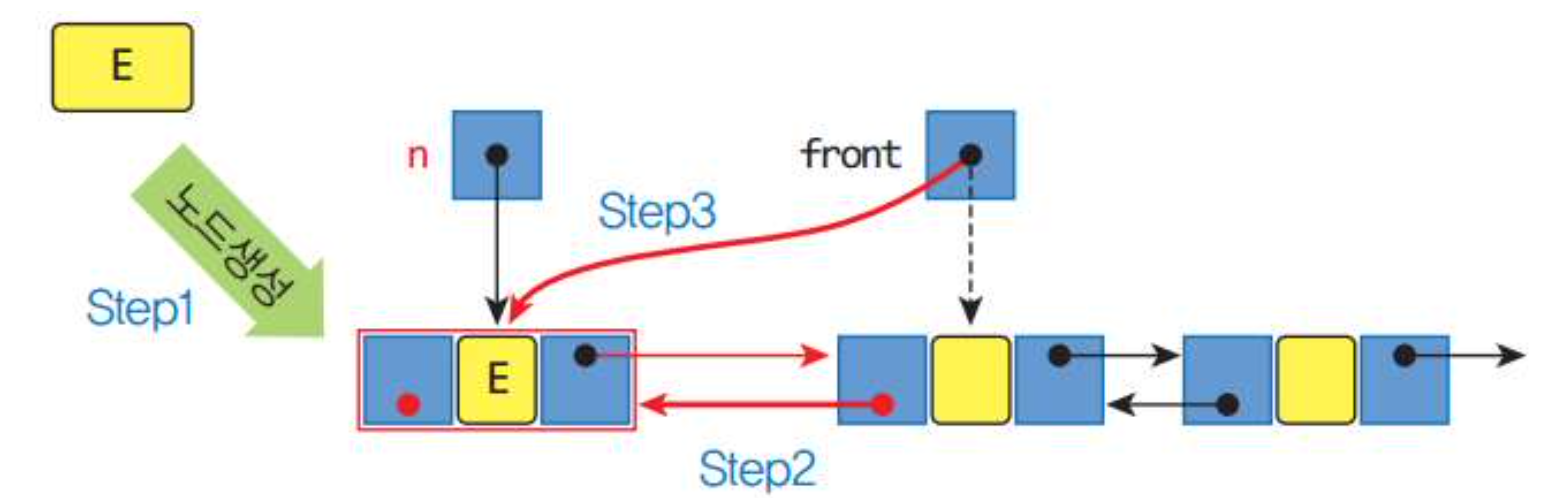
def add_front(self, item): 
            node = self.DNode(item, None, self.front)  # Step1
            if (self.isEmpty()): # 공백이면
                self.front = self.rear = node  # front와 rear 모두 node
            else:  # 공백이 아니면
                self.front.prev = node # Step2
                self.front = node # Step3

        def add_rear(self, item):
            node = self.DNode(item, self.rear, None) # Step1
            if (self.isEmpty()): # 공백이면
                self.front = self.rear = node  # front와 rear 모두 node
            else:  # 공백이 아니면
                self.rear.next = node # Step2
                self.rear = node # Step3

---

3.5 delete_front(), delete_rear()

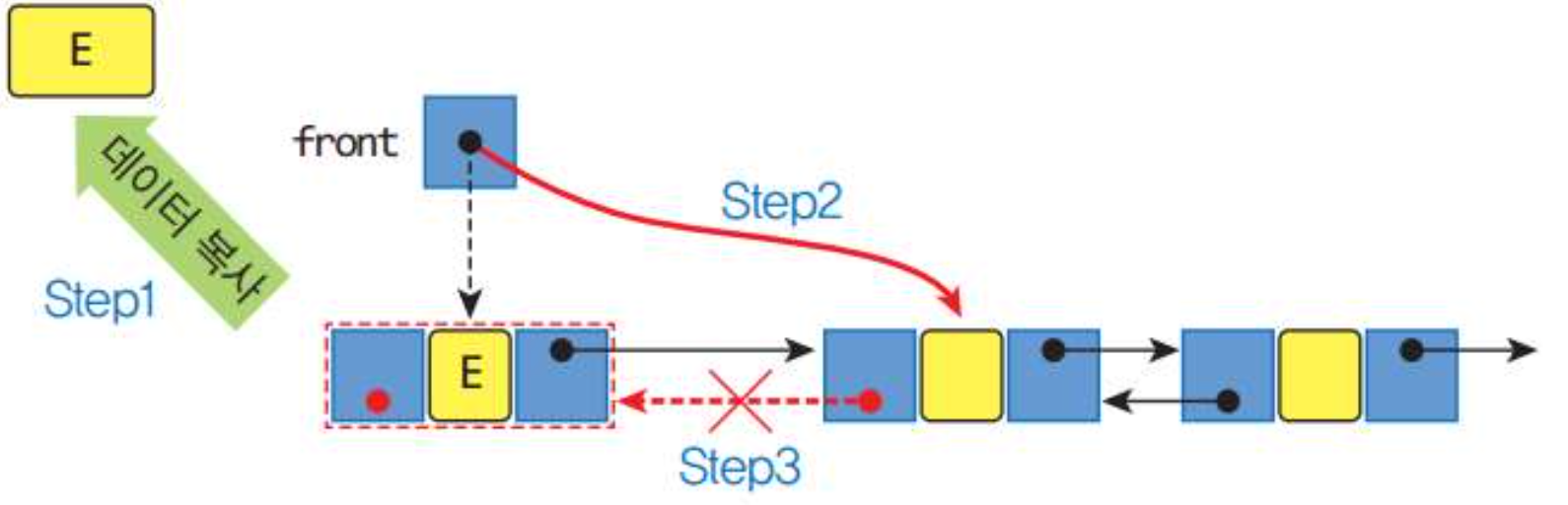
def delete_front(self):
            if not self.isEmpty():
                data = self.front.data
                self.front = self.front.next
                if self.front == None:
                    self.rear = None
                else:
                    self.front.prev = None  # Step3
                return data    # Step4
            
        def delete_rear(self):
            if not self.isEmpty():  
                data = self.rear.data  # Step1 # 데이터 복사
                self.rear = self.rear.prev  # Step2
                if self.rear == None:  # 노드가 하나 뿐이면
                    self.front=None  # front도 None으로 설정
                else:
                    self.rear.next = None  # Step3
                return data  # Step4

---

3.6 총 정리

🤜 입력

class DoublyLinkedDeque:
        class DNode:
            def __init__(self, elem, prev = None, next = None):
                self.data = elem
                self.prev = prev
                self.next = next

        def __init__(self):
            self.front = None
            self.rear = None

        def isEmpty(self): return self.front == None
        def clear(self): self.front = self.front = None 

        def size(self):
            node = self.front
            count = 0
            while not node == None:
                node = node.next
                count += 1
            return count

        def print_deque(self):
            print(end='') 
            node = self.front
            while node.next != None:
                print(f"{node.data}", end=' ')
                node = node.next
            print(f"{node.data}")

        def add_front(self, item):
            node = self.DNode(item, None, self.front)
            if (self.isEmpty()):
                self.front = self.rear = node
            else:
                self.front.prev = node
                self.front = node

        def add_rear(self, item):
            node = self.DNode(item, self.rear, None)
            if (self.isEmpty()):
                self.front = self.rear = node
            else:
                self.rear.next = node
                self.rear = node

        def delete_front(self):
            if not self.isEmpty():
                data = self.front.data
                self.front = self.front.next
                if self.front == None:
                    self.rear = None
                else:
                    self.front.prev = None
                return data
            
        def delete_rear(self):
            if not self.isEmpty():
                data = self.rear.data
                self.rear = self.rear.prev
                if self.rear == None:
                    self.front=None
                else:
                    self.rear.next = None
                return data
          
            
            
if __name__ == "__main__":
    num = int(input())
    Deque = DoublyLinkedDeque()
    for i in range(num):
        inputs = input().split(" ")
        operation = inputs[0]
        if operation == "AF":
            number = inputs[-1]
            Deque.add_front(number)
        elif operation == "AR":
            number = inputs[-1]
            Deque.add_rear(number)
        elif operation == "DF":
            data = Deque.delete_front()
            if data is None:
                print('underflow')
                break
        elif operation == 'DR':
            data = Deque.delete_rear()
            if data is None:
                print('underflow')
                break
        elif operation == 'P':
            Deque.print_deque()

💻 출력

15
AF 10
AF 20
AF 30
AR 40
AR 50
P
30 20 10 40 50
DF
DF
DR
P
10 40
DF
DR
DR
underflow

---

4. 수행시간

파이썬 공식 문서를 확인하면 deque 파트에 다음 문장이 있다.

"Indexed access is 0(1) at both ends b니t slows to O(n) in the middle."

즉, "인덱스로 양 끝에 접근할 때는 빅오가 O(1)이지만 중간에 있는 데이터에 접근하려면 조금 느려서 빅오가 O(n)이다."

---

🎯 Summary

이중연결리스트를 활용하여 덱을 구현해보았다. 그림을 보면서 이해를 하니 이해하기 수월했다. 위의 이중연결리스트 문제를 구현 할 때, underflow가 출력이 안돼서 고생을 했다. 사실 for문 안에 data라는 변수를 추가해서 이 데이터가 없더라면 underflow를 출력하고, break를 걸었으면 되는 간단한 문제였다. 아직 파이썬에 대해서 많이 많이 부족하다.. 철저히 복습과 예습을 병행해야겠다.

📚 References

• 양성봉(2022),'파이썬과 함께하는 자료구조의 이해[개정판]', 생능출판, pp.101-104.
• 양태환(2021),'파이썬으로 배우는 자료구조 핵심 원리', 길벗, pp.74-77.
• 덱 그림 출처: https://commons.wikimedia.org/wiki/File:Deque.svg