0423 기초수학 4일차(~40)

등차수열

일반항, n번째항, n번째항까지의 합

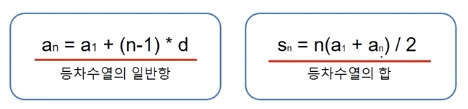
공식없이 파이썬으로 하기

inputA1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0; sumN = 0;
n=1
while n<= inputN:
    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('{}번째 항의 값: {}'.format(n,valueN))
        print('{}번째 항까지의 합 : {}'.format(n,sumN))
        n +=1
        continue

    valueN += inputD
    sumN += valueN
    print('{}번째 항의 값: {}'.format(n, valueN))
    print('{}번째 항까지의 합 : {}'.format(n, sumN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합 : {}'.format(inputN, sumN))

공식으로 하기

#공식 : an +(n-1)*d
valueN = inputA1 + (inputN-1)*inputD
print('{}번째 항의 값 : {}'.format(inputN,valueN))

#sn = n(a1+an) /2
sumN = inputN * (inputA1*valueN) / 2
print('{}번째 항까지의 합 : {}'.format(inputN,int(sumN)))

등비수열

일반항, n번째항, n번째항까지의 합

공식없이 파이썬으로 하기

inputA1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0; sumN = 0;

n=1
while n<= inputN:
    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('{}번째 항의 값: {}'.format(n,valueN))
        print('{}번째 항까지의 합 : {}'.format(n,sumN))
        n +=1
        continue

    valueN *= inputR
    sumN += valueN
    print('{}번째 항의 값: {}'.format(n, valueN))
    print('{}번째 항까지의 합 : {}'.format(n, sumN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합 : {}'.format(inputN, sumN))

공식사용

#an = a1 *r^(n-1)
valueN = inputA1 *(inputR**(inputN-1))
print('{}번째 항의 값: {}'.format(inputN, valueN))
#sn = a1 * (1-r^n)/(1-r)
sumN = inputA1*(1-(inputR**inputN)) / (1-inputR)
print('{}번째 항까지의 합 : {}'.format(inputN, int(sumN)))

시그마

시그마 : 수열의 합

inputA1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0; sumN = 0;
n=1

while n <= inputN:
    if n ==1:
        valueN = inputA1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n,sumN))
        n+=1
        continue
    valueN *= inputR
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1
print('{}번째 항까지의 합: {}'.format(inputN, format(sumN,',')))

계차수열

계차수열 : 두항의 차로 이루어진 수열

inputAN = int(input('an 입력: '))
inputAN1 = int(input('a1 입력: '))
inputBN1 = int(input('b1 입력: '))
inputBD = int(input('bn 공차 입력: '))

valueAN = 0
valueBN = 0

n=1

while n <= inputAN:
    if n ==1:
        valueAN = inputAN1
        valueBN = inputBN1
        print('an의 {}번째 항의 값 : {}'.format(n,valueAN))
        print('bn의 {}번째 항의 값 : {}'.format(n,valueBN))
        n +=1
        continue

    valueAN = valueAN + valueBN
    valueBN = valueBN + inputBD
    print('an의 {}번째 항의 값 : {}'.format(n, valueAN))
    print('bn의 {}번째 항의 값 : {}'.format(n, valueBN))
    n +=1
print('an의 {}번째 항의 값 : {}'.format(inputAN, valueAN))
print('bn의 {}번째 항의 값 : {}'.format(inputAN, valueBN))


#an = {2,5,11,20,32,47,65,86,110,137,167}
#bn = { 3,6,9,12,15,18,21,24,27,30 }
#계차수열 시그마 이용해서 an 구하기
#bn의 n-1까지의 시그마값은 an-a1값과 동일
#bn의 일반항 : 3+(n-1)*3= 3n    /bn의 n-1까지의 시그마 : (n-1)(3+3(n-1))/2
#시그마 값 : (n-1)3n/2 = (3n^-3n)/2 = an-2
#따라서 an = (3n^-3n)+4/2

valueAN = ((3*inputAN **2 - 3*inputAN)+4) /2
print('an의 {}번째 항의 값 : {}'.format(inputAN, int(valueAN)))

피보나치 수열

inputN = int(input('n 입력: '))

valueN = 0
sumN = 0

valuePreN2=0
valuePreN1=0

n=1
while n <= inputN:
    if n ==1 or n == 2:
        valueN = 1
        valuePreN2 = valueN
        valuePreN1 = valueN
        sumN += valueN
        n +=1

    else:
        valueN = valuePreN2 + valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        sumN += valueN
        n +=1

print('{}번째 항의 값 : {}'.format(inputN,valueN))
print('{}번째 항까지의 합 : {}'.format(inputN,sumN))