[Baekjoon / Python] 1766번 : 문제집

loveydev·2023년 5월 11일

Graph Python3 Topology Sort priority queue

Baekjoon

목록 보기

3/8

개요

🖱️ 문제 링크 : https://www.acmicpc.net/problem/1766

시간 제한 : 2초

메모리 제한 : 128 MB

문제

⌨️ 입력

첫째 줄에 문제의 수 N(1 ≤ N ≤ 32,000)과 먼저 푸는 것이 좋은 문제에 대한 정보의 개수 M(1 ≤ M ≤ 100,000)이 주어진다.

둘째 줄부터 M개의 줄에 걸쳐 두 정수의 순서쌍 A,B가 빈칸을 사이에 두고 주어진다. 이는 A번 문제는 B번 문제보다 먼저 푸는 것이 좋다는 의미이다.

항상 문제를 모두 풀 수 있는 경우만 입력으로 주어진다.

🖨️ 출력

첫째 줄에 문제 번호를 나타내는 1 이상 N 이하의 정수들을 민오가 풀어야 하는 순서대로 빈칸을 사이에 두고 출력한다.

해결 방법

💡 문제 이해

위상정렬(Typology sort) + 우선순위 큐(Priority Queue) 문제 였다.

이전에 위상정렬을 공부했던 터라 이해하는데 크게 어려움은 없었다.
다만, 다음 조건으로 인해 기존의 위상정렬과는 다른 점이 있었다.

위 문제 예시의 경우 2번 문제를 풀기 전에 4번 문제를 반드시 먼저 풀어야 한다.
1번 문제를 풀기 전에 3번 문제를 반드시 먼저 풀어야 한다.
→ 선수 관계가 있구나! (위상 정렬)

하지만, 가능하면 쉬운 문제부터 풀어야 한다.
→ 문제가 난이도 순서대로 정렬되어 있으므로, 진입차수가 0으로 동일하다면 문제번호가 작은 순서대로 풀어야 한다! (우선순위 큐 이용)

2번째 조건으로 인해서 매번 큐에서 POP 되는 원소는 최소값이어야 한다.

📖 위상정렬

순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘.
ex) 선수과목을 고려한 학습 순서

큐를 이용하는 위상 정렬 알고리즘의 동작 과정 은 다음과 같다.

진입차수가 0인 모든 노드를 큐에 넣는다.
큐가 빌 때까지 다음의 과정을 반복한다.

큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
새롭게 진입차수가 0이 된 노드를 큐에 넣는다.

🔧 위상 정렬의 특징

위상 정렬은 순환하지 않는 방향 그래프에 대해서만 수행할 수 있다.
위상 정렬에서는 여러가지 답이 존재할 수 있다. (한 단계에서 큐에 원소가 2개 이상 들어가는 경우)
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다.

🚥 우선순위 큐

큐 (Queue) 는 먼저 들어오는 데이터가 먼저 나가는 선입선출(FIFO) 구조 이다.
하지만 우선순위 큐 (Priority Queue) 는 먼저 들어오는 데이터가 아니라, 우선순위가 높은 데이터가 먼저 나가는 형태의 자료구조이다.

파이썬에서 일반적으로 우선순위 큐는 Heap(힙) 을 이용하여 구현한다.
파이썬의 heapq 모듈은 최소 힙 구조(Min Heap) 로 구현되어 있다.

🚦 힙

힙 (Heap) 은 우선순위 큐를 위해 고안된 완전이진트리 (Complete Binary Tree) 형태의 자료구조이다.
여러개의 값 중 최댓값 또는 최솟값을 찾아내는 연산이 매우 빠르다.

힙의 특징
- 완전이진트리 (Complete BT) 형태로 이루어져 있다.
- 부모노드와 서브트리간 대소관계가 성립된다. (반 정렬 상태)
- 이진검색트리 (BST) 와 달리 중복된 값이 허용된다.
힙의 종류
- 최소 힙 (Min Heap) : 부모노드의 키 값이 자식노드보다 작거나 같은 완전이진트리
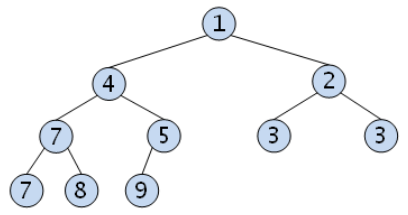
- 최대 힙 (Max Heap) : 부모노드의 키 값이 자식노드보다 크거나 같은 완전이진트리

Python Code

# 백준 1766 문제집
# 위상 정렬과 우선순위 큐
import sys
import heapq
read = sys.stdin.readline

def topology_sort():
    queue = []

    # 진입 차수가 0인 모든 노드를 큐에 넣음
    for i in range(1,N+1):
        if indegree[i] == 0:
            # 진입 차수가 동일하게 0이더라도 문제번호가 작은 순서대로 풀어야 하므로, 최소 힙 이용
            heapq.heappush(queue,i)

    while queue:
        current = heapq.heappop(queue)
        print(current, end =' ')
        
        for next in graph[current]:
            indegree[next] -= 1
            
            # 현재 노드로 인해 다음 노드의 진입차수가 0이 된 경우 우선순위를 가짐.
            if indegree[next] == 0:
                heapq.heappush(queue,next)

# 문제의 수, 먼저 푸는것이 좋은 문제에 대한 정보의 개수
N,M = map(int,read().split())
indegree = [0] * (N+1)
graph = [ [] for _ in range(N+1) ]

for _ in range(M):
    # a를 b보다 먼저 풀어야 함.
    a,b = map(int,read().split())
    graph[a].append(b)
    indegree[b] += 1

topology_sort()