
개요
🖱️ 문제 링크 : https://www.acmicpc.net/problem/14938
- 시간 제한 : 1초
- 메모리 제한 : 128 MB
- 기출 : University > 서강대학교 > 2017 Sogang Programming Contest > Master D번
문제
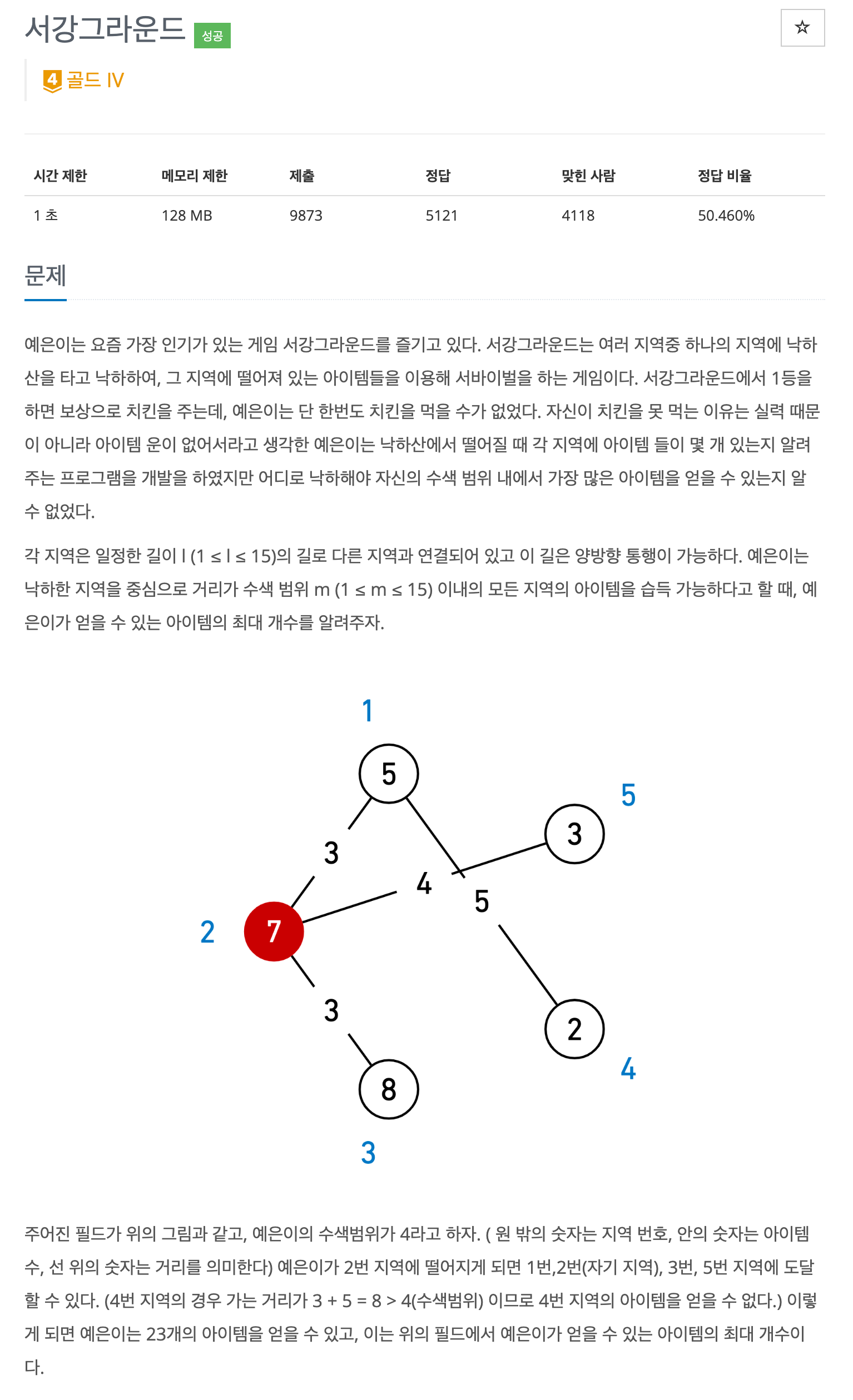
⌨️ 입력
첫째 줄에는 지역의 개수 n (1 ≤ n ≤ 100)과 예은이의 수색범위 m (1 ≤ m ≤ 15), 길의 개수 r (1 ≤ r ≤ 100)이 주어진다.
둘째 줄에는 n개의 숫자가 차례대로 각 구역에 있는 아이템의 수 t (1 ≤ t ≤ 30)를 알려준다.
세 번째 줄부터 r+2번째 줄 까지 길 양 끝에 존재하는 지역의 번호 a, b, 그리고 길의 길이 l (1 ≤ l ≤ 15)가 주어진다.
🖨️ 출력
예은이가 얻을 수 있는 최대 아이템 개수를 출력한다.
해결 방법
💡 문제 이해
배틀 그라운드 패러디인가?
예은이는 낙하산에서 떨어질 때 각 지역에 아이템 들이 몇 개 있는지 알려주는 프로그램을 개발을 하였지만 어디로 낙하해야 자신의 수색 범위 내에서 가장 많은 아이템을 얻을 수 있는지 알 수 없었다.
아무튼 해당 게임에서 어디로 낙하하느냐에 따라서 파밍할 수 있는 아이템의 개수가 다르므로 최대 파밍을 할 수 있는 지점을 찾는 문제이다.
해당 게임을 알고 있던 터라 나름 재밌게 읽은 문제이다!
문제의 핵심은 예은이가 어디에 낙하할지 모른다 이다.
그리고 각 간선들은 무방향이라는 점!
이게 무슨 소리냐 하면 어디에 낙하하는지(정점)에 따라서 다른 정점으로 가는 최소비용이 달라지기 때문이다.
다익스트라 알고리즘을 이용해서 예은이를 각 정점에 낙하 시키고, 그 정점으로 부터 다른 나머지 정점들에 대한 최소비용을 찾는다 -> 예은이의 수색범위 내에 있는 정점들을 추려내서 해당 정점에 있는 아이템 수를 get_item에 더해준다.
get_item 에 저장된 내용들은 result에 저장해두고, 예은이를 모든 정점에 낙하시킨 후에 result에서 가장 큰 값을 출력하면 끝.
Python Code
# 백준 14938 서강 그라운드
import sys
import heapq
read = sys.stdin.readline
INF = int(2e9)
# 지역의 개수, 수색 범위, 길의 개수
v, limit, e = map(int, read().split())
items = [0] + list(map(int,read().split()))
graph = [ [] for _ in range(v+1) ]
for _ in range(e):
a,b,length = map(int, read().split())
graph[a].append([b, length])
graph[b].append([a, length])
def dijkstra(start):
queue = []
distance = [INF]*(v+1)
# 자기 자신으로 가는 비용은 0
distance[start] = 0
heapq.heappush(queue, [0, start])
while queue:
dist, current_node = heapq.heappop(queue)
if distance[current_node] < dist:
continue
for next_node, next_cost in graph[current_node]:
cost = dist + next_cost
if distance[next_node] > cost:
distance[next_node] = cost
heapq.heappush(queue, [cost, next_node])
return distance
result = []
for i in range(1, v+1):
temp = dijkstra(i)
get_item = 0
for j in range(1, v+1):
# 수색 범위 내이면
if temp[j] <= limit:
get_item += items[j]
result.append(get_item)
print(max(result))