
개요
🖱️ 문제 링크 : https://www.acmicpc.net/problem/1005
- 시간 제한 : 1초
- 메모리 제한 : 512 MB
문제
⌨️ 입력
첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부터 N번까지 존재한다.)
둘째 줄에는 각 건물당 건설에 걸리는 시간 D1, D2, ..., DN이 공백을 사이로 주어진다. 셋째 줄부터 K+2줄까지 건설순서 X Y가 주어진다. (이는 건물 X를 지은 다음에 건물 Y를 짓는 것이 가능하다는 의미이다.)
마지막 줄에는 백준이가 승리하기 위해 건설해야 할 건물의 번호 W가 주어진다.
🖨️ 출력
건물 W를 건설완료 하는데 드는 최소 시간을 출력한다. 편의상 건물을 짓는 명령을 내리는 데는 시간이 소요되지 않는다고 가정한다.
건설순서는 모든 건물이 건설 가능하도록 주어진다.
해결 방법
💡 문제 이해
자료구조 시간에 언젠가 한번쯤 들은거 같은 위상정렬(Typology sort) 문제 였다.
거기에 추가적으로 목표 지점까지의 누적 비용을 구하기 위해서 DP의 메모이제이션 기법을 활용한다.
사실 위상정렬을 들어보기만 했지 코드로 써본적이 단 한번도 없어서 그냥 시작부터 답지 봤다.
정답이 목적이 아닌 개념 공부를 위한 문제풀이였다.
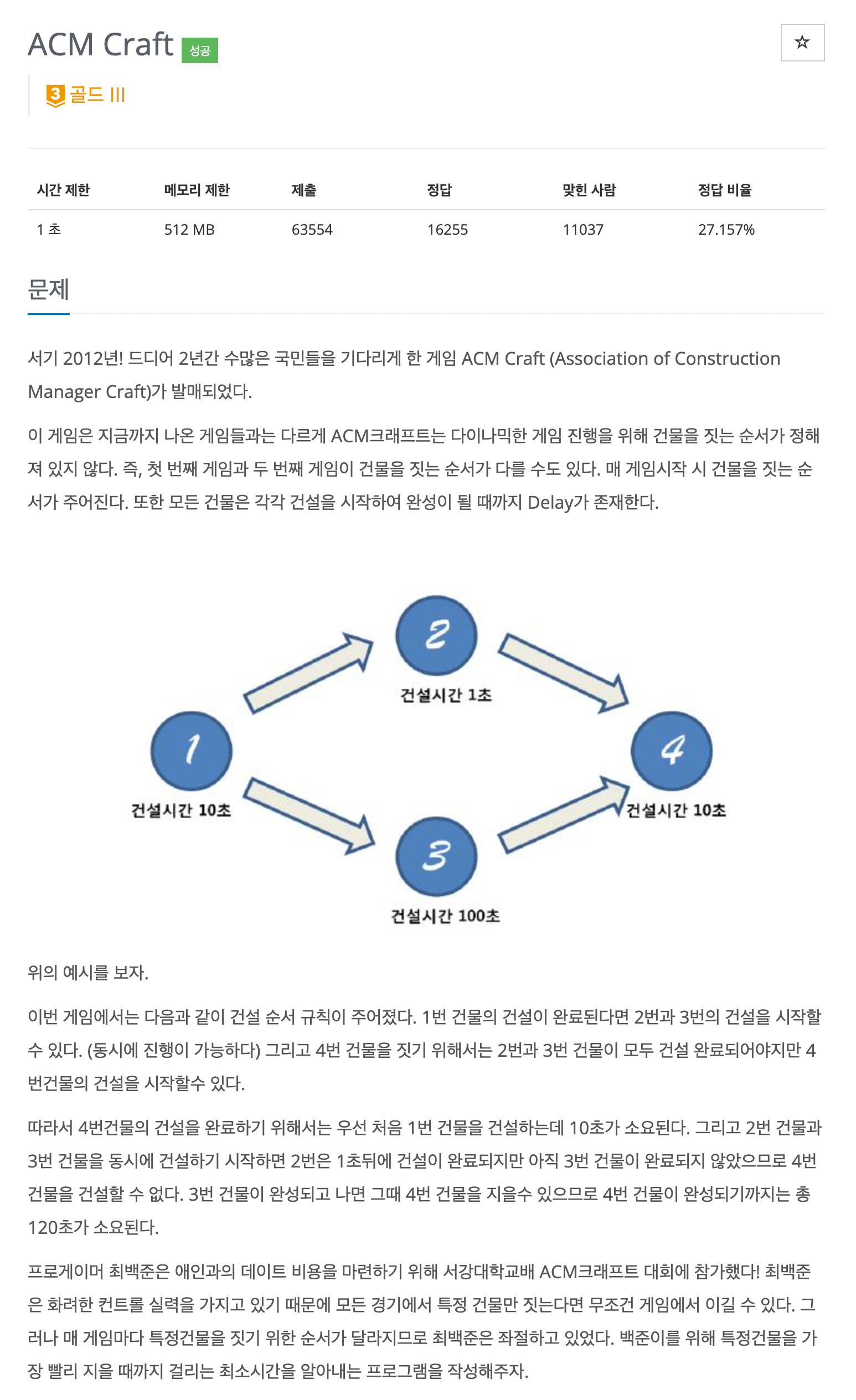
위 문제의 경우 4 건물을 건설하기 위해 2, 3 건물이 선행되어야 한다.
2, 3 건물을 건설하기 위해서는 1 건물이 선행되어야 한다.
→ 선수 관계가 있구나! (위상 정렬)
4를 건설하려면 2와 3이 둘다 건설 완료되어야 하기 때문에 2가 먼저 끝나더라도 3이 끝날때 까지 기다려야 한다.
→ 어느 한 지점에 들어오는 경로가 두 가지 이상이라면 그 경로중 최댓값을 저장해야 한다. (메모이제이션)
📖 위상정렬?
순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘.
ex) 선수과목을 고려한 학습 순서
큐를 이용하는 위상 정렬 알고리즘의 동작 과정 은 다음과 같다.
- 진입차수가 0인 모든 노드를 큐에 넣는다.
- 큐가 빌 때까지 다음의 과정을 반복한다.
- 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 그래프에서 제거한다.
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
🔧 위상 정렬의 특징
- 위상 정렬은 순환하지 않는 방향 그래프에 대해서만 수행할 수 있다.
- 위상 정렬에서는 여러가지 답이 존재할 수 있다. (한 단계에서 큐에 원소가 2개 이상 들어가는 경우)
- 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다.
Python Code
# 백준 1005 ACM Craft
# 위상 정렬
import sys
from collections import deque
read = sys.stdin.readline
def topology_sort(goal):
queue = deque()
# 진입 차수가 0인 모든 노드를 큐에 삽입
for i in range(1, a+1):
if indegree[i] == 0:
queue.append(i)
dp[i] = struct_time[i]
while queue:
current = queue.popleft()
if current == goal:
return dp[current]
# 해당 노드와 연결된 모든 노드들의 진입차수 1 빼기
for next in building[current]:
indegree[next] -= 1
dp[next] = max(dp[next], dp[current] + struct_time[next])
if indegree[next] == 0:
queue.append(next)
# 테스트 케이스 수
T = int(read())
for _ in range(T):
# 건물의 수, 건물 간의 건설 순서 규칙 개수
a, b = map(int,read().split())
building = [ [] for _ in range(a+1) ]
indegree = [0] * (a+1)
struct_time = [-1] + list(map(int,read().split()))
# 해당 건물을 짓는데 걸리는 최소 시간
dp = [0] * (a+1)
# 건설 규칙 저장
for _ in range(b):
x, y = map(int, read().split())
building[x].append(y)
# y 건물의 진입차수 1 증가
indegree[y] += 1
# 승리를 위해 지어야 할 건물
victory = int(read())
print(topology_sort(victory))
# print(dp)
