컴퓨터가 이해하는 정보 단위
비트 (bit)
- 0과 1을 표현하는 가장 작은 정보 단위
- n비트로 2n
- 프로그램은 수많은 비트로 이뤄짐
- 비트보다 더 큰 단위 : 바이트, 킬로바이트, 메가바이트, 기가바이트, 테라바이트 ...
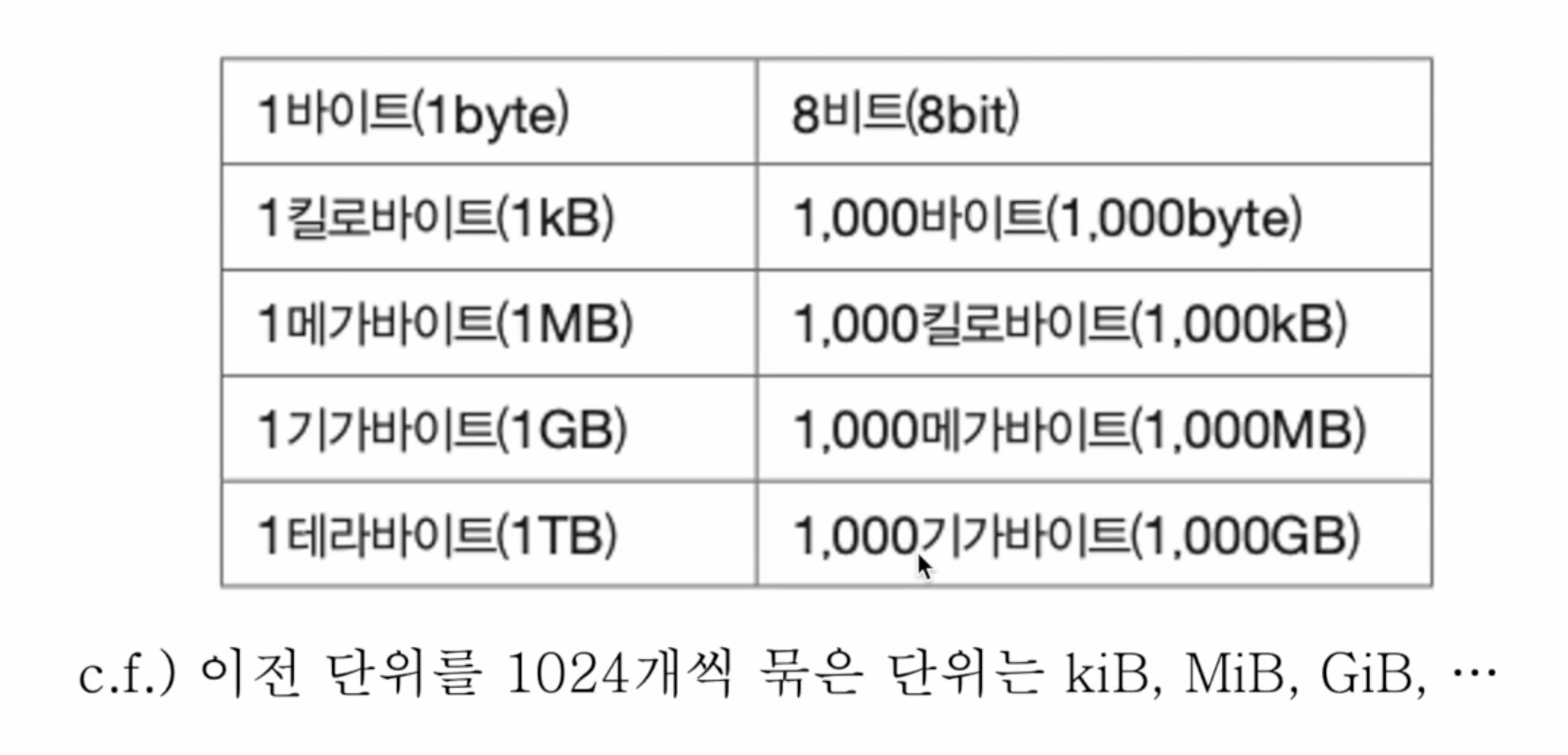
1024개씩 묶는 단위는 따로 있음
워드(word)
- CPU가 한번에 처리할 수 있는 정보의 크기 단위
한번에 처리할 수 있는 크기가 10비트이면 그것은 1워드 - 하프워드 : 워드의 절반 크기
- 풀워드 : 워드 크기
- 더블워드 : 워드의 두배 크기
0과 1로 숫자 표현
0과 1로 숫자 표현하기 (이진법)
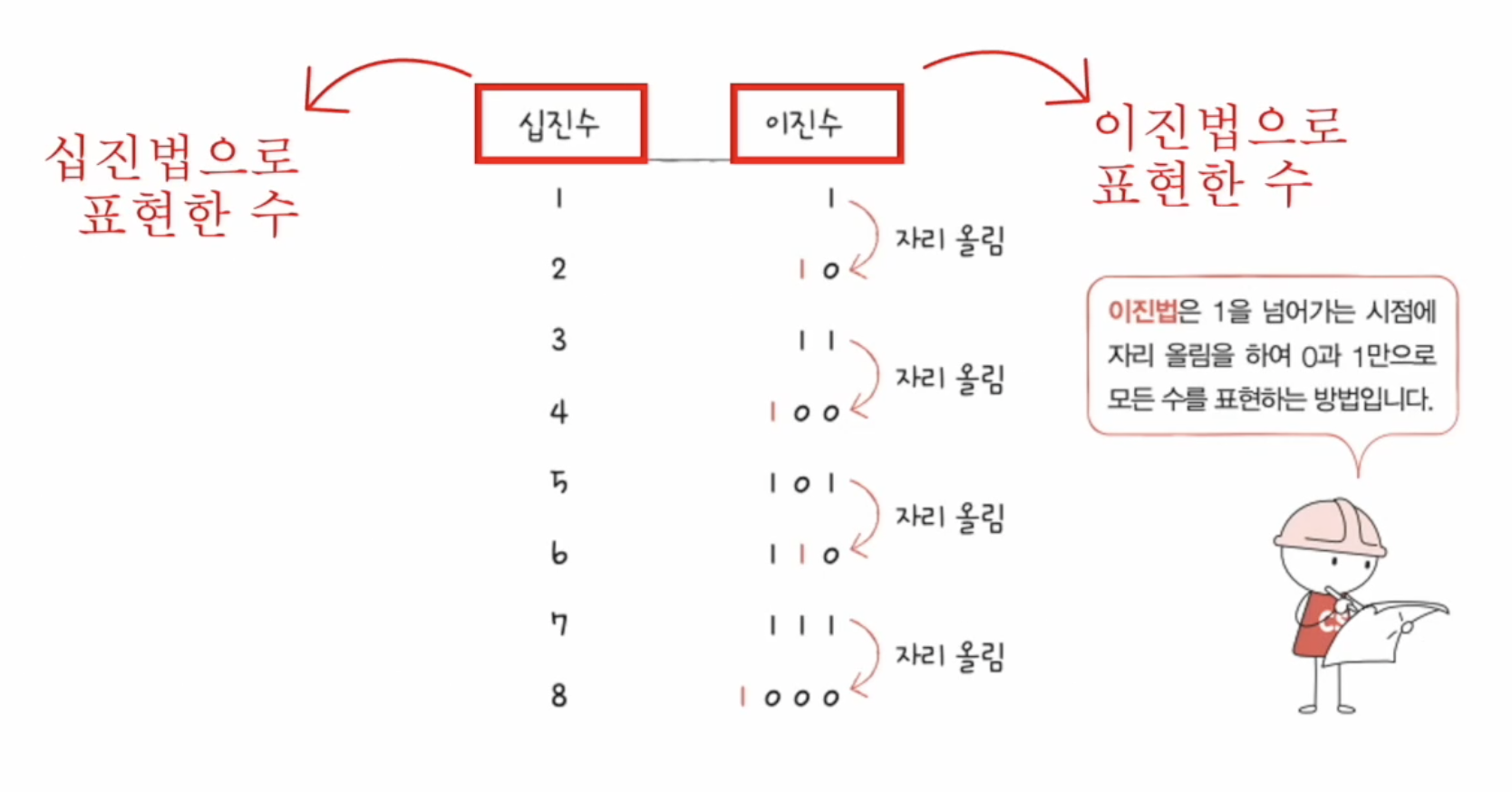
이진법(binary)
- 0과 1로 수를 표현
- 숫자가 1을 넘어가는 시점에 자리를 올림 (이진수)
- 우리가 일상적으로 사용하는 것은 십진법 (9가 넘어갈 때 자리 올림)
- 이진수를 표기할 때에는 아랫첨자 또는 앞에 '0b'를 넣어 표현
- 1000(2) or 0b1000
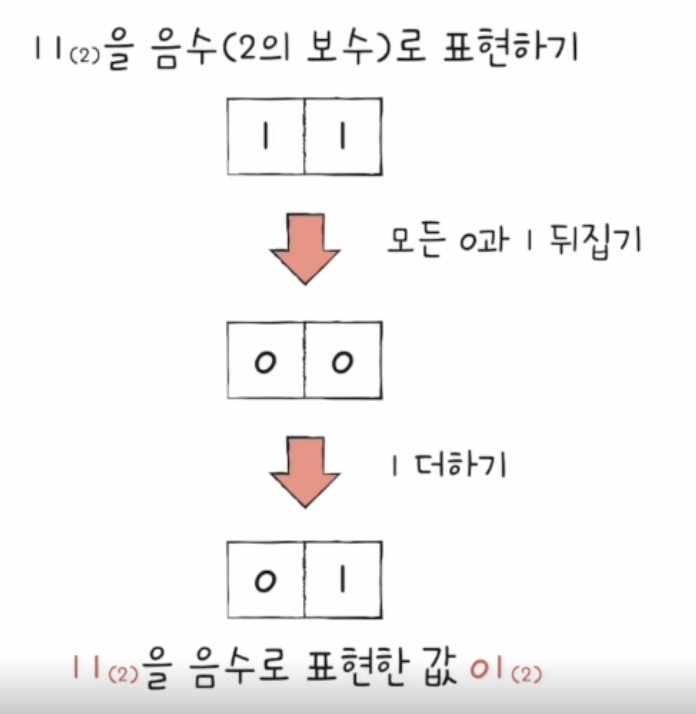
이진법으로 음수 표현
- 2의 보수법
- 어떤 수를 그보다 큰 2n에서 뺀 값
- 즉, 모든 0과 1을 뒤집고 1을 더한 값
- 음수를 양수로 바꿀 때도 모든 0과 1을 뒤집어 1을 더하면 됨
- 음수 양수 구분은 CPU 내부 레지스터에 플래그(flag)가 담당 (플레그 레지스터가 담당)
십육진법
- 이진법으로 숫자가 너무 길어질 때
- 십진수 32 == 이진수 100000 이럴 때 사용
- 십육진법은 수가 15를 넘어가는 시점에 자리 올림
- 표기할 때에는 아랫첨자 또는 앞에 '0x'를 넣어 표현
- 15(16)(수학적 표기) or 0x15(코드상 표기)

이진수 -> 십육진수 변환
- 1A2B(16) == 0001101000101011(2)
- 1 : 0001(2)
- A : 1010(2)
- 2 : 0010(2)
- B : 1011(2)
십육진수 -> 이진수 변환
- 11010101(2) == D5(16)
- 1101 : D(16)
- 0101 : 5(16)
0과 1로 문자 표현
문자 집합
- 컴퓨터가 이해할 수 있는 문자 모음
- 문자 집합에 없는 문자는 컴퓨터가 이해하지 못함
인코딩
- 코드화 하는 과정
- 문자를 0과 1로 이루어진 문자 코드로 변환하는 과정
디코딩
- 코드 해석하는 과정
- 0과 1로 표현된 문자 코드를 문자로 변환하는 과정
아스키 코드
- 알파벳, 숫자, 일부 특수문자 및 제어문자(enter ...)
- 7비트로 하나의 문자 표현
- 8비트 중 1비트는 오류 검출을 위해 사용되는 패리티 비트
- 문자에 부여된 값 == Code Point
- 인코딩이 간단함
- 한글을 포함한 다른 언어 문자, 특수문자 표현 불가
- 7비트로 하나의 문자 표현하기 때문에 128개보다 많은 문자 표현 불가
- 언어별 인코딩 방식 등장
한글 인코딩
- 완성형 vs 조합형 인코딩
- 완성형 인코딩방식 : 하나의 단어 자체에 고유코드 부여
- 조합형 인코딩방식 : 자음과 모음 하나하나에 고유코드 부여
EUC-KR
- KS X 1001 KS X 1003 문자집합 기반의 한글 인코딩
- 완성형 인코딩
- 글자 하나당 1바이트
- 2바이트 == 16비트 == 4자리 십육진수
- 2300여개의 한글 표현
- 모든 한글 표현 부족
- 쀏, 뙠, 휔 같은 표현 불가능
언어별로 인코딩을 국가마다 하게 된다면 다국어 지원 프로그램 개발 시 언어별 인코딩 방식을 모두 이해해야 하는 문제 발생
유니코드 문자집합과 utf-8
- 유니코드
- 통일된 문자집합
- 한글, 영어, 화살표 등 특수 문자 심지어 이모티콘도 가능
- 현대 문자 표현에 있어 매우 중요
- 인코딩 방식 : utf-8, utf-16, utf-32, ...
- utf-8
- 가변 길이 인코딩 : 결과가 1바이트~4바이트
- 인코딩 결과가 몇바이트가 될지는 유니코드에 부여된 값에 따라 다름
- 유니코드에 부여된 값 == 유니코드 코드포인트
