문제
도현이의 집 N개가 수직선 위에 있다. 각각의 집의 좌표는 x1, ..., xN이고, 집 여러개가 같은 좌표를 가지는 일은 없다.
도현이는 언제 어디서나 와이파이를 즐기기 위해서 집에 공유기 C개를 설치하려고 한다. 최대한 많은 곳에서 와이파이를 사용하려고 하기 때문에, 한 집에는 공유기를 하나만 설치할 수 있고, 가장 인접한 두 공유기 사이의 거리를 가능한 크게 하여 설치하려고 한다.
C개의 공유기를 N개의 집에 적당히 설치해서, 가장 인접한 두 공유기 사이의 거리를 최대로 하는 프로그램을 작성하시오.
입력
첫째 줄에 집의 개수 N (2 ≤ N ≤ 200,000)과 공유기의 개수 C (2 ≤ C ≤ N)이 하나 이상의 빈 칸을 사이에 두고 주어진다. 둘째 줄부터 N개의 줄에는 집의 좌표를 나타내는 xi (0 ≤ xi ≤ 1,000,000,000)가 한 줄에 하나씩 주어진다.
출력
첫째 줄에 가장 인접한 두 공유기 사이의 최대 거리를 출력한다.
문제 풀이
기본적으로 이분탐색을 이용해서 최대 거리를 찾는 방식
- 현재 위치가 이전 공유기 설치 위치로부터 일정 거리 이상 떨어져있는지 확인
- 일정 거리 이상 떨어져있다면 설치
- 미만이라면 넘어가기
- 최종적으로 설치된 공유기의 수와 설치해야하는 공유기 수 비교
while (start <= end) {
int mid = (start + end) / 2;
int position = 0; // 공유기 설치 위치
int cnt = 1; // 설치한 공유기 갯수
for (int i = 1; i < n; i++) {
if (houses[i] - houses[position] >= mid) {
// 최소거리보다 크다면 설치
position = i;
cnt++;
}
}
}설치된 공유기의 수가 c보다 작다면?
최소 거리를 늘린다면 설치할 수 있는 공유기의 갯수가 줄어든다.
반대로 최소 거리를 줄인다면 설치 할 수 있는 공유기의 갯수가 늘어난다.
우리는 c개의 공유기 갯수를 맞춰서 설치해야하기 때문에 비교가 필요
if (cnt < c) {
end = mid - 1;
continue;
}
start = mid + 1;예시)
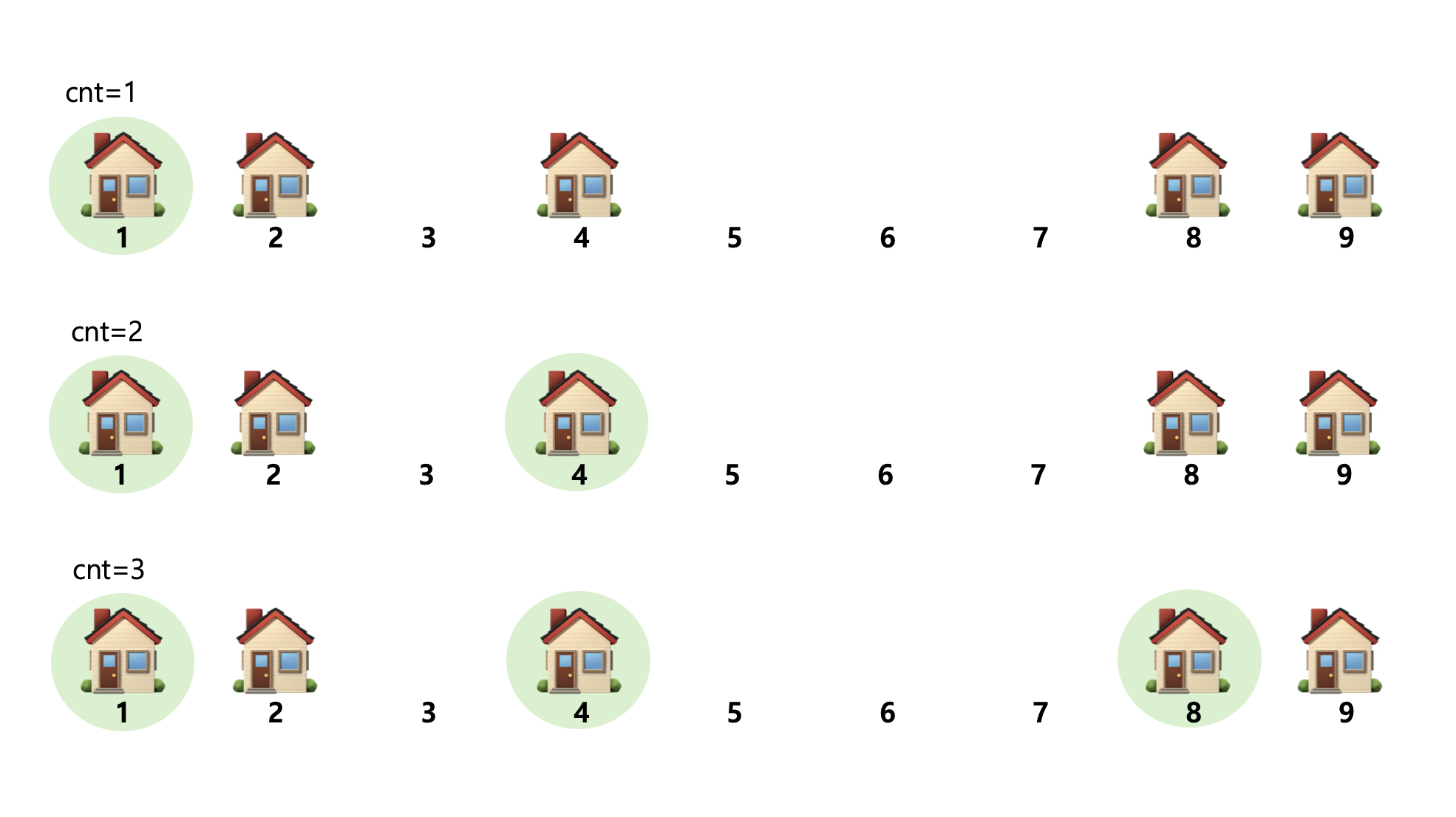
- start = 1: 집과 집 사이가 가질 수 있는 최소거리
end = 9: 집과 집 사이가 가질 수 있는 최대거리
mid = 5
아래의 경우에는 cnt가 c보다 작기 때문에 거리를 좁혀서 더 많은 공유기를 설치할 수 있도록 해야한다.
그렇기 때문에 end의 값을 갱신하도록 한다.
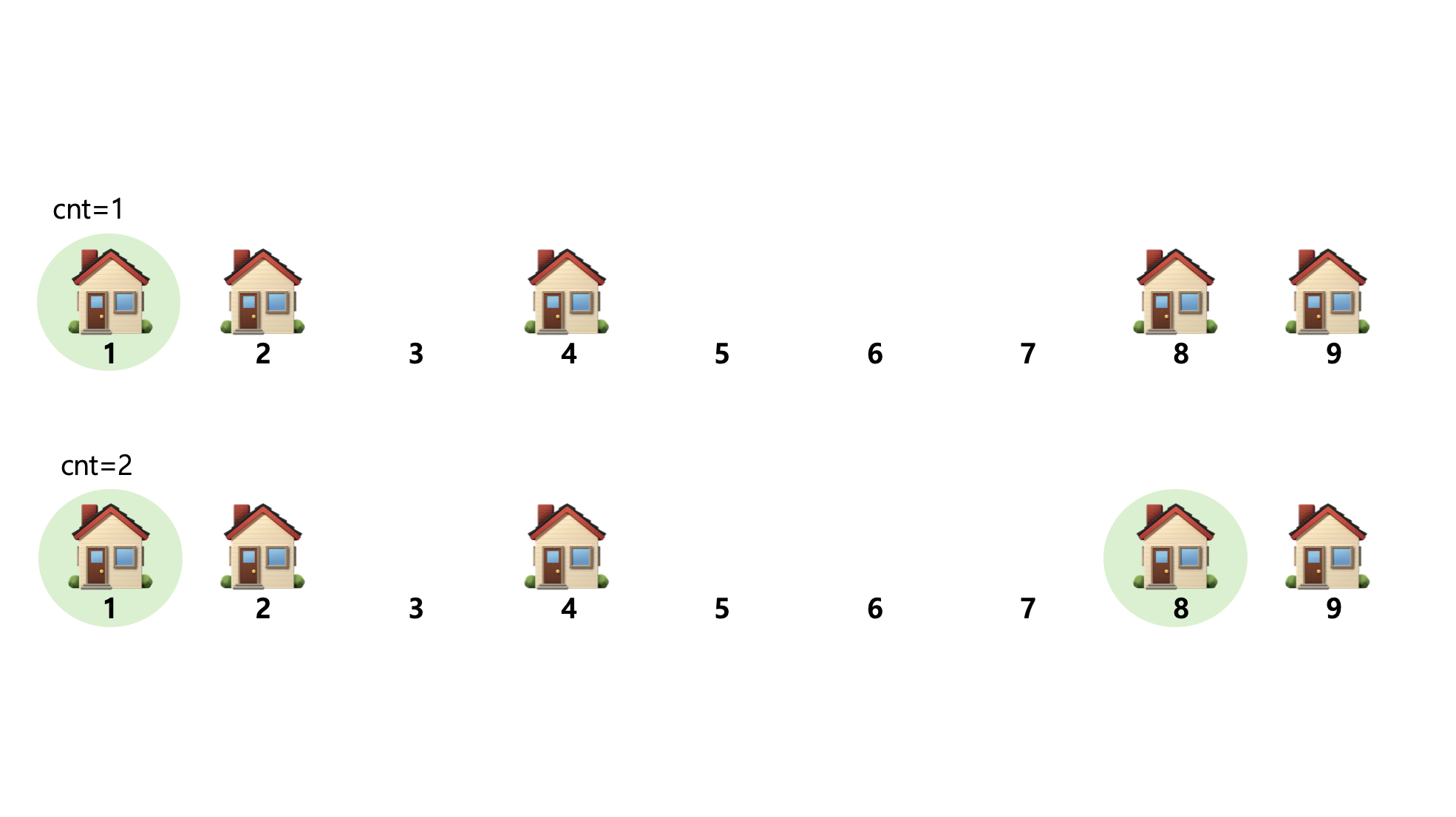
- start = 1
end = 4 (mid -1)
mid = 2 → 최대거리를 구해야하기 때문에 한 번 더 진행
cnt와 c가 동일해지는 거리를 찾았지만 우리가 구해야하는 값은 최대 거리이기때문에 지금 구해진 값이 최대거리임을 확인하기 위해서 계속 진행한다.
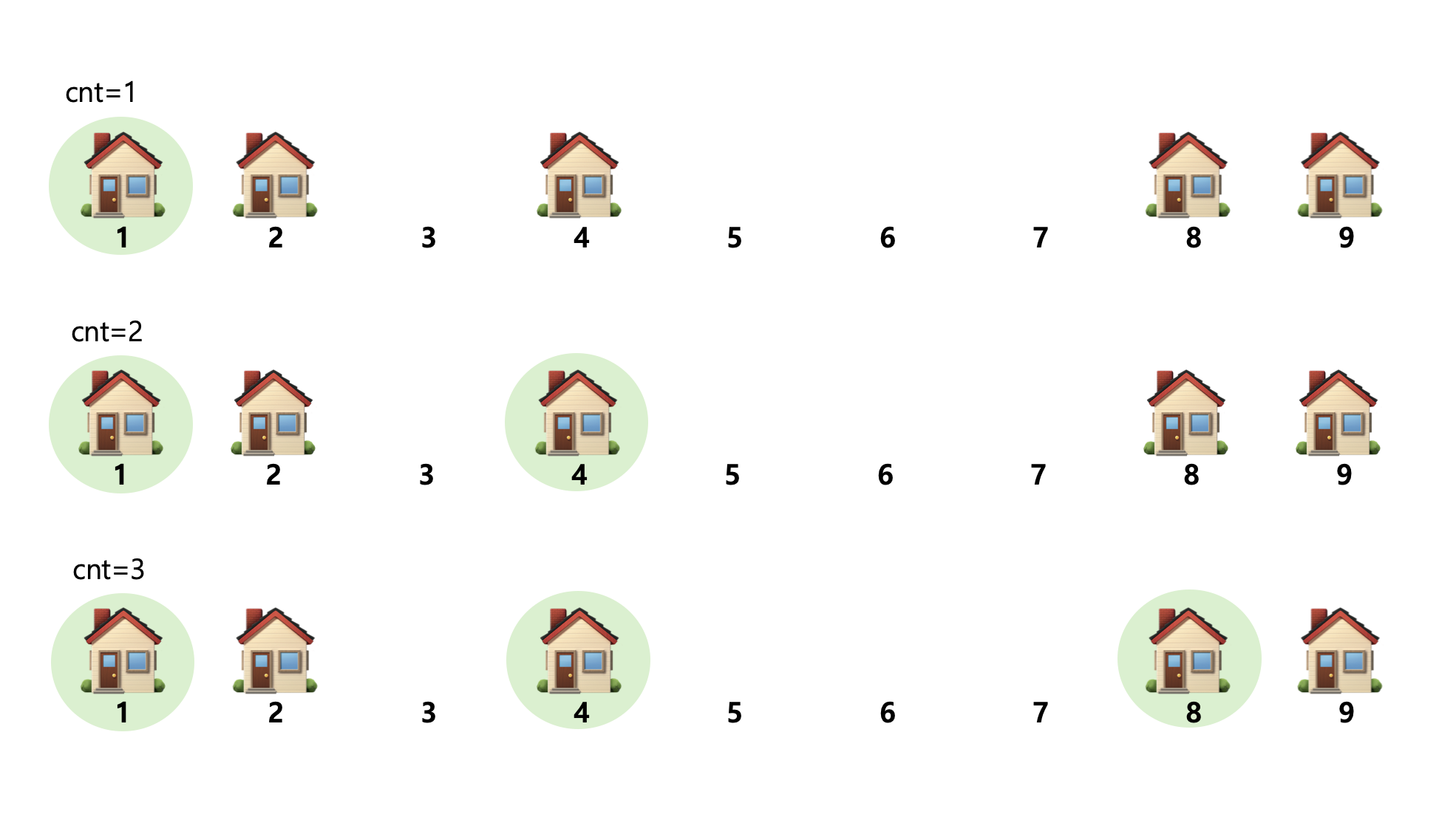
- start = 3 (mid+1)
end = 4
mid = 3
이 과정을 완료하고나면 start ≤ end 라는 while문의 실행 조건을 만족하지 않기 때문에 최대거리가 3임을 알 수 있다.
이때 우리가 구해야하는 최대거리는 cnt == c 인 거리가 여러개 존재할 때, 이 중 최소값을 구해야하는 것이므로 조건을 만족하기 직전의 값을 구해야한다.
전체코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
int[] houses = new int[n];
for (int i = 0; i < n; i++) {
houses[i] = Integer.parseInt(br.readLine());
}
Arrays.sort(houses);
// 공유기 설치 최소 거리를 이분탐색으로
int start = 1;
int end = houses[n - 1];
while (start <= end) {
int mid = (start + end) / 2;
int position = 0; // 공유기 설치 위치
int cnt = 1; // 설치한 공유기
for (int i = 1; i < n; i++) {
if (houses[i] - houses[position] >= mid) {
// 최소거리보다 크다면 설치
position = i;
cnt++;
}
}
if (cnt < c) { // 최소거리인 경우 cnt <= c
end = mid - 1;
continue;
}
start = mid + 1;
}
System.out.println(start - 1);
}
}
매번 느끼지만 이분탐색에서 많이 헤매는 이유는
무엇을 탐색할것인가를 제대로 못정하는 경우가 많아서가 아닐까..
물론 내 얘기다