🪴 십진수를 비트 연산으로 뺄셈
예시
14 - 6단계별 설명
1. 십진수를 이진수로 변환
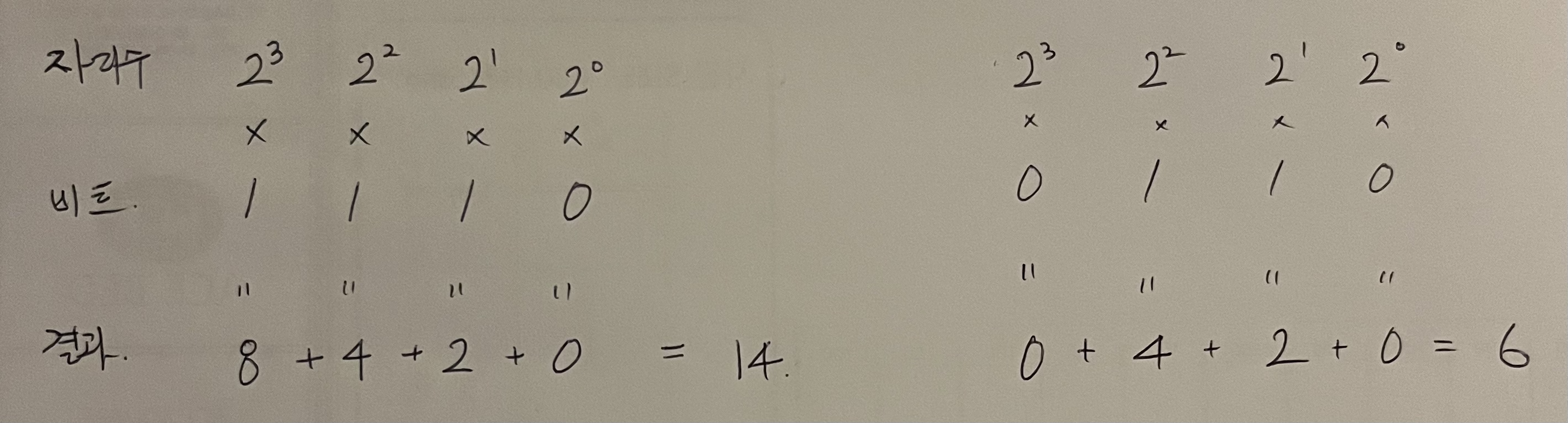
- 14(십진수) -> 1110(이진수)
- 6(십진수) -> 0110(십진수)
2. 6의 '2의 보수' 구하기
- 6의 '1의 보수' -> 1001
- 6의 '2의 보수' -> 1010
3. 14에 6의 '2의 보수' 더하기
1110
+ 1010
-------
110004. 결과 해석
11000은 5비트 이진수이다. 맨 앞의 1은 캐리 비트이므로 무시하고, 나머지 4비트는 1000이다.
따라서, 1000(이진수) -> 8(십진수) 이다.
🪴 비트, 진법, 보수, 캐리 비트
비트
비트(bit, binary digit)는 0 또는 1의 값을 가질 수 있고, 각 참, 거짓 혹은 배타적인 상태를 나타냄.
+) 위의 예시는 4비트
+) 바이트는 비트가 여러 개 모인 것.
진수
컴퓨터는 정수, 실수, 문자를 표현할 수 있음. 하지만 이런 데이터를 계산할 때 n진법을 사용하여 계산을 함. n진법으로 나타낸 수를 n진수 라고 함.
- 2진법: 0~1까지의 2개의 숫자를 사용해서 수를 표현
- 8진법: 0~7 까지의 8개의 숫자를 사용해서 수를 표현
- 16진법: 0~9 까지의 10개의 숫자를 사용하고 남는 자리는 A~F 까지 6개의 문자를 사용해서 수를 표현
+) 위의 예시는 2진수 4비트로 14 - 6 계산, 아래 사진은 2진수 4비트 표
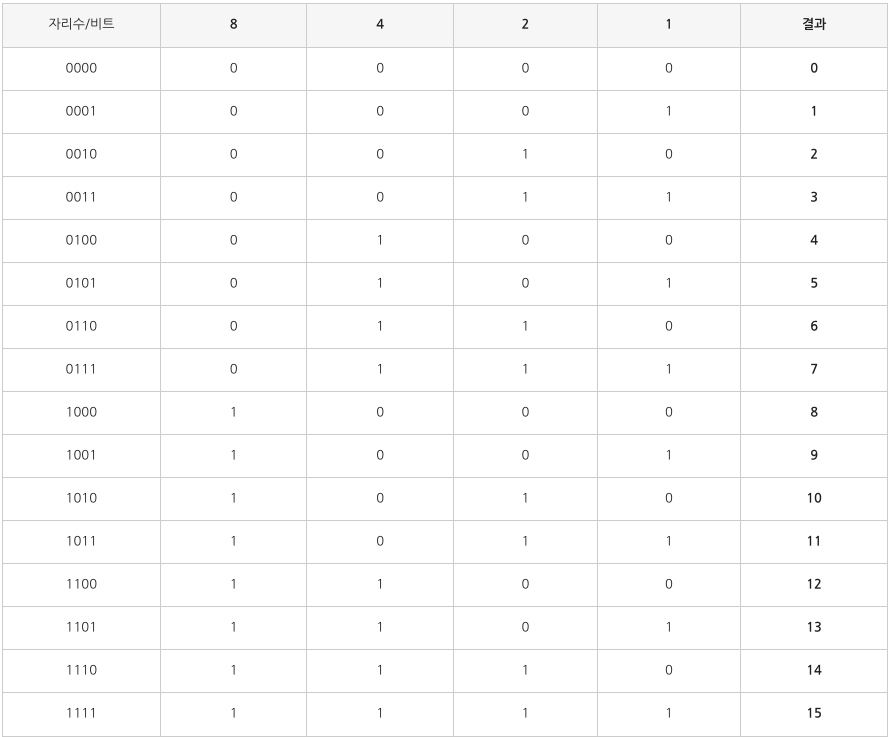
보수
컴퓨터는 가산기임. 뺼셈을 못하고 음수를 더하는 방식으로 계산함. 보수는 컴퓨터에서 음수를 표현하거나, 뺄셈을 더하기 연산으로 처리할 때 사용하는 개념임.
- 1의 보수: 이진수에서 각 비트를 반전시킨 값 (0은 1로, 1은 0으로)
- 2의 보수: 1의 보수에 1을 더한 값 (
1010(이진수)+1(십진수)=1011(이진수))
+) 1의 보수가 아닌 2의 보수를 주로 사용하는 이유는 추가적인 처리가 필요하지 않아 간편하고, 속도가 빠르기 떄문임.
캐리 비트
캐리 비트는 컴퓨터에서 이진수 덧셈을 할 때 자릿수 넘침을 처리하는 비트임. 더할 때 어떤 자리의 결과가 두자리 수가 되면, 더 큰 자리에 1을 "캐리" 해야 함. 이 과정에서 발생하는 비트를 캐리 비트라고 함.
=> 위의 예시에서, 14 - 6 = 8 을 비트연산으로 나타내면
1110
+ 1010
-------
110004비트 범위 끼리 숫자를 더할 때 5비트 결과가 나오는 경우, 그 추가된 1비트가 바로 캐리 비트임.
n비트를 넘어서는 추가적인 캐리 비트는 연산에 필요한 범위를 초과한 값이기 때문에, 결과에서 제외함.
+) 컴퓨터의 메모리나 레지스터가 특정 비트 크기로 제한되어 있기 때문에 범위 벗어난 캐리 비트 무시
+) 메모리: 메모리는 기본적으로 0과 1로 이루어진 이진수로 데이터를 저장하며, 메모리의 각 공간에는 정해진 크기(비트 수)만큼의 데이터를 저장할 수 있음.
+) 레지스터: CPU 내에서 계산을 수행하는데 사용되는 아주 빠른 작은 메모리이며, 정해진 비트 크기로 데이터를 처리
참고 포스트
