세그먼트 트리란

point update와 range query를 모두 O(logN)의 시간에 처리할 수 있는 자료구조입니다.
구간 합을 구할 때
배열 int a[5] = { 5, -1, 3, 2, -8 };가 있을 때 구간 합을 구하려면 O(N)의 시간 복잡도가 필요하다. 이를 방지하지 위해 dp를 이용하여 메모리를 더 사용해 구간합에 O(1)에 접근할 수 있는 방법을 사용한다. 하지만 이렇게 dp를 이용하면 update가 됐을 시에 dp테이블을 O(N^2) 시간 복잡도를 이용하여 변경하여야 한다.
세그먼트 트리는 update와 query연산을 O(logN)에 수행할 수 있다.

세그먼트 트리 구조

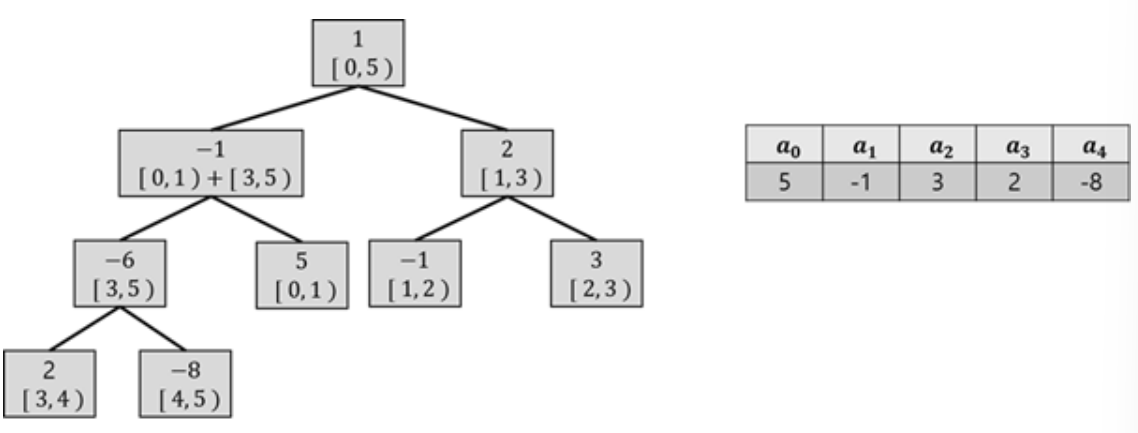
0번 노드는 버리고, 1번 노드가 루트가 되는 방식으로 구현하면 완전 이진 트리의 모습을 하며, 필요한 배열의 길이는 2N이 되고, 리프 노드의 인덱스는 [ N , 2N )입니다.

세그먼트 트리 배열 구현

#include <iostream>
using namespace std;

constexpr size_t n = 5;
int a[n] = { 5, -1, 3, 2, -8 };
int segtree[2 * n]; // 필요한 배열의 길이는 2N입니다.
                    // 리프 노드의 인덱스는 [N, 2N)입니다.
void init() { // 세그먼트 트리 초기화하는 함수
    for (size_t i = 0; i < n; i++) {
        segtree[i + n] = a[i]; // [N, 2N)은 리프노드로 채웁니다.
    }
    for (size_t i = n - 1; i != 0; i--) {// 리프노드가 아닌 노드들을 
        segtree[i] = segtree[i << 1] + segtree[i << 1 | 1]; // 왼쪽 자식+오른쪽 자식 = 부모 로 저장합니다.
    }
}

void update(size_t i, int x){ // i번째 값을 x로 바꿉니다.
    segtree[i + n] = x;
    i = i + n;
    while (i >>= 1) {
        segtree[i] = segtree[i << 1] + segtree[i << 1 | 1];
        // 바꾼 값을 기준으로 위로 올라가며 조상노드를 바꿔줍니다.
    }
}

int query(size_t l, size_t r) {
    int result = 0;
    for (l += n, r += n; l != r; l >>= 1, r >>= 1) {
        if (l & 1)result += segtree[l++]; // l이 오른쪽 노드이면 더해주고 올립니다.
        if (r & 1)result += segtree[--r]; // r이 오른쪽 노드이면 빼주고 더합니다.
    }
    return result;
}

int main(void) {
    init();
    update(1, 100);
    cout << query(1, 4);
    return 0;
}