부분집합의 포함 여부
집합 {1, 2, 3}의 원소에 대해 각 부분집합에서의 포함 여부를 트리로 표현
def f(i, k, key):
if i == k: # 내가 k에 접근하려고 하면 (배열 모든 원소에 접근하려고 하면), 하나의 부분집합 완성
s = 0
for j in range(k):
if bit[j]:
if bit[j]:
s += A[j] # 부분집합의 합
if s == key:
return 1
return 0
# if s == key: # 합이 key 와 같은 부분집합
# for j in range(k):
# if [bit]j:
# print(A[j], end = ' ')
# print()
else:
bit[i] = 1 # A[i] 에서 할일
if f(i + 1, k, key):
return 1
bit[i] = 0
if f(i + 1, k, key): # 갈림길이 2개면 2번의 재귀호출
return 1
return 0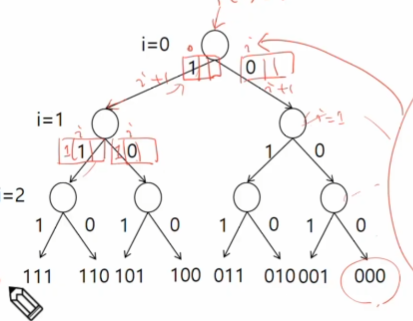
1 넣고 아래 자리로 단계로 가서 1, 1 / 1, 0 이런 방식으로 작동
부분집합의 합
단순히 합만 필요로하는 경우에는 비트를 만들 필요가 없다
위 매단계마다 비트 배열을 읽어서 합을 더하는 것은 가치지기 안하는 것
부분집합 합을 보면 찾고자 하는 합보다 크면 남은 집합 고려할 필요 없다, 가지치기
def f(i, k, s, t): # i원소, k집합의 크기, s i-1까지 고려된 합
global = cnt
global = fcmt
fcmt += 1
if s > t: # 고려한 원소의 합이 찾는 합보다 큰 경우 (함수 호출 수가 줄게된다) (이게 없으면 모든 경우 다 뒤짐)
return
elif s == t: # 내가 찾는 목표에 도달했을 때 (남은원소 있거나 없거나)
cnt += 1
return # 나머지 고려할 필요 없어
elif i == k: # 너 마지막 원소인데?, 모든원소 고려
return
# if s == t:
# for j in range(k):
# if [bit]j:
# print(A[j], end=" ")
# print()
# cnt += 1
return
else:
bit[i] = 1 # bit i를 1로 만들었다
f(i + 1, k, s+A[i], t) # A[i] 포함, 이전까지 포함된 합 s에 내가 포함하기로 한 애를 더해서 넘겨줄게
bit[i] = 0
f(i + 1, k, s, t) # A[i] 미포함
A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
N = len(A)
key = 10
cnt = 10
bit = [0] * N
fcnt = 0
f(0, N, 0, key)
print(cnt, fcnt) # 합이 key인 부분집합의 수그냥 부분집합의 합만 계산
1 -> 3(+2) / 1(+0)
0 -> 2(+2) / 0(+0)
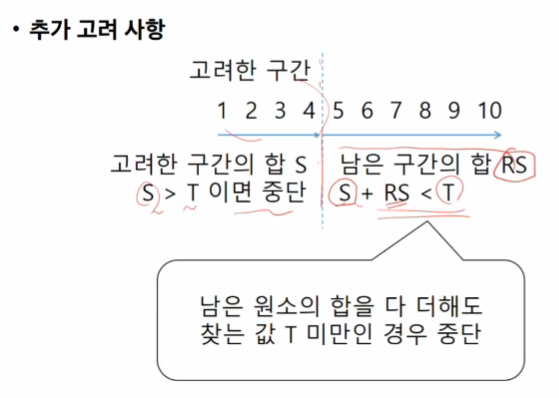
남은 구간의 합을 어떻게 매번 구하지?
앞 고려한 구간을 전체에서 뺀다 (전체 - 고려한 구간 - 뒷 원소부터 차례로 빼간다(-4, -3, ...))
순열
A[1, 2, 3]의 모든 원소를 사용한 순열
- 총 6가지 경우
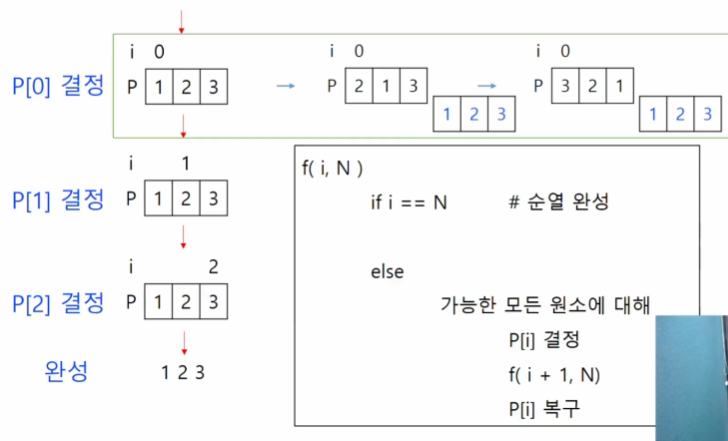
f(i, N)
if i == N #순열 완성
else
# 가능한 모든 원소에 대해 P[i] 결정
f(i + 1, N)
P[i] 복구 (원본으로 만들어 놓고 다시 옆에 꺼랑 바꿈)def f(i, k):
if i == k:
print(p)
else:
for j in range(i, k):
p[i], p[j] = p[j], p[i] # 자리를 교환해봐
f(i + 1, k)
p[i], p[j] = p[j], p[i] # 원상복귀 해주는 부분이 없으면 중복이 생김
p = [1, 2, 3]
N = len(p)
f(0, N)분할 정복 알고리즘
설계 전략
- 분할: 작은 부분으로 나눈다
- 정복: 나눈 작은 문제를 각각 해결한다
- 통합: (필요하다면) 해결된 해답 모은다
분할정복 예제
- 거듭제곱
C의 n 제곱

- 분할 정복 기반의 알고리즘 : O(로그 n)
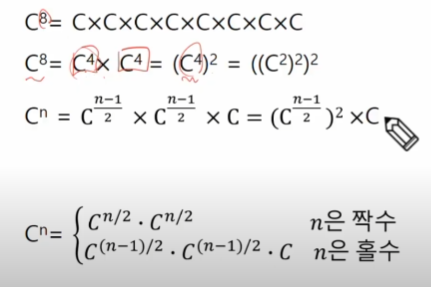

퀵 정렬
주어진 배열을 두 개로 분할하고, 각각을 정렬
- 다른점: 합병 정렬은 그냥 두 부분으로 나누는 반면에, 퀵정렬은 분할할 때 기준아이템 중심으로 작은 것은 왼편, 큰 것은 오른편에 위치시킨다
- 다른점2: 각 부분 정렬이 끝난 후, 합병정렬은 "합병"이란 후처리 작업이 필요하나, 퀵정렬은 필요로 하지 않는다
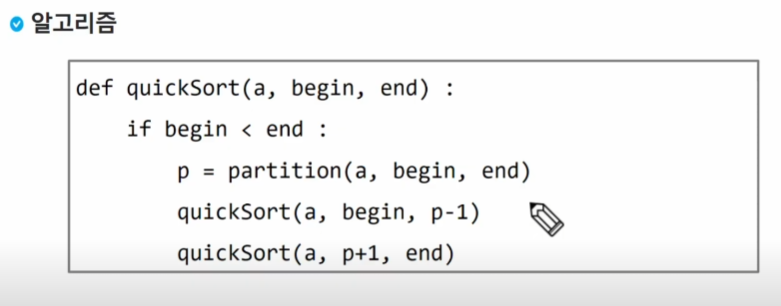
퀵 정렬 수행 과정
- 예제: 69, 10, 30, 2, 16, 8, 31, 22
원소 개수가 8개이므로 네 번째 자리에 있는 원소 2를 첫 번째 피봇으로 선택하고 퀵 정렬 시작

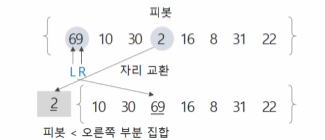
피봇 왼쪽은 공집합, 오른쪽은 피봇보다 큰 애들만 몰려있게 된다
피봇 오른쪽에 큰 애들 모아놓고 왼쪽엔 작은애들 모아놓으려고 하는 것
- 피봇은 기준값, 한번 피봇 결정되었던 애는 한번 돌아가고 나면 자기자리를 찾는다
