어떻게 풀기 고민하는 단계에서 다음과 같은 생각을 했다.
Greedy - 가장 연결이 많이 된 노드부터 하나씩 선택
연결된 노드의 수가 같은 경우 선택 기준이 애매하다.
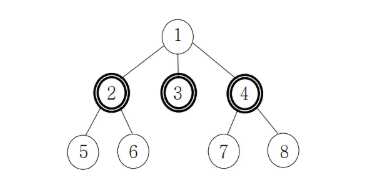
예제 1번과 같은 경우 1, 2, 4번 노드가 모두 연결된 노드가 3개다. 위 예제에서는 1, 2, 4 모두 선택을 해도 3이 되긴 하지만 노드의 개수가 더 많아지는 경우에 반례가 생길것 같아서 일단 pass
생각해보니 어떤 선택이 다음 선택에 영향을 미치는 것 같다.. 그렇다면 dp를 고려해보자.
Dp
dp를 쓰면 되지 않을까? 어떤 노드가 얼리어답터인 경우와 그렇지 않은 경우로 구분하자.
dp[고려중인 노드][얼리어답터 여부] = 최소 비용으로 하면 될 거 같았다.
특정 노드가 얼리어답터라면 그 노드의 자식들은 뭐가 와도 상관이 없고, 얼리어답터가 아니라면 그 노드의 자식들은 모두 얼리어답터여야 한다.
점화식을 세워본다면
이를 코드로 표현하면
#include<iostream>
#include<vector>
#include<queue>
#include<cmath>
using namespace std;
int N;
vector<vector<int>> nextNodes(1'000'001);
bool visited[1'000'001];
int dp[1'000'001][2];
void make_dp(int cur){
dp[cur][1] = 1;
visited[cur] = true;
for(int next : nextNodes[cur]){
if(visited[next]) continue;
make_dp(next);
dp[cur][0] += dp[next][1];
dp[cur][1] += min(dp[next][0], dp[next][1]);
}
}
int main(){
cin >> N;
for(int i = 0; i < N-1;i++){
int a, b;
cin >> a >> b;
nextNodes[a].push_back(b);
nextNodes[b].push_back(a);
}
make_dp(1);
cout << min(dp[1][0], dp[1][1]) << endl;
return 0;
}dp문제는 점화식만 잘 세우면 쉽지만 점화식을 세우는게 어려운 것 같다..
